
- •Ограниченные числовые множества. Существование точных граней.
- •Предел числовой последовательности.
- •Существование предела последовательности.
- •Предел функции в точке.
- •Основные теоремы о пределах.
- •Непрерывность функции в точке. Свойства непрерывных функций.
- •Дифференцируемость функции в точке. Производная и дифференциал.
- •Основные теоремы дифференциального исчисления.
- •Приложения дифференциального исчисления к исследованию ф-ции.
- •Интеграл Римана и его свойства.
- •Приложения интеграла Римана.
- •Дифференцирование функций многих переменных.
- •Основные теоремы о дифференцировании функций многих переменных.
- •Числовые ряды.
- •Функциональные последовательности.
- •Функциональные ряды.
- •Тройной интеграл.
- •Двойной интеграл.
- •Теорема о существовании и единственности решения задачи Коши для обыкновенного ду первого порядка.
- •Обыкновенные дифференциальные уравнения первого порядка, интегрируемые в квадратурах.
- •Основные свойства решений линейных дифференциальных уравнений. Линейные дифференциальные уравнения с постоянными коэффициентами.
- •Множества, измеримые по Лебегу на прямой. Их свойства.
- •Сравнение интеграла Римана с интегралом Лебега.
- •Дифференцируемость функции комплексной переменной (фкп).
- •Интеграл от функции комплексной переменной.
- •Группы. Примеры групп. Простейшие свойства группы. Подгруппы. Гомоморфизмы и изоморфизмы групп.
- •Кольцо. Примеры колец. Простейшие свойства кольца. Подкольцо. Гомоморфизмы и изоморфизмы колец.
- •Поле. Простейшие свойства поля. Поле q. Поле с.
- •Векторное пространство. Базис и размерность конечномерного векторного пространства. Подпространства. Линейные многообразия. Изоморфизмы векторных пространств.
- •Многочлены от одной переменной над полем. Производная многочленов. Нод двух многочленов и алгоритм Евклида. Неприводимые многочлены.
- •Многочлены над полями с, r и q. Многочлены от n переменных. Алгебраические и трансцендентные числа.
- •Отношение делимости в кольце целых чисел.
- •Отношение сравнения в кольце целых чисел.
- •Аксиоматические теории и схема их построения. Построение системы натуральных чисел.
- •Построение системы целых чисел. Операции на множестве целых чисел и их свойства. Система рациональных чисел.
- •Плоскость Лобачевского. Аксиома Лобачевского. Аксиома Лобачевского и простейшие следствия из нее. Взаимное расположение прямых на плоскости Лобачевского.
- •Трехмерное евклидово пространство. Векторное произведение векторов. П риложения к решению задач.
- •Взаимное расположение двух плоскостей, прямой и плоскости, двух прямых в трехмерном пространстве.
- •Трехмерное евклидово пространство. Смешанное произведение векторов. Приложения к решению задач.
- •Полярные координаты. Простейшие задачи в полярных координатах. Уравнение линии. Эллипс, гипербола и парабола в полярных координатах.
- •Проективная плоскость и ее модели. Проективные свойства фигур. Группа проективных преобразований плоскости. Приложения к решению задач.
- •Параллельное проектирование и его свойства. Изображение плоских и пространственных фигур в параллельной проекции. Позиционные задачи.
- •Графы. Виды графов, способы их задания. Числовые характеристики графов.
- •Основные понятия и формулы комбинаторики.
- •Элементы логики высказ, математической логики и логики предикатов.
- •Бинарное отношение. Отображения, обратное отображение. Отношения эквивалентности и порядка. Фактор–множество.
- •Кривые в трёхмерном евклидовом пространстве. Касательная, нормальная и соприкасающаяся плоскость кривой. Канонический репер кривой. Кривизна и кручение кривой.
- •Поверхности в трёхмерном евклидовом пространстве. Касательная плоскость и нормаль к поверхности. Первая и вторая квадратичные формы поверхности и их применение.
- •Методы научного познания в обучении математике.
- •Методика изучения математических понятий.
- •Методика изучения математических предложений.
- •Задачи в школьном курсе математики.
- •Методика изучения числовых множеств в школьном курсе математики.
- •Методика изучения тождественных преобразований выражений в школьном курсе математики.
- •Понятие функции. Методика изучения алгебраических функций в школьном курсе математики. Функции натурального аргумента.
- •Методика изучения трансцендентных функций в школьном курсе.
- •Методика изучения производной. Применение производной в школьном курсе математики.
- •Методика решения трансцендентных уравнений, неравенств и их систем.
- •1.Тригонометрические уравнения. Содержание и методика.
- •Методика изучения начал систематического школьного курса планиметрии.
- •Методика изучения четырехугольников, их свойств.
- •Методика изучения величин в школьном курсе планиметрии.
- •Методика изучения основных соотношений между элементами треугольника.
- •Методика изучения подобия фигур.
- •Методика формирования у учащихся навыков решения задач по планиметрии. Обучение школьников решению задач на построение циркулем и линейкой.
- •Методика изучения первых разделов систематического курса стереометрии. Особенности методики работы с многогранниками.
- •Методика изучения взаимного расположения прямых и плоскостей в пространстве.
- •Методика обучения учащихся нахождению углов и расстояний в пространстве.
- •Методика изучения многогранников и их свойств.
- •Методика изучения тел вращения, их св-в.
- •Методика изучения площадей поверхностей и объемов многогранников и тел вращения.
- •Методика обучения школьников решению задач на комбинации многогранников и тел вращения.
Понятие функции. Методика изучения алгебраических функций в школьном курсе математики. Функции натурального аргумента.
Function – исполнение, совершение. Введено нем. мат-ом Лейбницем в 17 в., но понятие рассм-ся им в более узком смысле, т.к. связывалось с геом. образом, т.е. графиком ф-ий.
В научно-метод. лит-ре выделяют 2 подхода к введению понятия ф-я: 1)классический, связан с понятием переменной величины; 2)современный, ф-я отождествляется с понятием отображения и опр-ся как соотв-ие между 2-мя мн-ми. В дейчтвующих учебниках ф-я опред-ся след. образом: Кузнецова: з-н по которому каждому значению переменной x из некот. мн-ва чисел D ставится в соотв-ие одно определённое значение переменной y, назыв-ся ф-ей заданной на этом мн-ве D; Латотин: зависимость одной переменной от другой при кот. каждому значению переменной x из определённого мн-ва D соотв-ет единств. знач. переменной y наз-ся функцион-ой зависимостью или ф-ей. Методическая схема изучения ф-ий в базовой школе: 1)анализ конкр. Задачи или пример из реальной жизни, приводящий к данной ф-и(убедить учеников в целесообразности изучения данной ф-и на уроках мат-ки); 2)опр-ие, запись с пом. ф-лы, исследование параметров входящих в ф-лу; 3)рассм-ие ф-и с конкр. данными и составление таблицы; 4)построение графика по точкам; 5)исследование св-в ф-и с пом. графич-го представления; 6)установление влияния параметров на хар-р графического изображения; 7)формулировка св-в для ф-и заданной в общем виде и д-во их; 8)обучение истолкование св-в ф-и на 3-х языках(графич-ом, словесном, символическом); 9)применение знаний к решению задач. ОСОБЕННОСТИ ИЗУЧЕНИЯ РАЗЛИЧНЫХ ВИДОВ Ф-Й: 1.не всегда мотивируется введение частных видов ф-и.2.сущ-ет 2 подхода к форм-ке опр-ния:
А)ф-я,заданная
формулой…(К.).Б) ф-я,кот.может быть задана
формулой…(Л.)Например,
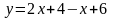 не
явл. линейной по К., но явл. по Л.3.не
поясняется, что соединение отмечнных
точек неправомерно,уч-мся сообщается,
что в силу ограниченности выбора точек
мы соединяем полученные точки непрерывной
линией.4.Не
всегда уделяется внимание воспитанию
графической культуры школьников:-
правильное изображение системы координат;
– буквы не пересекают линии; – правильное
чтение графиков; –матем-ая речь.
5.различен
порядок изучения ф-й: К.:
не
явл. линейной по К., но явл. по Л.3.не
поясняется, что соединение отмечнных
точек неправомерно,уч-мся сообщается,
что в силу ограниченности выбора точек
мы соединяем полученные точки непрерывной
линией.4.Не
всегда уделяется внимание воспитанию
графической культуры школьников:-
правильное изображение системы координат;
– буквы не пересекают линии; – правильное
чтение графиков; –матем-ая речь.
5.различен
порядок изучения ф-й: К.:
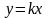

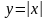
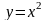
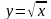
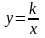 ,
квадрат.ф-я. Л:
,
квадрат.ф-я. Л:

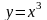
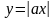 ,квадрат.ф-я.
6.В
уч-ке К.
подчеркивается, что ф-й без обл.опр-ния
не бывает и обл.опр-ния должна входить
в формулировку опр-ния ф-и, поэтому
бессмысленно задания найти обл.опр-ния
ф-и. 7.Отдельные
авторы проводят частичное исследование
ф-й до построения таблицы. 8.
Понятие четной и нечетной ф-и по программе
вводится лишь в 11 кл. Учителю полезно
после форм-ки опр-ний: –четно выделить
2 требования(обл.опр-ния отн-но нуля
симметрична, вып-ся рав-во f(-x)=-f(x)
или f(-x)=f(x).
–сформулировать отрицание данного
опр-ния: ф-я не явл. четной или нечетной,
если не вып-ся хотя бы одно из 2-х
требований)
,квадрат.ф-я.
6.В
уч-ке К.
подчеркивается, что ф-й без обл.опр-ния
не бывает и обл.опр-ния должна входить
в формулировку опр-ния ф-и, поэтому
бессмысленно задания найти обл.опр-ния
ф-и. 7.Отдельные
авторы проводят частичное исследование
ф-й до построения таблицы. 8.
Понятие четной и нечетной ф-и по программе
вводится лишь в 11 кл. Учителю полезно
после форм-ки опр-ний: –четно выделить
2 требования(обл.опр-ния отн-но нуля
симметрична, вып-ся рав-во f(-x)=-f(x)
или f(-x)=f(x).
–сформулировать отрицание данного
опр-ния: ф-я не явл. четной или нечетной,
если не вып-ся хотя бы одно из 2-х
требований)
Методика изучения трансцендентных функций в школьном курсе.
Тригоном-ие
ф-и: В учебнике
К. нет четкого разделения между
исследованием функции и построением
графика. В главе предшествующей изучению
триг.функций - «триг. выражения» авторы
исследуют св-ва выражений
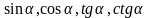 с помощью ед.окружности, а при изучении
свойств триг. Функций на них ссылаются.
Определение триг. функций вводится
след.образом: функция
синус –
ф-ция, заданная формулой
с помощью ед.окружности, а при изучении
свойств триг. Функций на них ссылаются.
Определение триг. функций вводится
след.образом: функция
синус –
ф-ция, заданная формулой
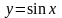 ,
с областью опредления – множество R.
Также косинус. Функция
тангенс –
функция, заданная формулой
,
с областью опредления – множество R.
Также косинус. Функция
тангенс –
функция, заданная формулой
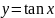 , с областью определения – множеством
действительных чисел
, с областью определения – множеством
действительных чисел
 ..
Функция
котангенс-
функция, заданная формулой
..
Функция
котангенс-
функция, заданная формулой
 ,
с областью определения – множеством
действительных чисел
,
с областью определения – множеством
действительных чисел
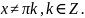 Определение не выделено шрифтом, поэтому
полезно записать их ученикам в тетрадь.
Введение
определения не мотивируется.
Пусть x-
действ.число, оно может быть радианной
мерой некот.угла, для кот. однозначно
определено число
Определение не выделено шрифтом, поэтому
полезно записать их ученикам в тетрадь.
Введение
определения не мотивируется.
Пусть x-
действ.число, оно может быть радианной
мерой некот.угла, для кот. однозначно
определено число
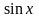 .
Тем самым на мн-ве R
определена ф-я
.
Задача:
построить график. С этой целью автор
предлагает составить табл.значений ф-и
на промежутке от о до
.
Тем самым на мн-ве R
определена ф-я
.
Задача:
построить график. С этой целью автор
предлагает составить табл.значений ф-и
на промежутке от о до
 .(с
точностью до 0,1 через
.(с
точностью до 0,1 через
 ),
а затем построить часть графика, и
используя периодичность – весь график,
при этом делают замечание, ч то можно
было бы построить график от о до
.(,
а затем использовать нечетность ф-ции.
Свойства
формулируются в виде теоремы
с пом.графика, содержащей 8
свойств:
обл.определения, область значений,
периодичность, наиб.,наим.значения, нули
ф-ции, промежутки знакопостоянства,
четность, нечетность, возрастание,
убывание. Точек пересечения с осями не
находят, т.к. не умеют решать триг.уравнения.
Показательная
ф-ия:
актуализировать знания уч-ся по теме,
кот. непоср-но изучалась перед введением
степ-ой ф-и – степень с рац. показателем,
её св-ва, степень с действит. показателем.
В систему упражнений включит следующие:
1)сравнить
степени с одним основанием; 2)сравнить
степени с одиноковыми основаниями и
сделать вывод. Подвести что каждому t,
ставится одно знач.
),
а затем построить часть графика, и
используя периодичность – весь график,
при этом делают замечание, ч то можно
было бы построить график от о до
.(,
а затем использовать нечетность ф-ции.
Свойства
формулируются в виде теоремы
с пом.графика, содержащей 8
свойств:
обл.определения, область значений,
периодичность, наиб.,наим.значения, нули
ф-ции, промежутки знакопостоянства,
четность, нечетность, возрастание,
убывание. Точек пересечения с осями не
находят, т.к. не умеют решать триг.уравнения.
Показательная
ф-ия:
актуализировать знания уч-ся по теме,
кот. непоср-но изучалась перед введением
степ-ой ф-и – степень с рац. показателем,
её св-ва, степень с действит. показателем.
В систему упражнений включит следующие:
1)сравнить
степени с одним основанием; 2)сравнить
степени с одиноковыми основаниями и
сделать вывод. Подвести что каждому t,
ставится одно знач.
 , следовательно задана функция y=
, следовательно задана функция y=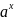 ,
a>0.
Затем обсудить
название функции: Переменная в показатели
степени => показательная.
Потом уточнить знач. входящих эл-тов,
оговорить случай а=0, добавить к определению
а
,
a>0.
Затем обсудить
название функции: Переменная в показатели
степени => показательная.
Потом уточнить знач. входящих эл-тов,
оговорить случай а=0, добавить к определению
а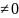 и сформулировать определение.
Опр. Функция,
заданая формулой y=
при a>0,
а
называют показательной.
Обл. определения
показательной функции – это математическая
обл. определения выражения
,
т. е. R.
Далее следует
построить график на доске.
Мотивацию
изучения
данной темы можно ввести на любом моменте
урока, различными примерами: 1)зависимость
популяций сов определяется по закону
y=y
и сформулировать определение.
Опр. Функция,
заданая формулой y=
при a>0,
а
называют показательной.
Обл. определения
показательной функции – это математическая
обл. определения выражения
,
т. е. R.
Далее следует
построить график на доске.
Мотивацию
изучения
данной темы можно ввести на любом моменте
урока, различными примерами: 1)зависимость
популяций сов определяется по закону
y=y ;
2)атмосферное
давление измер по закону p=
;
2)атмосферное
давление измер по закону p=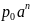 и т. д. Введение
логарифмической функции, 2 подхода: 1)
Вводится понятие
обратной функции; фун., обратная
показательной y=
,
a>0,
а
называется логарифмической, и задаётся
формулой:
и т. д. Введение
логарифмической функции, 2 подхода: 1)
Вводится понятие
обратной функции; фун., обратная
показательной y=
,
a>0,
а
называется логарифмической, и задаётся
формулой:
 ;
2)ввод-ся
опр-ие логарифма, формулируются и док-ся
его св-ва, затем с пом. уч-ся устанавлив-ся,
что каждому значению
;
2)ввод-ся
опр-ие логарифма, формулируются и док-ся
его св-ва, затем с пом. уч-ся устанавлив-ся,
что каждому значению
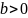 соотв-ет единств. знач.
соотв-ет единств. знач.
 (
(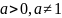 ).
Тем самым задана ф-ия
).
Тем самым задана ф-ия
 ,
кот. наз-ся логарифмической. Мотивация
введения
логарифма явл. след. факторы: 1)необходимость
решения уравнения b=
,
2)в
уч Кузн. Уточнение и практическое
применение некот. св-в показат. ф-и.
Исследование ф-и
провод-ся по общей схеме и формулируются
в виде Т., д-во св-в опирается на св-ва
показат. ф-и. Особенностью исследов.
лог. ф-и явл. д-во утв., что графики показ.
и лог. ф-ий имеющих одинаков. основания,
симметричны отн-но прямой y=x.
,
кот. наз-ся логарифмической. Мотивация
введения
логарифма явл. след. факторы: 1)необходимость
решения уравнения b=
,
2)в
уч Кузн. Уточнение и практическое
применение некот. св-в показат. ф-и.
Исследование ф-и
провод-ся по общей схеме и формулируются
в виде Т., д-во св-в опирается на св-ва
показат. ф-и. Особенностью исследов.
лог. ф-и явл. д-во утв., что графики показ.
и лог. ф-ий имеющих одинаков. основания,
симметричны отн-но прямой y=x.
