2. Основные теоремы о пределах.

Опр.(на языке последовательности) Число А наз. пределом f(x) в точке x₀X, если x₁,x₂,x₃,…x_n,… x₀. Где xi не равны x₀, соответствует последов. Значений ф-ций f(x₁),f(x₂),…f(x_n),…  к одному и тому же числу А.

Опр.(по Каши) Пусть f(x) определена в D(f), которая имеет предельную точку x₀. Число А будем наз. пределом ф-ции f(x) в точке x₀, если 0  0, xD(f), 0<x-x₀<f(x)-A<.

Т.(о единственности предела) Если f(x) имеет в точке x₀ предел А , то этот предел единственный.

Т.(о локальной ограниченности ф-ции) Если f(x) имеет конечный предел АR, то  проколотая U_(x₀) в которой эта фун-я ограничена.

Док-во: limf(x)=AR(xx₀ ): 0  U_(x₀),  xD(f) с проколотой U_(x₀) f(x)-A<0

А-<f(x)<A+. Из последнего нер-ва заключаем, что f(x) ограничена снизу А-, сверху А+.

Т.(предельный переход в нер-ве) Если f(x) и g(x) имеют конечные пределы соответственно A и B, и существует проколотая U_(x₀) из области определения этих ф-ций, где f(x)<g(x), то имеет место нерав-во A  B.

Особый случай в пределе суммы.

Т.(предел суммы) Пусть f(x) имеет конечный предел А в некоторой проколотой U_(а), а ф-ия g(x)-б/б, тогда lim(f(x)+g(x))(xa)=+, -,  взависимости от знака g(x). Кроме этого ф-ия f(x) должна быть ограниченной в проколотой U_(а).

Особый случай в пределе произведения.

Если limf(x)=А(xa ), АR или limg(x)=(xa ), то lim(f(x)*g(x))=(xa )

Особый случай в пределе частного.

Т. Если  limf(x)=А(xa), АR (f(x)- ограничена проколотой окрестностью точки а) и  limg(x)=(xa), то lim =0(xa ).

Т.Если  limg(x)=А(xa ) АR, и  limf(x)= (xa ), то lim =0(xa ).

Т.Если  limf(x)=А(xa ) А , и  limg(x)= 0(xa), то lim = (xa ).

Первый замечательный предел: .

Второй замечательный предел: e.

1. Предел константы равен самой этой константе: с = с.

2. Постоянный множитель можно выносить за знак предела: [ k • f(х)] = k f(х).

3. Предел суммы (разности) ф-ций равен сумме (разности) пределов этих ф-ций:

[ f(х) ± g(х)] = f(х) ± g(x).

4. Предел произвед ф-ций равен произвпределов этих ф-ций: [ f(х) •g(х)] = f(х) • g(x).

5. Предел отношения двух ф-ций равен отношению пределов этих ф-ций, если только предел делителя не равен нулю: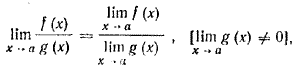

2. Непрерывность функции в точке. Свойства непрерывных функций.

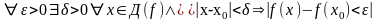Ф-ция y=f(x) наз непр в т Хо прин Д(f), если -\\-\\-\\-, если -\\-\\-\\-, если бесконечно малому приращению аргумента соотвбеск малое приращ ф-ции. Т Хо-это т разрыва ф-ции f(x), т.е. ф-ция не явлнепрерывной. Хо-т разрыва перврго рода, есл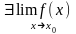и и

1)

2)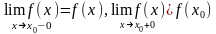 Если 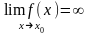или не сущ, то т Хо-т разрыва второго рода.Точкой устранимого разрыва наз.такая точка, что существуетконечный предел т.е новая ф-ция оказалась непрерывной в точке. Глобсв-вами ф-цииназсв-ва, рассм на некотмнож, а лок – в некот окрестности. Локсв-ва: 1)если f(x) непрер в т х=а прин Д(f), то сущ окрестность т а радиуса , в кот f(x) ограничена., т.е. сущ с>0, что |f(x)| c; 2)-\\- и f(a)>0, то сущ окрестность

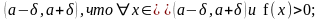
3)если f(x) и фи(х) непрер в т х=а прин Д(f) и Д(фи), то: тоже непр в т х=а; 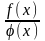непр, если 4)если f(x) непр в т х=а, а g(y) непрв т f(a), то сложная ф-циянепр в т х=а. Глобсв-ва: 1)(Больцано-Коши) Если f(x) непр на отр [a,b] и на концах отр принимает знач разных знаков, т.е. f(a)*f(b)<0, то сущ с прин [a,b] такое что f(c)=0; 2) (Вейерштрасса)если f(x) непр на [a,b], то она ограничена и на этом отрезке существуют точки , в которых функция f принимает свои найбольшее и найменьшее значения; 3) (кантора) если f(x) непр на отр [a,b], то она и равномерно непрерывна на нем.

Т(непрерюэлем.ф-ций) Каждая элементарная ф-циянепрер. во всех точках своей естественной области определения.