2. Кривые в трёхмерном евклидовом пространстве. Касательная, нормальная и соприкасающаяся плоскость кривой. Канонический репер кривой. Кривизна и кручение кривой.

Простейшими кривыми в пр-ве Е₃ наз. люб. прямая, отр, луч. Фигура γ₀⊂Е₃ наз. элем. кривой, если она гомеоморфна одной из прост. кривой. Фигура, гомеоморфная отр, наз. дугой. Кривой наз. фигура, кот. можно покрыть конечным или счетным множ. элем. кривых. Кривая γ₀ наз. гладкой кривой класса С^k, где к-некот нат. число, если ф-ции x(t), y(t), z(t) имеют в промежутке I непрерывные производные до порядка k включительно, причем в каждой т.tϵI должно вып: ранг ||x,y,z||=1. Простая кривая γ наз. гладкой класса С^k (k≥1), если у каждой ее внутр. т.М сущ. такая ε-окр B(M,ε), что пересечение γ∩B(M,ε) –гл. кривая класса С^k. Пусть ур-ния x=x(t), y=y(t), z=z(t) определяют кривую γ в некот. обл. U изменения перем t. Эта кривая наз. кусочно-гладкой, если обл. U можно покрыть не более как счетным множ. промежутков I_k, внутри каждого из кот. данные ур-ния определяют гл. кривую. Вектор N⃗=dτ⃗/ds наз. вектором кривизны кривой γ в т.М, а его длина |N⃗|=k-кривизной кривой γ в этой т. Т: для того чтобы кривая была прост, необход и дост, чтобы кривизна была=0 в кажд. точке этой кривой. dβ⃗/ds= –xv⃗. Число х наз. кручением кривой в т.М. Пусть γ:r=r(s) – гл. кривая, S – нат-ный параметр. Будем строить репер тесно связ-ный со св-ми данной кривой. Вектор τ⃗=dr/ds – един-й вектор касат-й в т.M. На всей кривой γ получим вектор-ф-цию τ=τ(s). Вектор N=dτ/ds наз. вектором кривизны γ в т.M. |N|=k наз. Кривизной кривой γ в т.M. На всей кривой γ k=k(s) явл. ф-цией парам-ра S. Итак, k=|N⃗|=|dτ/ds|=|d²r/ds²|.

Т. Гладкая линия γ явл. прямой или её частью ↔ k ≡ 0 ∀Mϵγ.

→) Пусть γ – прямая или ее часть. Тогда γ:r=r₀+ps, где p- един-ный направл-ный вект. прямой, S – нат. парам. Найдем k =|d²r/ds²|=|(d/ds)(dr/ds)|=|d⃗/ds|=0.

←) Пусть дана кривая γ:r=r(s) и ∀Mϵγ k=0. Тогда 0=|d²r⃗/ds²|=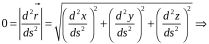 d²x/ds²=0,d²y/ds²=0, d²z/ds²=0. Решаем эту систему дифференциальных ур-ний: dx/ds=p₁, dy/ds=p₂, dz/ds=p₃, где p₁, p₂, p₃ - некоторые константы. Далее, x=p₁s+x₀, y=p₂s+y₀, z=p₃s+z₀, x₀,y₀,z₀ - некоторые константы, SϵI. Это параметрические ур-ния прямой или ее части. ŸДалее будем рассм-ть кривую γ, у кот. кривизна k≠0 ∀Mϵγ. Строим репер дальше. Прямая (M,N), Mϵγ наз. главной нормалью кривой в т.М. Вектор v⃗=N/k≡N/|N⃗| наз. единичным вектором главной нормали. Тогда N=kv или dτ/ds=kv⃗. Вектор β=[τ,v] наз. единичным вектором бинормали. Это наз-е оправдано тем, что β⊥τ,v и |β|=1 по опр-нию вект-го произвед. векторов.

Пр. (M,β), Mϵγ наз. бинормалью.

Итак, в производной т.М кривой γ мы получили правый ортонормир-й репер R_M=(M,τ,v,β), кот. наз. канонич-м репером в т.М или подвижным репером. Кординатные пл-ти этого репера называются: (M,τ,v) – соприкасающаяся пл-ть, (M,v,β) – нормальная пл-ть, (M,τ,β) – спрямляющая пл-ть. Найдем соотн-я между вект-ми подвиж. репера и их производными. Т.к. |v|=1. Тогда по лемме dv/ds⊥ →dv/ds f(M,τ⃗,β⃗)→ вектор dv/ds раскладывается только по векторам τ,β подвиж. репера: dv/ds=ατ⃗+æβ⃗. Найд. коэф-т α. Продифф-м тожд-во <τ,v>=0. Тогда <dτ/ds, v⃗>+<τ⃗ ,dv/ds>=0. Подст-м выраж-я для производных:<kv,v>+<τ,ατ+æβ>=0→k+α=0 (Здесь мы исп-ли, что |v|=|τ|=1, τ⊥β). Т.о., α=–k и dv/ds=–kτ⃗+æβ⃗. Ост. найти dβ/ds. Продиф-м тожд-во β=[τ,v]: dβ/ds=[dτ/ds,v⃗]+[τ⃗,dv/ds]=[kv⃗,v⃗]+[τ⃗,kτ⃗+æβ⃗]=0⃗+0⃗+æ[τ⃗,β⃗]=–æv⃗.

Получили три тож-ва dτ/ds=kv⃗, dv/ds=–kτ⃗+æβ⃗, dβ/ds=–æv⃗. Они наз. функциями Френе. Число æ, определ-ся в каждой т.М кривой, наз. кручением кривой в этой т. При изменении т. на кривой число æ изм-ся, получаем ф-цию æ=æ(s). Ф-лы для вычисления кривизны k и кручения æ для кр., зад. в нат. Параметризации γ:r=r(s): k =|d²r/ds²|, æ=1/k²(dr/ds,d²r/ds²,d³r/ds³).Ф-лы для вычисления кривизны и кручения кривой, зад. в произв. парам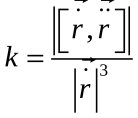-и: и , .

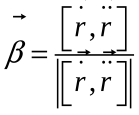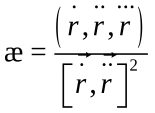Т. Пусть k=k(s), æ=æ(s) две гл. ф-ции, причем ф-ция k=k(s) неотриц. и ≠0. Тогда сущ. кривая, для кот. S будет длиной дуги, k(s) - кривизной, æ(s) - кручением.