2. Основные понятия и формулы комбинаторики.

Формула включения и исключения- это формула для подсчета числа элемента в объединении нескольких множеств.

Лемма1. (1)

Объединение двух множеств состоит из 3х областей: 1. часть принадлежащая только множеству А и не принадлежащая множеству В; 2. общая часть, т.е. принадлежит и А, и В; 3. Часть принадлежит только множеству В.

Тогда количество элементов по множестве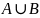 будет равно. Ч.т.д..

Аналогично можно получить утверждения объединения для 3х множеств.

Лемма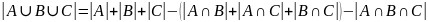2. (2)

Размещения с повторениями и без. Сочетания.

Пусть дано множество

Df. Набор элементов 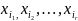из множества наз-ся выборкой объема r из nэлементов или (n, r) – выборкой.

Df. Если порядок следования элементов в выборке задан, то выборка наз-ся упорядоченной. Если же порядок следования элементов в выборке роли не играет, то такая выборка наз-ся неупорядоченной.

Замечание.Две упорядоченные (неупорядоченные) выборки с одними и теми же элементами, но разным порядком следования считается разными (одинаковыми).

Замечание. В выборках могут допускаться или не допускаться повторение элементов.

Df. Упорядоченная (n, r) – выборка, в которой повторение элементов допускается (не допускается) наз-ся (n, r)размещение с повторениями (без повторений).

Df. Неупорядоченная (n, r) – выборка, в которой повторение элементов допускается (не допускается) наз-ся (n, r)сочетание с повторением (без повторений).

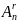Замечание. Введем след.обозначение: –число всех n, rразмещений с повторениями. – число всех n, r размещений без повторений. – число всех n, rсочетаний с повторением. – число всех n, rсочетаний без повторений. 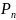– число всех перестановок.

Лемма1. .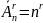

Замечание. Обозначим через 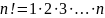, где .

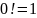Лемма2. .

Следствие. .

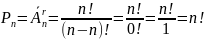Лемма3. .

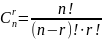Лемма4. .

Бином Ньютона.

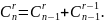Лемма1. . Лемма2. Лемма3. .

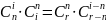Лемма4.(Бином Ньютона): (х+у .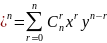

Следствие1. .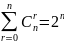

Следствие2. .

Следствие3. .

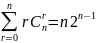Следствие4. .

Df. Числа наз-ся биноминальными коэффициентами.

2. Элементы логики высказ, математической логики и логики предикатов.

1. Высказывание – это мысленное отражение объективной связи между предметами. Оно истинно, если адекватно отражает эту связь, в противном случае – ложно. В естественном языке высказ. сущ. в виде повествов. предлож. Если это предлож. простое, т.е. описывает отдельный факт и не может быть разделено на более мелкие осмысленные предлож., то соотв. высказыв. наз. простым.

2. Роль союзов, с пом. кот. в естественном языке из простых предлож. формируются сложные, в формальном языке играют логические связки, называемые также логич. операциями.

3. Например, отрицание - ˥1=0, ˥0=1; конъюнкция - 1˄1=1, 0˄1=1, 1˄0=0, 0˄0=0; дизъюнкция - 1˅1=1, 1˅0=1, 0˅1=1, 0˅0=0; импликация - 1→1=1, 0→0=1, 0→1=1, 1→0=0; эквивалентность - А↔В=((А→В) ˄(В→А)).

4. Действие этих опер. (связок) можно предст. в виде символич. таблиц, кот. будем наз. таблицами истинности данных логич. операций. Напр., для операции отрицания таблица истинности выглядит так:

5. А	˥А
   1	0
   0	1

   Формула называется тождественно-истинной, или тавтологией (тожд.-ложной, или противоречием), если эта формула приним. знач. 1 (0) при всех наборах знач. переменных.

6. Основные законы логики: 1) закон тождества - «А есть А» или, для мат. логики: «а≡а». Доктор философских наук, проф. А. А. Ивин полагает: «Закон тождества выражает идею, что каждое высказыв. явл. необх. и достат. условием своей собственной истинности»; 2) закон непротиворечия – Два противопол. суждения не могут быть одновременно истинны касательно одного и того же предмета. Или, более частно, высказыв. и его отрицание не могут быть истинными одновр.: одно из них неизбежно ложно.

7. 3) закон исключения третьего - Из двух, отрицающих друг друга высказыв., одно истинно, другое ложно, а третьего (некоего промежуточного) не дано. 4) закон достаточного основания - Всякая истинная мысль должна быть достаточно обоснованной, в то время как, ложную, по настоящему обосновать невозможно.

8. Док-во от противного: Док-во утверждения А проводится след. образом. Сначала принимают предполож., что утвержд. А неверно, а затем доказыв., что при таком предполож. было бы верно некот. утвержд. В , кот. заведомо неверно. Полученное противоречие показыв., что исходное предполож. было неверным, и поэтому верно утвержд. ˥˥А, кот. по закону двойного отрицания равносильно утвержд. А.

9. Предика́т (n-местный, или n-арный) — это ф-я с мн-вом знач. {0,1}(или {ложь, истина}), определённая на мн-ве M=M₁xM₂x…xM_n. Таким образом, каждый набор элементов мн-ва M характеризуется либо как «истинный», либо как «ложный».

10. Предикат наз. тождественно-истинным и пишут: P(x₁,…,x_n)≡1,если на любом наборе аргументов он приним. знач. 1. Пред. наз. тожд.-ложным: P(x₁,…,x_n)≡0,если на любом наборе аргум. он прин. знач. 0.

11. Предикаты, так же, как высказыв., приним. два значения истинное и ложное, поэтому к ним применимы все операции логики высказыв.

12. Кванторы: Высказ. «для всех х» (для любого х, для каждого х) наз. квантором общности и обозн. ∀х. Высказ. «существует х» (для некот. х, хотя бы для одного х, найдется такое х) наз. квант. существов. и обозн. ∃х.

13. Высказыв. «сущ. одно и только одно х» (для единств. знач. х) наз. квантором единственности : ∃! х.

14. Отрицанием высказыв. с квантором общности (∀х) Р(х) явл. высказыв. (∃х) 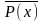, а отрицанием высказыв. с квантором существов. (∃х) Р(х) – высказыв. (∀х) . Для отрицания высказыв. с двумя переем.(∀х)( ∃ у) Р(х; у)использ. след. формула: (∃х)( ∀у)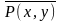 .