2. Параллельное проектирование и его свойства. Изображение плоских и пространственных фигур в параллельной проекции. Позиционные задачи.

Для изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием. Этот способ изображения состоит в следующем. Берем произвольную прямую , пересекающую плоскость чертежа , проводим через произвольную точку фигуры прямую, параллельную . Точка пересечения этой прямой с плоскостью чертежа будет изображением точки . Построив таким образом изображение каждой точки фигуры, получим изображение самой фигуры.

Свойства параллельного проектирования:      Свойство 1. Если прямая параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая. 

Свойство 2. Проекция отрезка при параллельном проектировании есть точка или отрезок, в зависимости от того лежит он на прямой, параллельной или совпадающей с прямой l, или нет. Параллельное проектирование сохраняет отношение длин отрезков, лежащих на прямой, не параллельной и не совпадающей с прямой l. В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка. 

Свойство 3. Если две параллельные прямые не параллельны прямой l, то их проекции в направлении l могут быть или параллельными прямыми или одной прямой.

Примеры изображений пространственных фигур на плоскости:  =Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами.

= При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами Аналогичным образом изображается прямоугольный параллелепипед.

 = Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий ее основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.   =Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий ее основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить ее с вершинами многоугольника. Полученные отрезки будут изображать боковые ребра пирамиды. 

=Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований.  =Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через нее две образующие, являющиеся касательными к этому эллипсу. 

2. Графы. Виды графов, способы их задания. Числовые характеристики графов.

ОПР: Графом G=(V,E) наз совокупность непустого множ-ва V и множ-ва Е, состоящего из пар эл-тов мн-ва V.

ЗАМ: В целях наглядности граф удобно изобр на пл-сти: каждому эл-ту мн-ва V ставят в соотв вершину, а каждому эл-ту мн-ва Е линию, соед-щую соответств-е вершины.

ОПР: Если в графе G=(V,E) во мн-ве Е пары явл неупоряд-ми, то эти пары наз ребрами, эл-ты мн-ва V – вершинами, а сам граф- неориентированным.

ОПР: Если в графе G=(V,E)во мн-ве Е пары явл упоряд-ми, то они наз дугами, эл-ты мн-ва V- вершинами, а сам граф – ориентированным или орграфом.

ОПР: Ребро вида (V_i , V_i) наз-ся петлей.

ОПР: Граф, имеющий петли, нз-ся псевдограф.

ОПР: Одинаковые пары мн-ва Е наз-ся кратными ребрами.

ОПР: Граф, имеющий, кратные ребра наз-ся мультиграфом.

ОПР: Граф, не имеющий петель и кратных ребер наз-ся простым.

Виды графов:

1. ОПР: Граф, в кот любые 2 верш соединены ребром наз полным графом.

2. Граф наз-ся регулярным в степени n, если степень каждой вершины этого графа равна n.

3. Граф G=(V,E) наз-ся двудольным, если мн-во его вершин V можно разбить на 2 подмн-ва V₁ и V₂так, что ребра соединяют вершины только лишь из разл подмножеств.

4. Граф наз-ся связным, если в нем любые 2 вершины соединены цепью, иначе граф наз-ся несвязным.

5. Граф наз-ся ориентированный, если он состоит упорядоченных пар вершин. Такой граф наз-ся также направленным графом или орграфом.

Графы могут задаваться след способами:

1. Задание графа G=(V,E) перечислением эл-тов мн-в V, E.

2. Задание графа графически (для этого на пл-ти каждому эл-ту мн-ва V будет соотв вершина, а каждому эл-ту мн-ва Е – линия, соед-щая соответствующие вершины).

3. Задание графа матрицей смежности А. (Для неориентированного графа эл-ты a_ij этой матрицы определяются след образом: ).

4. Задание графа матрицей инциденции: (Пусть дан граф G=(V,E), в котор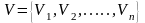ом: , , тогда эл-ты b_ij матрицы инциденции В опред-ся след. образом: )

ОПР: Цикл в графе G=(V,E) наз-ся Эйлеровым, если он содерж каждое ребро графа ровно 1 раз. (Граф наз-ся Эйлеровым, елси в нем имеется Эйлеров цикл).

Т: Связный граф G=(V,E) явл Эйлеровым ↔, когда степень каждой его вершины четная.

ОПР: Гамильтоновым путем (циклом) графа G называется путь (цикл), который проходит через каждую его вершину только один раз. (Граф, содержащий гамильтонов цикл, называется гамильтоновым.)