2. Трехмерное евклидово пространство. Векторное произведение векторов. П риложения к решению задач.

ОПР:Векторным произведением двух векторов называется вектор , обладающий следующими свойствами:

1) , где  - угол между векторами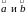   2)

3) векторы образуют правую тройку векторов.

Свойства векторного произведения:

1) (антикоммутативность); 2) ;

3) 4)  

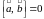
5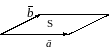 ) (геометрический смысл векторного произведения):

модуль векторного произведения 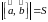- площади параллелограмма, построенного на векторах .

Теорема (о вычислении векторного произведения).

Пусть , . Тогда

Замечание. Для векторов на плоскости (с двумя координатами) векторное произведение не определено.

2. Взаимное расположение двух плоскостей, прямой и плоскости, двух прямых в трехмерном пространстве.

Пусть в некоторой аффинной системе координат даны пл-ти σ₁ и σ₂ своими ур-ями:

π_1: А₁x+B₁y+C₁z+D₁=0 (1) π_2: А₂x+B₂y+C₂z+D₂=0 (2)

Выясним взаимное расположение этих пл-тей. Т.к. координаты каждой общей точки пл-тей σ₁ и σ₂ явл. решением сис-мы ур-ий (1), (2) и обратно (т.е. каждое решение сис-мы ур-ий (1) и (2) явл. координатами общей точки пл-тей σ_1, σ₂ ), то вопрос о взаимном расположении 2-х пл-тей σ_1, σ₂ сводится к исследованию сис-мы линейных ур-ий (1) и (2). Обозн. Через r и r^’ соответственно ранги матриц:

А₁ B₁ C₁ и А₁ B₁ C₁ D₁, А₂ B₂ C₂ и А₂ B₂ C₂ D₂

Ясно, что r≤r^’, причём по теореме Кронекера-Капелли сис-ма ур-ий (1) и (2) совместна т. и т.т. к. r=r^’. Т. обр., пл-ти σ₁ и σ₂ имеют хотя бы одну общую точку тогда и только тогда, когда r=r^’. Возможны след. случаи:

1) r^’=1. Это означает, что коэффициенты А₁, B₁, C₁ и D₁ ур-ия (1) пропорциональны коэффициентам А₂, B₂, C₂ и D₂ ур-ия (2) (поэтому r=1) и ур-ия (1) и (2) равносильны. Отсюда заключаем, что каждая точка одной из пл-тей σ₁ и σ₂ принадлежит другой пл-ти, и поэтому пл-ти σ₁ и σ₂ совпадают. Это надо понимать так: 2-а ур-ия (1) и (2) определяют одну и ту же пл-ть. Обратно, если пл-ти σ₁ и σ₂ совпадают, то они имеют одно и то же направляющее подпр-во, поэтому по Т. векторы а (0, - C₁ ,В₁), b ( C₁ ,0, А₁), с (- B₁ ,А₁, 0) параллельны пл-ти σ₂, т.е.B₂ (-C₁ )+С₂B₁=0, А₂ (-C₁ )+С₂А₁=0, А₂ (-В₁ )+В₂А₁=0 (лемма о параллельности вектора и пл-ти). Т. обр., r=1, а т.к. сис-ма ур-ий (1) и (2) совместна, то r^’=1. Итак, пл-ти σ₁ и σ₂ совпадают тогда и только тогда, когда r^’=1.

2. r^’=2, r=2. Тогда пл-ти σ₁ и σ₂ различны ( они не могут совпасть, т.к. r^’>1) и имеют хотя бы одну общую точку, поэтому они пересекаются по прямой.

3. r^’=2, r=1. Сис-ма ур-ий (1) и (2) несовместна, поэтому пл-ти σ₁ и σ₂ не имеют общих точек, т.е. параллельны.

Рассм. теперь взаимное расположение 2-х прямых.

Пусть в пр-ве даны: прямая d₁ – точкой М₁ и направляющим вектором р₁ и прямая d₂ – точкой М₂ и направляющим вектором р₂. Оказывается, что по векторам М₁М₂, р₁, р₂ можно определить взаимное расположение данных прямых. Возможны 4-е случая: 1) прямые скрещиваются; 2) прямые пересекаются; 3) прямые параллельны; 4) прямые совпадают. Рассм. каждый из этих случаев отдельно. Заметим, что прямые d₁ , d₂ лежат в одной пл-ти тогда и только тогда, когда векторы М₁М₂, р₁, р₂ компланарны и , значит, имеет место равенство М₁М₂*р₁* р₂=0 .(3)

1. Как известно, две прямые наз. скрещивающимися, если они не лежат в одной пл-ти (т.е. не существует пл-ти, содержащей каждую из этих прямых). Следовательно, для того чтобы данные прямые d₁ и d₂, были скрещивающимися, необходимо и достаточно, чтобы для них имело место неравенство

М₁М₂*р₁* р2≠0 (4)

2)       Пусть прямые d₁и d₂ лежат в одной пл-ти, и, следовательно, для них выполняется условие (3). Эти прямые пересекаются т.и т.т.к. их направляющие векторы не коллинеарны. Итак, прямые d₁и d₂ пересекаются т.и т.т.к. М₁М₂*р₁* р₂=0 и векторы р₁ и р₂ не коллинеарны..

3)         Прямые d₁и d₂, лежащие в одной пл-ти, параллельны, если они не имеют общих точек. Это будет только в том случае, когда векторы р₁, р₂ коллинеарны, а векторы М₁М₂ и р₁ не коллинеарны. Итак, прямые d₁и d₂ параллельны т.и т.т.к. векторы р₁ и р₂ коллинеарны, но векторы р₁ и М₁М₂ не коллинеарны..

2. Ясно, что прямые d₁и d₂ совпадают тогда и только тогда, когда векторы , р₁, р₂ и М₁М₂ попарно коллинеарны.

Рассм. взаимное расположение прямой и пл-ти.

Пусть в пр-ве дана прямая d точкой М₀(x₀, y₀, z₀) и направляющим вектором р (р₁, р₂, р₃), а пл-ть σ – общим ур-ем

Ax+By+Cz+D=0 в аффинной сис-ме координат. Возможны след. случаи: 1) прямая и пл-ть пересекаются, т.е. имеют одну общую точку; 2) прямая параллельна пл-ти; 3) прямая лежит в пл-ти. Рассм. каждый случай в отдельности.

1) Прямая d пересекает пл-ть σ тогда и только тогда, когда направляющий вектор р прямой d не параллелен пл-ти σ, т.е. когда Aр₁+Вр₂+Ср₃≠0 (5)

Чтобы найти координаты точки пересечения прямой и пл-ти, надо решить сис-му, состоящую из ур-ий прямой и ур-ия пл-ти.

2. Прямая d параллельна пл-ти σ тогда и только тогда, когда вектор р параллелен пл-ти σ, и точка М₀ не лежит в этой пл-ти. Итак, соотношения :

Aр₁+Вр₂+Ср₃=0,

Ax₀+Вy₀+Сz₀+D≠0

Выражают необходимое и достаточное условие того, что прямая d параллельна пл-ти σ.

3. Аналогично, прямая d лежит в пл-ти σ тогда и только тогда, когда выполняются рав-ва:

Aр₁+Вр₂+Ср₃=0,

Ax₀+Вy₀+Сz₀+D=0.