2. Построение системы целых чисел. Операции на множестве целых чисел и их свойства. Система рациональных чисел.

Система целых чисел.

Опр. ситсемой целых чисел называется система Z, кот. имеет след. вид Z=<Z,+,×,0, N, особое слож., особ. умножение>, кот. удовл. аксиомам 3 групп

1-аксиома кольца

1. ¥a,bЄZ сущ.!целое с, такое что а+в=с 2.¥a,b,cЄZ a+(b+c)=(a+b)+c

3. ¥a,b,cЄZ a+b=b+a (сл.комм.) 4.Сущ. 0ЄZ, что ¥aЄZ а+0=0+а=0

5.  ¥aЄZ сущ. а´ЄZ,что а+а´= а´+а=0 (сущ.симм.эл.)

6. ¥a,bЄZ сущ. сЄZ, что а·b=с (бин.опер.умнож.) 7.¥a,b,c сущ. а·(b·с)= (а·b)·с (умн.ассоц.)

8. ¥a,b,cЄZ а·(b+с)= а·b+а·с (зак.дистр.)

2-аксиомы расшир.

1. Полукольцо нат.чис.- <N, особое слож., особ. умножение>, Nвкл.вZ 2.¥a,bЄN, a+b= aособ.+b 3.¥a,bЄN а·b= аособ.·b

3-аксиома миним.

Пусть мн-во М вкл. в Z сод. в себе мн-во Nвкл.в М и пусть элем. a,bЄМ, тогда a-bЄМ=>М=Z (акс.миним.)

Св-ва Z

1. Кольцо Z обл. всеми св-ми произв.кольца 2)Бин.опер. +,· связ. с. отн. порядка след обр.

Т1. ¥a,b,cЄZ из того, что а>b, или а=b, или а<b=>а+с>b+с, или а+с= b+с, или а+с<b+с (монот.слож.)

(¥a,b,cЄZ) с>0, а>b, или а=b, или а<b=> а·с>b·с, или а·с= b·с а·с<b·с ; (¥a,b,cЄZ) с<0, а>b, или а=b, или а<b=> а·с<b·с, или а·с= b·с а·с>b·с;

Т2.Кольцо Z обл. областью. целосн.;

Т3. К. Z явл. располож. кольц., т.е. ¥aЄZ имеет место либо а>0,либо а=0, либо а<0

¥a,b а>0, b>0 а+b>0,а·b>0

Т4. К. Z явл. архим. упор. кольцом, т.е. в к.Z справ. теор. Архимеда (¥a,bЄZ), b>0 сущ. nЄN, что n·b>а;

Т5. ¥aЄZ не сущ. bЄZ, что число а<b<а+1;

Т6. Произв. двух целых чисел равно 0 <=> когда хотя бы один из множ. равен 0

Система рацион-х чисел.

Постр. поля Q-рац-х чисел произв. с целью деления (кроме дел. на 0). Сист. Q=<Q,+,×,0, Z, особое слож., особ. умножение> наз. сис. рац. чисел если она удовл. след. аксиомам:

=¥a,bЄQ сущ.! сЄQ, такое что а+в=с =¥a,b,cЄQ a+(b+c)=(a+b)+c

=¥a,bЄQ a+b=b+a (сл.комм.) =Сущ. 0ЄQ, что ¥aЄQ а+0=0+а=0

=¥aЄQ сущ. а´ЄQ,что а+а´=0 (сущ.симм.эл.) =¥a,bЄQ сущ.! рЄQ, что а·b=р (бин.опер.умн.)

=¥a,b,cЄQ а·(b·с)= (а·b)·с (умн.ассоц.) =¥a,bЄQ а·b= b·а

=¥a,b,cЄQ а·(b+с)= а·b+а·с (зак.дистр.) =¥a,bЄQ а не равно 0=>сущ. хЄQ, что ах= b

Акс.расш.

<Z, особое слож., особ. умножение> Z ЄQ ¥a,bЄZ а+b=а особ.+b ¥a,bЄZ а·b=а особ.·b

Акс.миним. всяк.подмн М вкл. в Q совп. с Q, если выполн. след. услов.

1. Z содерж. В М 2)¥a,bЄМ из кот. а не равно 0, частное b/аЄМ

Из первых 10 аксиом след., что Q явл. полем

Св-во рац. чисел

Всякое рац.число есть частн.двух целых чисел (¥aЄQ) сущ. k,lЄZ, l не равно 0, что а=k/l

1.Z подкольцо кольца Q. 2. ур-е a*x=b, a#0 одноз-но разреш. ¥a,bЄQ. 3. Q должно быть миним. расш. с-ы Z. С-а Q явл-ся полем, кот. наз-ся поле рац-х чисел.

Св-ва мн-ва Q. 1. В Q нет ни наим, ни наиб. числа. 2. Q – счетное мн-во, т.к. можно устанть биек-е отображ-е, f:Q>--->>N. Q-полтно, т.е. что между ¥ 2 пац-ми числами нах=ся беск-но много рац-х чисел. 4.Q- поле рац-х чисел. 5. Поле Q явл-ся лин.-упор-м полем.

2. Плоскость Лобачевского. Аксиома Лобачевского. Аксиома Лобачевского и простейшие следствия из нее. Взаимное расположение прямых на плоскости Лобачевского.

ОПР:С-ма аксиом вкл. в себя: основные объекты, основные отнош, произв объекты, производные отношения, список аксиом. Затем получаются следствия из с-мы аксиом (с.а.).

ОПР:Осн объекты – объекты, кот только называются, но не определяются(прямая, точка).

ОПР:Производные объекты – объекты, которые определяются(окружность).

ОПР:Основные отношения – отношения, которые только называются, т.е. не дается определение (принадлежность, конгруэнтность).

ОПР:Производные отнош – отнош., для кот дается df (||-ность прямых, перп-сть прямых).

Следствия(теоремы):Аксиоматическое построение геометрии было еще в 3 веке. В с.а. Гильберта основными объектами были – точки, прямые, плоскости. Основные отношения – принадлежности, порядка, конгруэнтности. Аксиомы Гильберта разбиты на 5 групп. 1-я – аксиомы принадлежности, 2-я – аксиомы порядка, 3-я – аксиомы конгруэнтности, 4-я – аксиомы непрерывности, 5-я – аксиома параллельности.

1-я гр. А1: такая прямая а единственная (также обознач. АВ)

А2:

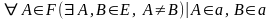
А3: существ. По крайней мере 3 точки, не лежащие на одной прямой. Если точки А, В, С не лежат на одной прямой, то пишут: .

2-я гр. Если точка В лежит между точками А и С, то мы запишем это так:

А1: 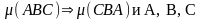-- три различные точки прямой

А2:

А3: Из трех различных точек прямой не более одной точки лежит между двумя другими.

3-я гр. А1: Если даны отрезок [АВ] и луч [OX), то

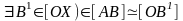
А2:

А3:

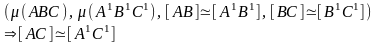
4-я гр. А1: (аксиома Архимеда)

А2: (аксиома Кантора) Пусть на какой-либо прямой а дана бесконечная посл-ть отрезков 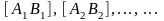удовлетворяющая двум условиям:

а) каждый последующий отрезок есть часть предыдущего

б) для любого наперед заданного отрезка [CD] найдется натуральное число 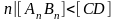тогда на прямой а сущ-ет точка М, принадлежащая каждому из отрезков этой посл-ти.

5-я гр. Пусть даны прямая а и точка 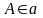. Тогда в плоскости (А,а) существует не более одной прямой, проходящей через точку А и не пересекающей прямой а.

Были попытки доказать 5-ю аксиому, т.е. вывести ее из остальных аксиом. В этом и заключалась проблема данной аксиомы: зависит или не зависит она от остальных аксиом. Пытались доказать методом от противного(через точку не принадлежащей на данной прямой можно провести более одной прямой не пересекающую заданную)

Требования к с.а.: д.б. непротиворечивой. С.а. – наз. непротиворечивой если из нее нельзя получить двух взаимоисключающих следствий.

Предположим, что основн. объектам аксиоматики дано конкретное истолкование в виде реальных объектов, а основным отношением тоже дано конкретное истолкование в виде реальных отношений с реальными объектами. Если для так введенных реальных объектов и реальных отношений выпол-ся все аксиомы данной с-мы, то говорят, что построена модель или интерпретация с-мы аксиом.

Пусть имеется 2 модели данной аксиоматики и что м/д одноименными основными объектами этих моделей существует биекция, при чем сохраняются все основные отношения. В этом случае говорят, что 2 модели изоморфны.

1)пересек. 2) || 3) расходящиеся

2. Трехмерное евклидово пространство. Скалярное произведение векторов. Приложения к решению задач. Евкли́дово простра́нство  — векторное пространство с заданным на нем скалярным произведением. В этом случае предполагается, что пространство имеет размерность равную 3 (трехмерное).

• ОПР:Скалярным произв 2-х вект 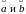наз число (1) (где  - угол м/ду ве-рами 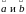 , отложенными из одной точки).  Из равенства (1) следует, что скалярное произведение в-ров a*b=0когда эти в-ры_|_.

Рассмотрим а*а (скал.пр-е) a*а=|a|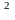 =a²- скалярный квадрат в-ра а. |a|=

Пусть в‑ры а и b заданы своими корд. в некотором ортонормированном базисе i, j, k: а(а₁,а₂,а₃)b(b₁,b₂,b₃).

Т1. Пусть , . Тогда . СЛ:  . ЗАМ: Для векторов на плоскости, соответственно, ; .

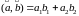Свойства cкалярного произведения:

1) для любых векторов , 2) для любых векторов и числа , 3) для любых векторов 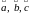, 4)

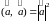
5) (при этом считается, что нул вектор перп любому), 6) .

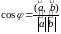ОПР:Ортонормированным репером в трехмерном пространстве называется совокупность начальной точки О и векторов 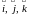, таких, что:

1) (единичные векторы),

2) (попарно перпендикулярные),

3) векторы образуют правую тройку векторов, то есть из конца вектора поворот от вектора 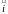к вектору 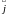виден в положительном направлении – против часовой стрелки.

ОПР: Коорд-ми вектора 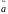наз-ся его проекции а₁, а₂, а₃ на оси коорд. Обозн: .

Угол между векторами: 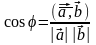.  т.е.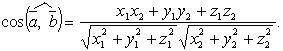     

Расстояние между точками: Есть две произвольные точки A1(x1;y1;z1) и A2(x2;y2;z2)  Тогда расст м/ду т A1 и A2 вычисляется: 

ОПР: Пусть дан отрезок АВ, тогда длина отрезка АВ называется длиной или модулем вектора: .