Отношение сравнения в кольце целых чисел.
Опр:
Целые числа
a и b наз сравнимыми по modm
если они принадлежат одному и тому же
классу вычетов по modm. Простейшие
св-ва сравнений:
1)a
сравнимо с самим собой по modm(рефлексивность);
2)если
,
то
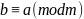(симметричность);
3)если
и
то
(транзитивность);
4)если
и
,
то
и
;
5)если
,
то то
;
6)к
любой части сравнения можно прибавить
и вычесть из неё число кратное по модулю;
7)если
то
,
то
;
8)если
,
то
;
9)если
и если
,
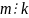то
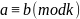где
;
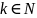10)если
и если d=ОД(a,b),
и если (d,m)=1
следоват.
где
.
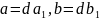Функцией
Эйлера φ(m)
наз-ся число по mod
m
взамно простых с m
или число нат-х чисел <m
и взаимно простых с m.
Т.Эйлера:
если
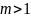и (a,m)=1,
то
.
Т.Ферма: если
p – простое число и (a,p)=1,
то
.
Т.Вильсона:
если p – простое число, то
.
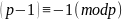Любое сравнение
1-ой степени
с одной переменной можем привести к
виду
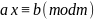где a
не сравнимо с нулём по modm.(*) Т.:1)если
в сравнении (*) (a,m)=1,
то сравнение (*) имеет единственное
решение; 2)если
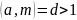и
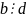следоват.
сравнение не имеет решений; 3)
если
и
следоват.
сравнение имеет d-решений, первое
решение
.
Сравнения
по простому модулю. Пусть
p – простое число, рассмотрим теоремы,
относящиеся к сравнению вида:
.
(1). Т1.:
сравнение вида (1) равносильно сравнению
степени не выше p-1. Д-во:
деля f(x)
на
,
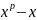имеем f(x)=(
)Q(x)+R(x),
где степень R(x)
не выше p-1. А т.к.
,
откуда и следует теорема. ч.т.д.
Т2.: если
сравнение (1) имеет более чем n решений,
то все коэффициенты f(x)
кратны p. Простейшая система сравнений
относительно попарно взаимно простых
модулей
,
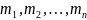
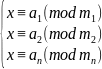всегда разрешима, и её решение единственно
по модулю
.
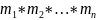Периодической
дробью наз-ся
бесконечная десятичная дробь, в которой,
начиная с некоторого места, стоит только
периодически повторяющаяся определённая
группа цифр. Например, 1,3181818...; короче
эту дробь записывают так: 1,3(18), (и говорят:
«18 в периоде»). П.
д. называется
чистой,
если период начинается сразу после
запятой, например 2(71) = 2,7171..., и смешанной,
если после запятой имеются цифры,
предшествующие периоду, например
1,3(18). С помощью теории сравнений можно
решать различные математические задачи.
К основным арифметическим
приложениям теории сравнений относятся
– нахождение длины периода десятичной
дроби и признаки делимости.
Аксиоматические теории и схема их построения. Построение системы натуральных чисел.
Математику можно обосновать только аксиоматическим методом. Аксиом.сист. вкл. в себя: первичные терм., аксиомы, теоремы. Аксиом. теория дел-ся на 2 группы:1.содержательные 2. формальные
Опр. Если при описании теории сист. логических правил вывода предпол. известн., то теория наз. содерж.
Опр. Если использ. сист. логич.правил выводов вкл.в теорию, то такая теория наз.формальной.. Форм.теория – мн-во формул некот. алфавита вместе с мн-вом правил вывода в том же алфавите и с некот. выделенным подмн. формул из этого мн-ва (сист. акс.)
Замеч.. Все известные нам теории за искл. логики высказываний явл. содерж.
Опр. Если есть высказывание А и не А и не более чем одно из них не истина, то теория явл. непротиворечивой.
В большинстве случаев непрот. доказывается косвенно (непрот. одной теор. относ. другой) связана с тем, что в одной теории не могут сущ. 2 утв. А и не А. Данная теор. непрот., если для нее удал. найти модель из объектов другой заведомо непротив. теории.
Опр. теор. Т1 назыв. интерпр. теор. Т если каждому истинному утв. в теор. Т соотв. истинное утв. В теор. Т1. Опр. интерпр. Т1 аксиом. теории Т наз. моделью т. Т если каждой аксиоме из Т соотв. истинное высказ. теор. в Т1.
Система натуральных чисел.
Аксиомы Пеано: 1) В N cущ. ! элем. a’ непосредст. следующий за а. 2) Для люб-го числа а из N сущ-т ! эл-т а’ непосредственно следующий за а. 3) Для люб. элем-та из N сущ. не более 1 эл-та за которым непосредственно следует данный эл-т. 4) Пусть М ċ N и выполн-ся: 1. 1€ М 2. если а€М след-но а’€M тогда М=N
опр: Любое множество N для эл-тов кот. установлено отношение ‘непосредственно следовать за’ удавлет-щее аксиомама Пиано наз-ся множеством натуральных чисел.
Алгебр-ие операц-и на N: 1. Сложение – это алг. опер-я определенная на N и обладающая свойствами: 1.(для люб. а) а+1=а’ 2. (для люб. а,b) a+b’= (a+b)’ (a+b-сумма, а,b -слогаемые) Т.Сложение нат. чисел сущ и !. 2. Умножение: 1. для люб а а*1=а 2. для люб а,b a*b’=ab+a T/ Умножение нат чисел сущ. и !.
Свойства сложения: 1. для люб. а,bˆN a+b=b+a (комут-ть) 2. Длб люб. a,b,cˆN (a+b)+c=a+(b+c) (ассац-ть)
Свойства умнож-я: 1.(Для люб. а,bˆN) ab=ba 2. (для люб. a,b,c ˆN) (ab)c=a(bc) 3.(a,b,cˆN) a(b+c)=ab+ac
Операции вычитания и деления лишь частично выполняются на N. Отношение порядка на N: На N введем отношение ‘<’ cледующим образом: a<b (сущ. kˆN) (a+k=b) a,bˆN