Многочлены от одной переменной над полем. Производная многочленов. Нод двух многочленов и алгоритм Евклида. Неприводимые многочлены.
ОПР:Многочленом от переменной x над полем P называется выражение вида a0+a1x+...+anxn,
где n-любое целое неотрицательное число,ai
P(i=
).
Т.к.мы рассматриваем многочлен над полем, то всякий многочлен f(x) P[x] делится на любоймногочленa0 P[x]нулевой степени.
Опр.Пустьf1(x),...,fk(x) ‑многочленыизP[x].Многочлен d(x) принадл P[x]наз.общим делителемэтих многочленов,если все они делятся на d(x).
Т.к. всякий многочлен из P[x] делится на любой отличный от 0 элемент поля P, то среди общих делителей fi(x)(i=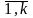
) всегда будут многочлены нулевой степени.
Опр.Наибольшимобщимделителем(НОД)неравных0одновременномногочленовfi(x) P[x],i= ,наз.такойихобщиеделитель(сокр.ОД)D(x),которыйделитсяналюбойОДэтихмногочленов.
ДлянахожденияНОДдвухмногочленовf(x)и
(x)
0наполеPслужиталгоритмЕвклида.
Алгоритм Евклида позволяет найти наибольший общий делитель двух многочленов, т.е. многочлен наибольшей степени, на который делятся без остатка оба данных многочлена. Алгоритм состоит из последовательного деления с остатком сначала первого данного многочлена, f(x), на второй, g(x): f(x) = g(x)∙q1(x) + r1(x), (1)
затем, если r1(x) ≠ 0, – второго данного многочлена, g(x), на первый остаток – на многочлен r1(x): g(x) = r1(x)∙q2(x) + r2(x), (2)
далее, если r2(x) ≠ 0, – 1го остатка, r1(x), на второй остаток, r2(x): r1(x) = r2(x)∙q3(x) + r3(x), (3)
затем, если r3(x) ≠ 0, – второго остатка на третий: r2(x) = r3(x)∙q4(x) + r4(x), (4)
и т.д. Поскольку на каждом этапе степень очередного остатка уменьшается, процесс не может продолжаться бесконечно, так что на некотором этапе мы обязательно придем к ситуации, когда очередной, n + 1-й остаток rn + 1 равен нулю:
rn–2(x) = rn–1(x)∙ qn(x) + rn(x), |
(n) |
rn–1(x) = rn(x)∙ qn+1(x) + rn+1(x), |
(n+1) |
rn+1(x) = 0. |
(n+2) |
Тогда последний не равный нулю остаток rn и будет наибольшим общим делителем исходной пары многочленов f(x) и g(x).
Теорема:НОДдвухмногочленовравенпоследнемуненулевомуостаткувалгоритмеЕвклидадляэтихмногочленов.
Опр.Многочленf(x) принадл P[x]положительнойстепениназ.неприводимымнадполемР,еслиегонельзяразложитьвпроизведениемногочленовстепени<n,но>0.
Опр.Многочленf(x) принадл P[x]положительной степени наз.приводимым над полем Р,если
если он не является неприводимым.
ТеоремаВсякий многочленf(x) принадлP[x]положительной степени м.б.разложен в произведение неприводимых над полем Р многочленов, и это разложение единственно с точностью до
порядка следования множителей и множителей нулевой степени,т.е.разложение многочлена
f(x) на неприводимые множители м.отличаться лишь порядком записи множителей, а также
множителями нулевой степени.
Многочлены над полями с, r и q. Многочлены от n переменных. Алгебраические и трансцендентные числа.
ОПР:Всякое минимальное расширение поля R действительных чисел, содержащее элемент i,квадрат которого равен -1 наз. полем комплексных чисел(ПКЧ).
Осн теор алгебры. Всякий многочлен f(x) над ПКЧ имеет по меньшей мере один корень.
Или Всякий многочлен f(x) степени n 1в ПКЧ имеет ровно n корней.
ОПР:Поле Р наз. алгебраически замкнутым, если любой многочлен из кольца Р[x] имеет
столько корней какова степень этого многочлена.
Сл1. Всякий многочлен f(x) принадл С[x] степени n имеет n комплексных корней.
Учитывая опр.и сл1: ПКЧ алгебраически замкнуто.
ОПР:Неприводимыми над полем действительных чисел явл. многочлены первой степени
(когда корень действительный) и квадратные трехчлены с отрицательным дискриминантом.
Лемма: Если мн-н f(x) принадл Z[x] приводим в кольце Q[x], то он привод и в кольце Z[x].
Т:(Эйзенштейна)Если все коэффициенты многочлена f(x)= anxn+an-1xn-1+...+a1x+a0, кроме старшего, делятся на некоторое простое число р, и а0 делясь на р не делится на р2, то многочлен f(x) нерпиводим в кольце Q[x].
ОПР:Число альфа называется алгебраическим, если оно является корнем некоторого многочлена с целыми коэффициентами anxn+an-1xn-1+...+a1x+a0 (т.е.корнем уравнения
anxn+an-1xn-1+...+a1x+a0=0, где an,an-1,...,a1,a0---целые числа, n
1, an
0).
ОПР:Трансцендентное число‑число (действительное или мнимое), неудовлетворяющее
Никакому алгебраическому уравнению с целыми коэффициентами. Таким образом,Т.Ч.
противопоставляются алгебраическим числам
ОПР:Многочлен–это сумма одночленов, снабженных числовыми коэффициентами.
ОПР:Степенью многочлена называется наибольшая степень одночлена, входящего в этот
многочлен( с ненулевым коэффициентом).
ОПР:Многочлен называется однородным, если все его одночл имеют одну и ту же степень.
ОПР:Симметрический многочлен‑многочлен от n переменных F(x1, x2,…,xn) не изменя‑
ющийся при всех перестановках входящих в него переменных.
Т:Основная теорема теории симметрических многочленов гласит, что любой симметрическиймногочлен может быть представлен единственным образом в виде многочлена от основных
Симметрических многочленов.
Основная идея метода Штурма. Измененять две переменные (из-за этого метод Штурма упрощает многие неравенства из нескольких переменных) так, чтобы из одной части неравенства получилась другая и вдобавок к этому всегда изменяемая часть изменялась в одну, нужную нам, сторону (или увеличивалась, или уменьшалась). Обычно этого удается достичь изменяя два числа с постоянной суммой или произведением. Одним из способов решения уравнений 3-ей степени является метод Кардано: Формула Кардано — формула для нахождения корней канонической формы кубического уравнения
.
По формуле Кардано, корни кубического
уравнения в канонической форме
равны: 
где 
Недостаток формул Кардано остоит в том, что с их помощью рациональные корни часто представляются в виде иррациональных.
Одним из способов решения уравнений 4-ой степени явл метод Феррари, он состоит из двух этапов На первом этапе уравнения вида a0x4 + a1x3 + a2x2 + a3x + a4 = 0,приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.