2. Кольцо. Примеры колец. Простейшие свойства кольца. Подкольцо. Гомоморфизмы и изоморфизмы колец.

Опр. Кольцом называется непустое множество К, в котором определены две бинарные алгебр. операции - сложение и умножение, удовлетворяющие следующим аксиомам: 1) К - аддитивная абелева группа;2) умножение в К ассоциативно;3) умножение и сложение связаны дистрибутивными законами ("a,b,cÎK) a(b+c)=ab+ac; φ(a+b)=φ(a)+φ(b).

Если операция умножения в К коммутативна, то кольцо К называют коммутативным. Примерами коммутативных колец являются: множества: Z, Q, R, C, множество всех чисел вида a+bÖ2 где a,bÎQ, кольцо Z_m. Некоммутативными кольцами являются: кольцо Q_n*n квадратных матриц n-го порядка с рациональными элементами;

Свойства: 1) кольцо – аддитивная абелева группа (<*><+>)

2) $ единственный 0(нейтральный по +), "aÎK $!(-a)ÎK ; 3) 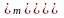; 4) <*> – на K дистрибутивно слева и справа. 5) "aÎK a*0=0ÎK; 6) "a,bÎK a*(–b)=(–a)*b=–(ab); 7) Пусть a¹0, если ab=acÞb=c; 8) K* множеств всех обратимых элементов кольца K с e образуют группу по <*>, которая называется мультипликативной группой кольца. Опр. подкольцом кольца К наз. непустое подмн-во кольца К, кот. само явл. Кольцом отн-но тех же операций. Т(крит.подкольца). Непустое подмножество К' кольца К отн-но операций сложения и умножения явл.подкольцом этого кольца тогда и только тогда, когда: 1) "a,bÎK’, a-bÎK’; 2) "a,bÎK’, abÎK’. Опр.Отображение f кольца К в кольцо К' называется гомоморфным (или гомоморфизмом), если для любых "a,bÎK f(a+b)=f(a)+f(b); f(ab)=f(a)f(b). Ясно, что понятие гомоморфизма колец является обобщением понятия изоморфизма: если f - биективное и гомоморфное отображение K на К', то оно изоморфно. Т. Гомоморфный образ кольца есть кольцо.

Док-во: Пусть f: <K,+,*>®<K₁,Å,Ä> f(K)Ì K₁ . Если К – кольцо, то f(K)– тоже кольцо. Ранее док-лось, что гомоморфный образ группы есть группа, т.е. f(K)– абелева группа по <+>. Покажем что на множестве f(K) определено умножение: f(K)={f(a)|aÎK} "f(a),f(b)Îf(K) a,bÎK f(a)Äf(b)=f(a*b) [гомом. – это f(aT₁b)=f(a)T₂f(b);]. Т.к. a,bÎKÞa*bÎKÞf(ab)Îf(K) "f(a),f(b) f(a)Äf(b)ÎKÞ на множестве f(K) определено умножение. Для того, что бы доказать что f(K)– кольцо, нужно док-ть, что умножение ассоциативно и дистрибутивно. 1) "f(a),f(b),f(c)Îf(K) (f(a)Äf(b))Äf(c)=f(ab)Äf(c)= f((ab)c)= ["a,b,c,ÎK, а в К ассоциативный закон выполняется] Þ=f(a(bc))=f(a)Äf(bc)=f(a)Ä(f(b)Äf(c). 2) аналогично док-жем что выполняется дистрибутивный закон: "f(a),f(b),f(c)Îf(K) (f(a)Åf(b))Äf(c) = f(a+b)Äf(c) = f((a+b)c) = f(ac+bc)= f(ac)Åf(bc) = f(a)Äf(c)Åf(b)Äf(c). 3) "f(a),f(b),f(c)Îf(K) f(c)Ä(f(a)Åf(b)) = f(c)Äf(a)Åf(c)Äf(b). f(K)– кольцо. Ч.т.д.

Теорема верна, когда f– изоморфизм.

Т.(о гомоморф.колец): пусть f – эпиморфизм кольца К на кольцо К₁ с ядром I. Тогда фоктор-кольцо изоморфно К₁.

2. Поле. Простейшие свойства поля. Поле q. Поле с.

Поле — множество F с двумя бин операциями   (аддитивная операция, или сложение) и  (мультипликативная операция, или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей  , все ненулевые элементы которого обратимы. Прмеры(Q — рац числа,R — вещ числа,C — комплчисла,)

Свойства:

1.образует аддитивную абелеву группу. 2.множении ассоциативно 3.умнож дистриб слева и справа относит сложения. 4.в поле нет делителей 0 5.в поле однознач разрешимо ур-е ax=b , 6.в поле опред опер деления.(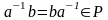 -остат от деления b на a.

Поле комплекс чисел.

Для реш. матем. з-ч действит чисел недостаточно. Одной из трудностей задач является нахождение корней уравнения . Построим поле, в кот имеет реш: рассм мн. 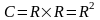, т.е. 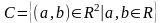и введём на этом множестве 2-е операции <+><*>

(a,b)+(c,d)=(a+c,b+d) (a,b)*(c,d)=(ac-bd,ad+bc)

Т. Мн-во С всех пар действит чисел с операциями <+><*> является полем. В С сущ эл-т 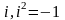–это пара(0,1).Т.ПолеС всех пардействчис,явл-сярасшполяRи содерж эл-т – наз полем компл чис.

ОПР:Запись комплексного числа   в виде x+iy, где   и y принадл R, наз-ся алгебраической формой комплексного числа.

ОПР:Если вещественную x и мнимую y части комплексного числа выразить через модуль r=|z|  и аргумент φ (x=r cos φ, y=r sin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме z=r(cos φ+i sin φ).

Действия над комплексными числами, записанными в алгебраической форме:

1. Сумма (разность) комплексных чисел: z₁ ± z₂ = (a₁ ± a₂) + (b₁±b₂)∙i,

2. Произведение комплексных чисел: z₁∙z₂ = (a₁∙a₂ - b₁∙b₂) + (a₁∙b₂ + a₂∙b₁)∙i,

3. Деление двух комплексных чисел осуществляется по следующему правилу: 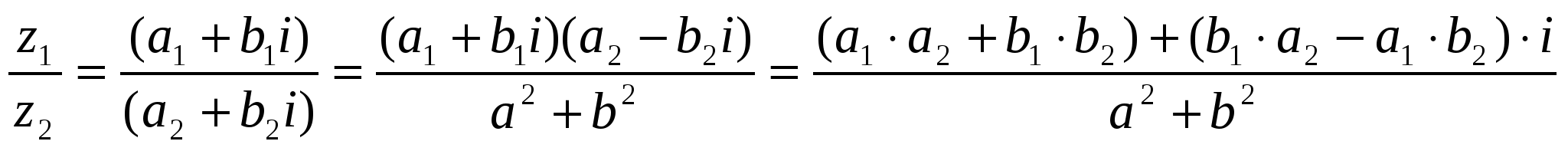, (z₂ ≠ 0),

4. Возведение в степень комплексных чисел: zⁿ=z*z*z (n раз). (применимы все свойства степеней).

Действия над комплексными числами, заданными в тригонометрической форме:

1. Умножение.При перемножении чисел z₁ и z₂, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:z = z₁z₂ = r₁r₂( cos( ₁ + ₂ )  isin( ₁ + ₂ )).

2. Деление.Если z₁ = r₁( cos₁ + isin₁) и z₂ = r₂( cos₂ + isin₂ ), то 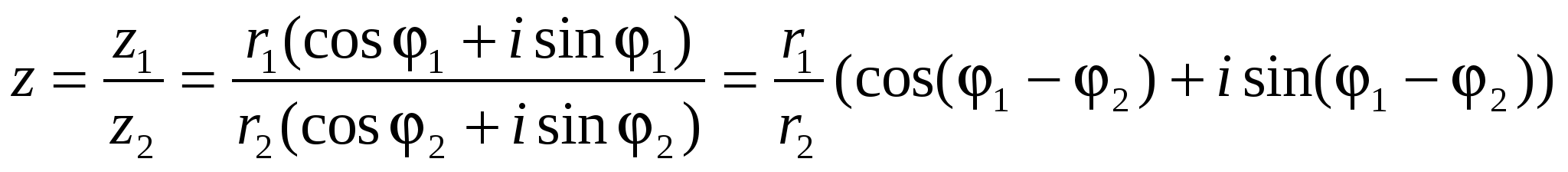, т.е. модуль частного двух комплексных чисел z₁ и z₂ равен частному модулей, а аргумент частного – разности аргументов.

3. Извлечение корня из компл числа.Корнем n-ой степени, n  N, n  2, из числа  z называется любое комплексное число u, для которого n-ая степень равна z: .