2. Дифференцируемость функции комплексной переменной (фкп).

Пусть 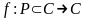, - однозначная, z₀-пред т.Р. Придатим т. z₀-приращение Δz≠0, так, чтобы приращ точки (z₀+ Δz )ЄР. Функция f получит приращение Δf(z₀)=f(z₀+Δz)-f(z₀).

ОПР: Если сущ конечный предел отнош приращ , то он наз производной функции в т. z₀.

ОПР: Ф-ция f(z) наз диф-мой в т. z₀ если её приращение в этой точке можно представить в виде (1).

Т: (крит. Дифф-ти ФКП): Ф-ция w=f(z) дифф-ма в т. z₀↔сущ f ‘ (z₀).

ОПР: Дифференциалом ф-ции f(z) в т z₀ наз главная линейная отн-но Δz часть приращения ф-ции, обозн df(z₀)=f “(z₀) Δz =f ‘(z₀)dz, dz= Δz.

Замеч: Т.к. понятие произв ФКП вводится также как и понятие действ переем, то ост в силе все осн правила дифференцирования.

Т: (необх условия диф-ти функции): Если ф-ция w=f(z)диф-ма в т z₀, то она непрерывна в этой точке.

_{Т( необх и дост усл диф-ти ВКП во внутр т обл определ} Коши-Римана): Пусть ф-ция f определена на мн-ве Р и сод-ся в С ( ),w=f(z)=u(x,y)+v(x,y) т. z₀ – внутр. точка, z₀=x₀+iy₀. Ф-ция f(z) диф-ма в т. z₀ ↔u(x,y) и v(x,y) дифф в т. как ф-ции двух переем в т. (х₀, у₀) имеет место усл Коши-Римана: , причем если f(z) дифф-ма в т z₀, то её произв в т. z₀ равна f '(z₀)=

2. Интеграл от функции комплексной переменной.

Пусть в пл-сти задана кривая L: x=x(t), y=y(t), tЄ[α,β]. Кривая L на компл пл-сти задается уравнением: z=z(t)=x(t)+iy(t), t [α,β].

ОПР: Если сущ конечный предел 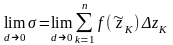, кот не зависит ни от разбиения кривой, ни от выбора точек, то он наз интегралом вдоль кривой L от функции f(z) и обозн: .

Т: Если ф-ция w=f(z) явл однозначно аналитической в односвязной обл G, γ-кусочно-гладкая замкнутая кривая , содержащаяся в G, то .

Т(о состовном контуре): Если ф-ция f(z) явл однозначной аналитической в многосв гран G и на её границе L состоит из замкнутых контуров γ₁, γ₂, γ_n, то .

Т(инт формула Коши): Пусть ф-ция w=f(z) явл однозначно аналит в G, L – кусочно-гладкая кривая, содержащаяся в G вместе со своей внутр обл Д, для любого эпселент >0 из Д имеет место формула: .

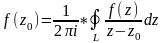Т(о разложении аналитической ф-ции в сх.степенной ряд): Пусть ф-ция f(z) явл-ся однозначной, аналитической в обл. G, r – расстояние от т-ки z0 до границы обл., тогда в круге Кr: |z-z0|< r ф-ция f(z) разлогается в сх. степ. ряд, т.е. для z Кr, f(z)=

2. Группы. Примеры групп. Простейшие свойства группы. Подгруппы. Гомоморфизмы и изоморфизмы групп.

ОПР: Непустое мн-во G эл-тов произв природы с опред на нем бин опер Т наз группой отн бин оп Т, если выполн след усл: 1)Операция Т на мн-ве G ассоциативна, 2) в G сущ хотя бы 1 правый неутральный эл-т отн Т, 3) в G , дл ялюбого эл-та сущ правый симметр эл-т.

ОПР: Подмн-во Н группы G наз подгруппой группы G , если Н явл группой отн групповой операции G. Обозн H<G.

Т.(критерийподгруппы)ПодмножНгруппыGотносбиноперTявлподгрупгрGт.ит.т.,когда:

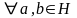
1. 2.

Док-во:(необх)Если H подгр,то1-2 вып-ся по Df. (достат) пустьвып усл1-2,тогдаН-гр.На мн-ве H опред опер Т согл усл1,Т-ассоц, т.к.Н-подмн-воG .Покаж, что в Н сущ нейтр:

Опр. Бин алгебраич операция   на множестве   наз коммутативной если   для всех  .

Опр. Бинарная алгебраическая операция   на множестве   называется ассоциативной, если   для всех  .

Пр. Операция слож   на мн-ве целых чисел   является коммутативной и ассоциативной.

ОПР: Группа по сложению всех элементов поля называется аддитивной, а группа по умножению всех его элементов, отличных от нуля, - мультипликативной группой поля.

Простейшие свойства группы:

1. Для любого элемента группы правый обратный элемент явл и левым обратным.

2. Для каждого элемента группы эл-т а^-1 явл единственным обратным эл-том.

3. Для любого эл-та группы правая единица явл также и левой еденицей.

4. Элемент е группы является единственным единичным эл-том группы. Также он явл единственным левым и единственным правым единичным эл-том группы.

5. Для любых эл-тов а, б группы каждое из уравнений ах=б, уа=б относительно переменных х и у имеет в группе единственное решение.

6. Для любых эл-тов а,б, с группы из ас=бс следует а=б и из СА=сб следует а=б.

7. В группе элемент а есть обратный к а^-1, т.е. (а^-1)^-1=а.

ОПР: Гомоморфизмом группы G в (на) группу Н называется отображение множества G в (на) Н, сохраняющее главные операции группы G.

ОПР: Гомоморфизм h группы G на группу Н называется изоморфизмом, если h является инъективным отображением множества G на Н.

ОПР: Пусть G и G’ — произвольные группы. Отображение 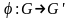  группы G в группу G’ наз гомоморфизмом (или гомоморфным отображением), если для любых эл-тов g₁, g₂  группы G имеет место рав-во