Множества, измеримые по Лебегу на прямой. Их свойства.
µ: H→[0;+∞]- мера.
Опр.
Пусть H полукольцо подмножеств множества
X, неотрецат. функция µ определённая на
H и принимаемая знач. от 0 до +∞ назю
мерой, если: 1) µØ=0; 2) A, Ak
H и A=
,
тогда µА=
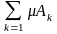
Опр.
µ→[0;+∞]. Неотриц. ф-ия µ заданная на
полукольце наз. объёмом, если выполняются
условия: 1)µ(Ø)=0; 2) для любого А
H,
дла люб. Аj
H,
A=
следовательно,
µА=
(аддитивность объёма).
Теор.
(продолж. меры с полукольца на кольцо):Пусть
µ мера задана на полукольце Ρ, тогда
сущ. единственная
:
k(P)→[0;∞], кот явл. мерой, а во вторых для
люб. A
P
(A)=µ(A),
где
–продолжение
меры.
Теорема(единственность
продолжения):Пусть
K – кольцо подмнох. множ. X. µ: K→[0;∞]– σ
конечная мера на K. Тогда любое продолжение
меры
:
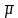σK(x) (на минимальное кольцо порождаемое
σ- кольцом K), единственна и σ- конечна.
Опр.
Пусть X– некоторое множество, K – кольцо
подмножеств, µ: K→[0;∞]. Мера µ наз.
конечной, если каждое множ. из K имеет
конечн. меру, т.е. для любого А
K
(µA<+∞). Мера µ наз. σ-конечной, если x
можно предстасить в виде: X=
,
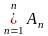
An
K
и µAn<+∞.
Опр.
(изм. множ. по Лебегу): σ-
алгебра
1
наз. измер. множеств по Лебегу на R. Множ.
A
1
наз. измер по Лебегу, µ=µ*/
1
– мера Лебега. (µ:
1→[0;∞]).
Свойства меры по Лебегу.
1.µ
– полная мера.(т.е.
подмн. множ. меры ноль измеримо по Лебегу
и имеет меру ноль).
2.Каждое одноточечное множество измеримо по Лебегу и имеет меру ноль.
3.Каждое счётное множество измеримо по Лебегу и имеет меру ноль.
4.
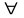
интервал
[a, b] измерим. µ[a, b]= b-a.
5. Каждый бесконечный промежуток измерим.
6.Каждое открытое множ. на числовой прямой измеримо, это след. из того, что открыт. множ. на числов. прямой представляет собой дизъюнктивное объед. не более чем счётного числа интервалов (огран., неогран.).
7.Мера открытого множ = сумме мер интервалов из кот. оно состоит.
8.Каждое замкнутое множ. на числовой прямой измеримо, т.к. замкнутое множ. . Множ. наз. замкнутым, если его дополнение открыто.
Опр.
Нижнняя грань, зависящая только от мн-ва
E наз. внеш мерой мн-ва E и обознач. m*(E)
(или μ*(E)). Из Опр. следует m*(E)
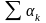m*E+ ε
Опр. Внутренней мерой мн-ва E наз. разность м/у длиной S отрезка и внешней мерой дополнительного мн-ва к E. (m*(E)=1- m*(СE))
Т.к
для того, чтобы мн-во E было измеримо
н. и дост. чтобы
ε>0 мн-во E м. представ в виде E= ε+e1-e2, где
ε–сис конеч числа попарно непересек-ся
интервалов, а мн-ва е1,е2 – мн-ва, у которых
вешняя мера
ε.
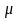(е1)
ε,
(е2)
ε.
При соблюдении этого условия справедливо:
m(ε)-ε
m(ε)
m(ε)+
ε.
Сравнение интеграла Римана с интегралом Лебега.
ОПР.
Если сущ. предел интегральной суммы
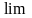
при
,
где 
=max{∆
xi}
стрем к беск,0≤k≤n-1
и этот предел не зависит не от выбора
точек ξ k не от способа разбиения 
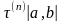отрезка [a,b] на конеч. Число частичн.
отрезков. Тогда этот предел наз. опред.
интегр. или инт. Рим ф-ии f отр.[a,b] и обозн.
Lim
=
при 
Опр.
Пусть f: E→
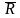явл. нейтральной ступенчатой ф-ей,
принимающей значения y1, y2,…,yn. yk≠yj, k≠j
и через множ. Ek={x
E│
f(x)= yk }– измер. множ.(k от 1 до n), тогда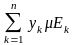
наз. интегралом Лебега от ф-ии f по мере
µ и обозначается (т.е.
).
Т
(σ-аддитивность интегр. Лебега):Пусть
f
L(x,µ)
(инт. по Лебегу на множестве Ч по мере
µ).
A
α,
(A):=,
:=0.
Тогда функция φ
явл.
σ-аддитивной функ. множеств. т.е. A=
.
Т (Лебега): Для того, чтобы ограниченная ф-ция f(x) была интегрируема по Риману необходимо и достаточно, чтобы она была непрерывна почти везде.
Т (необходимое условие интегрируемости) :Всякая ф-ция f(x) интегрируема по Риману, тог она интегрируема и по Лебегу, и оба её интеграла равны.
Т
(о восстановлении первообразных ф-ций)
Пусть ф-ция f(x) в каждой т-ке из [a,b] имеет
производную f’(x), тогда если f’(x) –
ограничена (k
x[a,b],
| f’(x)|k),
то f(x) интегрируема по Лебегу и справедлива
ф-ла f(x)= f(а)+
.
Простейшие свойства инт. Лебега:
1)Пусть
E – измеримое множество (E
α)
µE=0 и f заданное на множ Е– измеримоя
функция, тогда
=0.
2)
Пусть E – измеримо (E
α)
и f(x)=c (константа) 
f
L(E,µ)
и 
=cµE,
µE<+∞.
3)
f,g: E→
– неотрицательные измер. ф-ии на E и
x
E
0≤f(x)≤g(x)
и g
L(E,µ)
f
L(E,µ)
и
4)
Пусть f: E→R – измер. функция и f
L(E,µ),
c
R
cf–интегри-ма по Лебугу, т.е cf
L(E,µ)
и
.
5) Пусть f: E→R – измер-ма и огр., , µE<+∞. f L(E,µ) и µEinf(f).
6)
f: E→R – измер-ма и неотр. f
L(E,µ) и A
α,А
E
L(E,µ)
и .
7)
Пусть f интегр. По лебегу на множ. X по
мере µ (т.е. f
L(E,µ)), A,B
α,
A
B=
.
8)
Интеграл Лебега не зависит от значений
функций на множ. Меры ноль. Пусть f
L(E,µ), E
α,
B
E(µB)=0
9)
Пусть ф-ия f
L(E,µ) и g: E→R – измеримая и f=g почти всюду
на E
и
.
10)
f
L(E,µ)
│f│
L(E,µ).
11) Пусть f – интегр по Лебегу на множ. E, то ф-ия f почти всюду конечна.
12)
(сво-во аддитивности инт.) Пусть f=f1+f2,
где fi
L(E,µ), i=1,2. Тогда f
L(E,µ) и
.