Основные свойства решений линейных дифференциальных уравнений. Линейные дифференциальные уравнения с постоянными коэффициентами.
Принцип суперпозиции основан на следующих свойствах решений линейных дифференциальных уравнений.
1. Если y1(x) иy2(x)— два решения линейного однородного дифференциального уравнения
y(n)+an-1(x)y(n - 1)+ ... +a1(x)y' +a0(x)y= 0
то любая их линейная комбинация y(x) =C1y1(x) +C2y2(x)яв-ся решением этого однородного ур-ния.
2. Если y1(x) иy2(x)— два решения линейного неоднородного уравнения L(y) =f(x), то их разность y(x) =y1(x) −y2(x)яв-ся решением однородного ур-нияL(y) = 0.
3. Любое решение неоднородного линейного уравненияL(y) =f(x)есть сумма любого фиксированного (частного) решения неоднородного ур-ния и некоторого решения однородного ур-ния.
4. Еслиy1(x)иy2(x)— решения линейных неоднородных ур-ний L(y) =f1(x)иL(y) =f2(x)соответственно, то их суммаy(x) =y1(x) +y2(x)яв-ся решением неоднородного ур-ния L(y) =f1(x) +f2(x).
Св-ва решений однородного лин. ур-ния. Решения однородного линейного ур-ния обладают следующими двумя характерными для этого уравнения св-ми.
1.
Если
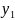есть частное решение ур-ния у'+р(х)у=0(*),
т. е. имеет место тождество
'+р(х)
=0 (а<х<b)
(1), то функцияУ = С
(2),
где С — произвольная постоянная, тоже
яв-ся решением этогоур-ния.
Действительно,
полагая в левой части ур-ния (*) у=С
и
принимая во внимание тождество (21),
получим:(С
'
+ р(х)(С
= С [
-
р(х)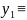
0
(а<х<b). (3)
Следовательно, у = С есть решение уравнения (*).
2.
Если
—
ненулевое частное решение уравнения
(*), тоформула (22), где С — произвольная
постоянная, дает общее решение ур-ния
(*) в области 0<x<b,-∞<y<+∞,
ур-ние
(22) разрешимо в области 0<x<b,-∞<y<+∞
относительно С:С =
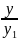(4),
и, как показано выше, ф-ция (2) является
решением ур-ния (*) при всех значениях
С. Следовательно, ф-ция (2)есть общее
решение ур-ния (*) в области 0<x<b,-∞<y<+∞.
Т.о., для построения общего решения однородноголин.Ур-ния достаточно найти какое-н одно ненулевое частное решение.
Структура общего решения лин. однородного ур-ний
Рассмотрим на[a;b]лин. однородное дифференциальное ур-ниеy(n)+an-1(x)y(n - 1)+ ... +a1(x)y' +a0(x)y= 0.(11)
Общим решением этого ур-ния на отрезке[a;b]наз. ф-цияy= Φ(x,C1,...,Cn),зависящая отnпроизвольных постоянныхC1,...,Cnи удовлетворяющая следующим условиям :−при любых допустимых значениях постоянныхC1,...,Cnф-цияy= Φ(x,C1,...,Cn)яв-ся решением ур-ния на[a;b];−какова бы ни была начальная точка(x0,y0,y1,0,...,yn − 1,0),x0∈ [a;b], существуют такие значенияC1=C10, ...,Cn=Cn0, что ф-цияy= Φ(x,C10, ...,Cn0)удовлетворяет начальным условиямy(x0) =y0,y '(x0) =y1,0,...,y(n − 1)(x0) =yn− 1,0.
Справедливо следующее утв-ие (теор о структуре общего решен.лин. однородного ур-ния).Если все коэффициенты ур-ниялин. однородного дифференциального ур-ниянепрерывны на отрезке[a;b], а ф-цииy1(x),y2(x),...,yn(x)образуют фундаментальную систему решенийэтого ур-ния, то общее решение ур-ния имеет вид
y(x,C1,...,Cn) =C1y1(x) +C2y2(x) + ... +Cnyn(x),(12), гдеC1,...,Cn— произвольные постоянные.
Структура общего решения линейного неоднородного уравнений
Всё тоже самое как и для однородного только вместо (11) и (12)=> формулы y(n)+an-1(x)y(n - 1)+ ... +a1(x)y' +a0(x)y=f(x). y(x,C1,...,Cn) =C1y1(x) +C2y2(x) + ... +Cnyn(x) +y*(x), гдеC1,...,Cn— произвольные постоянные,y*(x) — частное реш. неоднородного ур-ния. РЕШЕНИЕ ЛИНЕЙНОГО ОДНОРОДНОГО УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ МЕТОДОМ ЭЙЛЕРА |
Корни характеристического ур-ния лин. однородного дифференциального ур-ния с постоянными коэффициентами могут быть какдействительными, так икомплекснымичислами, могут бытьпростымиикратными.
Справедливы следующие утверждения.
Если числаλ1≠ λ2≠ ... ≠ λn— различные действительные корни характеристического ур-ния , то функцииexp(λ1x), exp(λ2x), ..., exp(λnx)образуютфундаментальную систему решенийур-ния.
Еслиλ = λ0— действительный корень характеристического ур-ния кратностиr,тоrф-цийexp( λ0x),xexp( λ0x),x2exp( λ0x), ...,xr-1exp( λ0x)—линейно независ.решения ур-ния.
Еслиλ = λ0= α ± βi—комплексно сопряженная пара корней характеристического ур-ния, то функцииexp( α x)cos(βx), exp( αx)sin(βx)— линейно независимые решения ур-ния.
Еслиλ = λ0= α ± βi—комплексно сопряженная пара корней характеристического ур-ния кратностиr, то2rфункцийexp( αx)cos(βx), exp( αx)sin(βx),xexp( αx)cos(βx),xexp( αx)sin(βx), ...,xr-1exp( αx)cos(βx),xr-1exp( αx)sin(βx)— линейно независ. решения ур-ния.