2. Двойной интеграл.

Пусть в обл Д зад огрн ф-я f(x,y). -частич обл Д, 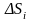-их площ. В кажд обл выб люб точку 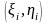. Сост сум -интегр сумм Римана. Рассм 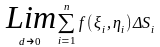(1), d- наиб из диаметров обл. разбиения, если этот Lim сущ и незав от спос разбиен Д на части, ни от выб точек, то гов: Df ф-я f(x,y) интегр по Риману в обл Д, а (1) наз двойным интегр от ф-и f(x,y) по обл Д и обоз

Условия существ дв инт: 1. Необх. Если ф-ция f(x,y) интегр в замкн огран квадрируем области, то она огран в этой обл. 2. Суммы Дарбу. Пусть ф-ция f(x,y) интегр в замкн огран квадрир обл Р и огран в Р. Произв. разбиение τ на n частей. Ф-ция огран в каждой из частич областей, т.е. по теор о существ точных верх и нижн граней можно сост суммы Дарбу: 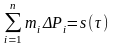и .

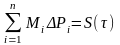Сведение двойного интеграла к повторному.

Вычисл двойн интегр м. свести к вычисл однократ.

1) прямоуг обл. Пусть обл интегр-я есть прямоуг Д={(x,y), a<=x<=b, c<=y<=d}, f непрер в нем. Если y фиксир-ть, то f будет ф-ей одног арг х, след 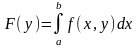. Зн-т F(y) м. интегр на [c,d]: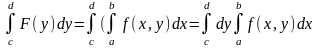

Терема: Пусть f(x,y) непрер в замк прямоуг Д, тогда

.

2)криволин-я обл. Д огран 2-мя непрер крив 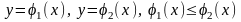и вертик пр x=a,x=b. ; если Д опред-ся нер-вом c<=y<=d, g1(y)<=x,=g2(y), где g1, g2-непрер на [c,d] ф-ии, то .

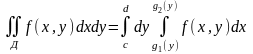Замена перем.

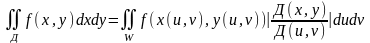
2. Теорема о существовании и единственности решения задачи Коши для обыкновенного ду первого порядка.

Рассмотрим обыкновенное ДУ 1–го порядка, записанное в нормальной форме:

Областью определения ур-ния называется область D определения правой части ур-ния f(x, y), D ⊂ R².

Ф-ция y=y(x) является решением задачи Коши

Если y=y(x) дифференцируема на [a, b], (x, y(x))∈D для всех x из [a, b], y(x₀)=y₀, x₀∈[a, b], и при подстановке в ур-ние обращает его в тождество:

Фундаментальным результатом теории обыкновенных ДУ является теорема существования и единственности решения задачи Коши:

Пусть ф-ция f(x, y) и ее частная производная f_y(x, y) непрерывны в некоторой области D плоскости x0y и точка (x₀, y₀) принадлежит области D.

Тогда:

— в некоторой окрестности (x₀−δ, x₀+δ) точки x₀ существует решение задачи Коши

— если y=φ₁(x) и y = φ₂(x) два решения задачи Коши, то φ₁(x)=φ₂(x) на (x₀−δ, x₀+δ).

Геометрически это означает, что если условия теоремы выполнены, то через каждую точку (x₀, y₀) области D проходит единственная интегральная кривая ур-ния.

Бесконечное множество решений ур-ния можно рассматривать как однопараметрическое семейство ф-ций y=φ(x; x₀) — семейство решений задачи Коши элементы которого различны для разных значений x₀. Иными словами область D "расслаивается" на интегральные кривые y=φ(x; x₀).

Важно понимать, что результат теоремы имеет локальный характер — существование и единственность решения гарантированы, вообще говоря, только в малой окрестности точки x₀. Важно также понимать, что условия теоремы существования и единственности достаточные условия. Нарушение условий теоремы не означает, что решение задачи не существует либо что оно не единственно.

2. Обыкновенные дифференциальные уравнения первого порядка, интегрируемые в квадратурах.

Ур-ние первого порядка имеет вид F(x,y,y')=0. Ур- ние, не содержащее искомой ф-ции в предположении, что его правая часть непр в инт (a,b), интегрируются в квадратурах. Его общ реш будет . Ур-ние с разделенными перем: 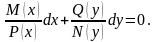Общ инт: ДУ с разделяющимися перем: M(x)N(y)dx+P(x)Q(y)dy=0. Одн ур-ния: 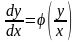. Вводим замену: z=y/x. ур-ние с раздел перемен. Общ инт: . Ур-ние M(x,y)dx+N(x,y)=0 наз обобщенным однор ур-нием, если сущ такое число к, при кот левая часть ур-ния становится однород ф-цией. При к=1 обобщ одн ур-ние явл обычным одн ур-нием. Делаем подстановку , где z-новая изв ф-ция, получаем ур-ние с раздел перемен. Общ инт: . Ур-ние вида y'+p(x)y=q(x) наз лин ДУ. Если q(x)=0, то ур-ние наз лин одн ДУ. 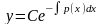-общ рещ. 1 метод: ( )(2). 2 метод: подстановка Бернулли: ищется реш ур-ния в виде двух ф-ций y=u(x)w(x). Подст в данное ур-ние: u'w+uw'+p(x)uw=q(x); u’w+u(w’+p(x)w)=q(x)(1);w'=-p(x)w; dw/w=-p(x)dx; 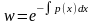. Подст в (1): Проинтегрируя получим y част неоднород, а потом и (2). Ур-ние Бернулли: 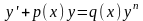. Разделим на 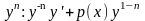=q(x). Замена: 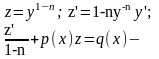лин ДУ. Ур-ние Рикатти: 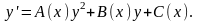Если известно одно частное реш данного ур-ния, то оно имеет общ реш. ДУ вида M(x,y)dx+N(x,y)dy=0 (1) наз ур-нием в полных диференц, если Если левую часть (1) свернуть dv(x,y)=0, то v(x,y)=C. 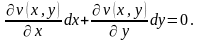Дифференциал ф-ции двух перемен: 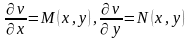Возьмем частную произв по у в первом и по х во втором: 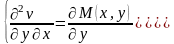Если смеш произв будут = 0, то и правые части будут =. Как находим: 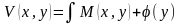Дифференцируем M(x,y): 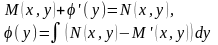Потом находим V(x,y). Ф-цию 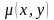наз интегрирующим множит ДУ 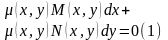, если при умножении на это ур- ние она обращ его в полн диференциал. 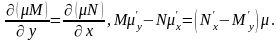Это лин ДУ 1 порядка с двумя неизв. 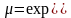1) если мю зависит от х, то: ; 2) если мю зависит от у, то