
- •Ограниченные числовые множества. Существование точных граней.
- •Предел числовой последовательности.
- •Существование предела последовательности.
- •Предел функции в точке.
- •Основные теоремы о пределах.
- •Непрерывность функции в точке. Свойства непрерывных функций.
- •Дифференцируемость функции в точке. Производная и дифференциал.
- •Основные теоремы дифференциального исчисления.
- •Приложения дифференциального исчисления к исследованию ф-ции.
- •Интеграл Римана и его свойства.
- •Приложения интеграла Римана.
- •Дифференцирование функций многих переменных.
- •Основные теоремы о дифференцировании функций многих переменных.
- •Числовые ряды.
- •Функциональные последовательности.
- •Функциональные ряды.
- •Тройной интеграл.
- •Двойной интеграл.
- •Теорема о существовании и единственности решения задачи Коши для обыкновенного ду первого порядка.
- •Обыкновенные дифференциальные уравнения первого порядка, интегрируемые в квадратурах.
- •Основные свойства решений линейных дифференциальных уравнений. Линейные дифференциальные уравнения с постоянными коэффициентами.
- •Множества, измеримые по Лебегу на прямой. Их свойства.
- •Сравнение интеграла Римана с интегралом Лебега.
- •Дифференцируемость функции комплексной переменной (фкп).
- •Интеграл от функции комплексной переменной.
- •Группы. Примеры групп. Простейшие свойства группы. Подгруппы. Гомоморфизмы и изоморфизмы групп.
- •Кольцо. Примеры колец. Простейшие свойства кольца. Подкольцо. Гомоморфизмы и изоморфизмы колец.
- •Поле. Простейшие свойства поля. Поле q. Поле с.
- •Векторное пространство. Базис и размерность конечномерного векторного пространства. Подпространства. Линейные многообразия. Изоморфизмы векторных пространств.
- •Многочлены от одной переменной над полем. Производная многочленов. Нод двух многочленов и алгоритм Евклида. Неприводимые многочлены.
- •Многочлены над полями с, r и q. Многочлены от n переменных. Алгебраические и трансцендентные числа.
- •Отношение делимости в кольце целых чисел.
- •Отношение сравнения в кольце целых чисел.
- •Аксиоматические теории и схема их построения. Построение системы натуральных чисел.
- •Построение системы целых чисел. Операции на множестве целых чисел и их свойства. Система рациональных чисел.
- •Плоскость Лобачевского. Аксиома Лобачевского. Аксиома Лобачевского и простейшие следствия из нее. Взаимное расположение прямых на плоскости Лобачевского.
- •Трехмерное евклидово пространство. Векторное произведение векторов. П риложения к решению задач.
- •Взаимное расположение двух плоскостей, прямой и плоскости, двух прямых в трехмерном пространстве.
- •Трехмерное евклидово пространство. Смешанное произведение векторов. Приложения к решению задач.
- •Полярные координаты. Простейшие задачи в полярных координатах. Уравнение линии. Эллипс, гипербола и парабола в полярных координатах.
- •Проективная плоскость и ее модели. Проективные свойства фигур. Группа проективных преобразований плоскости. Приложения к решению задач.
- •Параллельное проектирование и его свойства. Изображение плоских и пространственных фигур в параллельной проекции. Позиционные задачи.
- •Графы. Виды графов, способы их задания. Числовые характеристики графов.
- •Основные понятия и формулы комбинаторики.
- •Элементы логики высказ, математической логики и логики предикатов.
- •Бинарное отношение. Отображения, обратное отображение. Отношения эквивалентности и порядка. Фактор–множество.
- •Кривые в трёхмерном евклидовом пространстве. Касательная, нормальная и соприкасающаяся плоскость кривой. Канонический репер кривой. Кривизна и кручение кривой.
- •Поверхности в трёхмерном евклидовом пространстве. Касательная плоскость и нормаль к поверхности. Первая и вторая квадратичные формы поверхности и их применение.
- •Методы научного познания в обучении математике.
- •Методика изучения математических понятий.
- •Методика изучения математических предложений.
- •Задачи в школьном курсе математики.
- •Методика изучения числовых множеств в школьном курсе математики.
- •Методика изучения тождественных преобразований выражений в школьном курсе математики.
- •Понятие функции. Методика изучения алгебраических функций в школьном курсе математики. Функции натурального аргумента.
- •Методика изучения трансцендентных функций в школьном курсе.
- •Методика изучения производной. Применение производной в школьном курсе математики.
- •Методика решения трансцендентных уравнений, неравенств и их систем.
- •1.Тригонометрические уравнения. Содержание и методика.
- •Методика изучения начал систематического школьного курса планиметрии.
- •Методика изучения четырехугольников, их свойств.
- •Методика изучения величин в школьном курсе планиметрии.
- •Методика изучения основных соотношений между элементами треугольника.
- •Методика изучения подобия фигур.
- •Методика формирования у учащихся навыков решения задач по планиметрии. Обучение школьников решению задач на построение циркулем и линейкой.
- •Методика изучения первых разделов систематического курса стереометрии. Особенности методики работы с многогранниками.
- •Методика изучения взаимного расположения прямых и плоскостей в пространстве.
- •Методика обучения учащихся нахождению углов и расстояний в пространстве.
- •Методика изучения многогранников и их свойств.
- •Методика изучения тел вращения, их св-в.
- •Методика изучения площадей поверхностей и объемов многогранников и тел вращения.
- •Методика обучения школьников решению задач на комбинации многогранников и тел вращения.
Ограниченные числовые множества. Существование точных граней.
Мн-во есть неопределяемое, первичное понятие, которое подразумевает совокупность строго определенных эл-тов.
Основные характкристики мн-в.
Мн-во представляет собой набор (совокупность) некоторых элементов.
Для каждого математ. объекта имеется возможность точно установить, является ли он элементом данного мн-ва или нет.
Для двух элементов мн-ва всегда известно, совпадают они или нет.
При этом данные св-ва не являются определением того, что такое мн-во, они скорее говорят о том, какие совокупности нельзя считать мн-ми. Для стандартных, часто используемых мн-в есть стандартные обозначения: N, Z, Q, R - мн-ва натуральных, целых, рациональных и действительных чисел.
Опр. Пустое мн-во – мн-во не содержащее ни одного элемента.
Опр. Числовое мн-во – это мн-во элементами которого явл числа.
Опр.
Мн-во X
назовем ограниченным сверху (снизу),
если
МR
(
mR),
такое что xX
справедливо соотношение x
M
(x
m).Число
M
и m
наз. Границами числового мн-ва
соответственно верхней и нижней.
Наибольшую из всех нижних границ наз.
точной нижней гранью мн-ва X
и обозн.
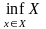 .
Наименьшую из всех верхних границ наз.
точной верхней гранью мн-ва X
и обозн.
.
Наименьшую из всех верхних границ наз.
точной верхней гранью мн-ва X
и обозн.
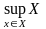 .
.
Опр. Мн-во XR наз. ограниченным если оно ограниченно сверху и снизу или СR(С>0), что xX справедливо нер-во xC.
Т. Если мн-во R состоит хотя бы из одного элем. и ограниченно сверху (снизу), то существ такие числа из мн-ва R которые явл точной верхней (точной нижней) гранью.
Предел числовой последовательности.
Пусть ф-ция f(x) задана на множестве N. Запишем значение ф-ции в порядке возрастания номера аргумента f(1),f(2),...,f(n),...
Опр.Числовая ф-ция f(x) задана на мн-ве N наз. числовой последовательностью f(1)=x1, f(2)=x2, ..., f(n)=xn,... , x1,x2,...,xn , если n зафиксированное , то xn наз. n-ым членом числовой последовательности. Если n переменная величина, то xn наз. общим членом данной последовательности.
Опр.Действительное число а наз. пределом числовой последовательности если 0 n0N, что n>n0(nN) xn-a<.
На языке окрестности определение предела имеет вид: U(a) Un0(+), что n>Un0(+) xnU(a).
Число а не явл пределом числовой последовательности если, 0, что nN мы можем указать такой n> n xn-a. Последовательность имеющая конечный предел ныз. сходящейся, в противном случае расходящейся.
Lim xn=- (n+)
(Е- сколь угодно большое)
Опр. Е>0, n0N , n>n0 xn<-E.
На языке окрестности: U(a) Un0(+), что n>Un0(+) xnUE(-).
Lim xn= (n+)
Опр. Е>0, n0N , n>n0 xn>E.
На языке окрестности: U(a) Un0(+), что n>Un0(+) xnUЕ().
Опр.Действительное число а наз. предельной точкой мн-ва М если в любой проколотой окрестности точки а найдется хотя бы одна точка мн-ва М.
Кр. Предельной точки. Действительное число а явл. предельной точкой мн-ва М когда из мн-ва М можно выделить послдовательность элементов отличных друг от друга и от точки а, такую чтобы сходилась в точке а.
Т. Если числовая последовательность имеет предел, то он единственный.
Док-во: Пусть существует два предела а,b числ. последоват. xn.
Lim xn=а (n+) по опр. 0 n0N, что n>n0 xn-a</2. (1)
Lim xn=b (n+) по опр. 0 n0N, что n>n0 xn-b</2. (2)
Выберем в качестве n0 max знач. Из n0 и n0, тогда n>n0 оба неравенства (1) и (2) будут выполняться одновременно. Раз это так оценим 0b-a=b-xn+xn-ab-xn+xn-a2+=. Отсюда следует b-a=0, зн. b=a. Ч.т.д.
Последовательность
![]() ,
предел которой равен нулю
,
предел которой равен нулю
![]() ,
наз бесконечно
малой.
,
наз бесконечно
малой.
Последовательность
![]() называется
бесконечно
большой,
если для любого положительного числа
называется
бесконечно
большой,
если для любого положительного числа
![]() ,
как бы велико оно ни было, существует
такой номер N,
что для всех
с
номерами
,
как бы велико оно ни было, существует
такой номер N,
что для всех
с
номерами![]() справедливо
неравенство
справедливо
неравенство
![]() ,
записываем
,
записываем
![]()
Необходимый
и достаточный признак сходимости
монотонной последовательности:
Монотонная последовательность сходится
тогда и только тогда, когда она ограничена.
Критерий
Коши:
Последовательность сходится тогда и
только тогда , когда
![]() (не
используется само значение предела!)
(не
используется само значение предела!)
Число e. Т. Последовательность xn=(1+1/n)n nN сходится.
