Правила контроля правильности эпюр q и m (Qy и Mx)

1. Эпюра Q_y является прямолинейной на всех участках.

2. Эпюра M (M_x) является криволинейной (квадратная парабола) на участке под равномерно распределенной нагрузкой1, и прямолинейная на всех остальных участках.

3. Под точкой приложения сосредоточенной силы (реакции) на эпюре Q_y обязательно должен быть скачок (разрыв) на величину этой силы (реакции). Аналогично, под точкой приложения сосредоточенного момента на эпюре M_x обязательно будет скачок на величину момента.

4. Если на участке под распределенной нагрузкой эпюра Q_y пересекает ось, то эпюра M_x в этом сечении имеет экстремум.

5. На участках с поперечной силой одного знака эпюра моментов M_x имеет одинаковую монотонность. Так, если Q_y > 0 эпюра моментов убывает2 слева направо; при Q_y > 0 эпюра M_x возрастает слева направо.

6. Порядок линии на эпюре Q_y всегда на единицу меньше, чем на эпюре изгибающих моментов. То есть, если эпюра моментов M_x – квадратная парабола, то эпюра поперечных сил Q_y на этом участке – наклонная прямая; если эпюра M_x – наклонная прямая, то эпюра Q_y на этом участке – прямая, параллельная оси; если M_x постоянная (прямая, параллельная оси), то на этом участке Q_y = 0.

Правило знаков для поперечной силы

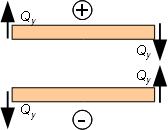Поперечная сила считается положительной, если она стремится повернуть элемент балки по ходу часовой стрелки. При построении эпюры поперечной силы положительные значения поперечной силы откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.

7. Определение внутренних усилий и напряжений в поперечных сечениях стержней при центральном растяжении-сжатии. Метод сечений. Эпюры.

8.Нормальные напряжения в поперечных сечениях балок. Нормальные и касательные напряжения при поперечном изгибе

Нормальные И Касательные Напряжения При Поперечном Изгибе Сопромат

При поперечном изгибе в сечении балки помимо изгибающего момента ( )возникает поперечная сила ( ). Поэтому в поперечном сечении при поперечном изгибе наряду с нормальными напряжениями ( ) возникают и касательные напряжения ( ).

На основании закона парности касательные напряжения возникают и в продольных сечениях балки. Вследствие этого при поперечном изгибеотмечаются сдвиги продольных слоев балки относительно друг друга.

При поперечном изгибе гипотеза плоских сечений нарушается, поскольку поперечные сечения балки искривляются (рис. 7.9).

Исследования показали: если балка является достаточно длинной, влияние искривления поперечного сечения на значения нормальных напряжений невелико, поэтому влиянием сдвигов на закон распределения нормальных напряжений при изгибе пренебрегают, формула нормальных напряжений при поперечном изгибе:  .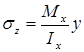

Проанализируем формулу Журавского:

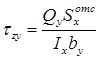
Поперечная сила ( ) для конкретного сечения и момент инерции поперечного сечения относительно нейтральной оси  являются постоянными величинами, поэтому касательные напряжения изменяются по высоте поперечного сечения по тому же закону, что и отношение статического момента отсеченной части поперечного сечения ( ) к ширине поперечного сечения ( ), в котором они вычисляются.

Во всех точках поперечного сечения, расположенных на расстоянии y отнейтральной линии (по всей ширине сечения  ), касательные напряжения при поперечном изгибе одинаковы.

В самых удаленных от нейтральной оси точках поперечного сечения касательные напряжения при поперечном изгибе равны 0, поскольку в этом случае  .

Наибольшие касательные напряжения возникают в точках поперечного сечения, расположенных на нейтральной оси. Напомним, что в этих точках нормальные напряжения равны нулю