- •Сопротивление материалов: общие положения. Термины: деформация, внутренние усилия, прочность, жесткость, устойчивость, упругость, пластичность.
- •Условия прочности балок. Методика подбора размеров поперечных сечений для балок.
- •Классификация элементов конструкций и сооружений.
- •Изгибаемые стержни (балки): общая схема деформирования, расчетные схемы, классификация.
- •5. Принципы определения реакций в опорных устройствах конструкций
- •Внутренние усилия в поперечных сечениях балок, правила знаков, построение эпюр. Общий ход определения усилий и построения эпюр
- •Правила контроля правильности эпюр q и m (Qy и Mx)
- •Определение внутренних усилий и напряжений в поперечных сечениях стержней при центральном растяжении-сжатии. Метод сечений. Эпюры.
- •8.Нормальные напряжения в поперечных сечениях балок. Нормальные и касательные напряжения при поперечном изгибе
- •9. Продольные деформации при центральном растяжении-сжатии. Закон Гука
- •Механические характеристики сопротивления растяжению-сжатию различных материалов. Диаграммы деформирования.
- •Оптимальная форма поперечного сечения для балок при плоском прямом изгибе ответа нет
- •21. Площади поперечных сечений стержней различных конфигураций. Принципы их определения.
- •22. Зависимость между напряжениями и деформациями при плоском и объемном напряженном состояниях (обобщенный закон Гука). Коэффициент относительного изменения объема.
- •23. Внутренние силы. Метод сечений.
- •24. Неразрезные балки. Уравнение трех моментов.
- •5. Зависимость между моментами инерции относительно параллельных осей
- •26) Чистый сдвиг. Закон Гука при сдвиге. Условие прочности. Простейшие расчеты на срез.
- •Задача и методы сопротивления материалов.
- •Деформации упругие и пластические
- •Типы деформаций
- •Статические моменты площадей сечений стержней. Определение положения центра тяжести площади плоской фигуры.
- •Статически неопределимые задачи растяжения и сжатия стержней Понятие статической неопределимости.
- •Один из общих методов решения статически неопределимых задач.
- •33.Расчёты на прочности при растяжении и сжатии
- •34. Назначение гипотез на прочность
- •35. Деформация при растяжении и сжатии. Закон Гука
- •36. Общее понятие об изгибе
- •41. Радиусы инерции площадей плоских фигур
- •42. Условия жесткости балок
- •49. Контроль правильности построения эпюр поперечной силы и изгибающего момента. Примеры.
- •Построение эпюр поперечных сил и изгибающих моментов Определение поперечных сил и изгибающих моментов - сечение 1
- •50 Чистый сдвиг.
41. Радиусы инерции площадей плоских фигур
Радиусом инерции плоской фигуры относительно какой-либо оси, называется длина перпендикуляра, отсчитываемая от этой оси и вычисляемая по формуле:
![]()
![]() (18)
(18)
![]()
![]()
42. Условия жесткости балок
|
Условие жесткости по логике строится так же, как и условие прочности. Однако, ограничения накладываются не на напряжения, а на изменение формы стержня (вала, балки), т.е. деформации. Для разных видов нагружения условия жесткости имеют вид: при растяжении (сжатии) |
|
|
|
при кручении |
|
|
|
где |
|
при изгибе |
|
|
|
где
43.растяжение и сжатие. продольная сила и ее эпюра
Растяжение и сжатие Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор -продольная сила. Продольные силы меняются по длине бруса. При расчётах после определения величин продольных сил по сечениям строится график - эпюра продольных сил. Условно назначают знак продольной силы Если продольная сила направлена от сечения, то брус растянут. Растяжение считают положительной деформацией. Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией. Эпюрой продольной силы называется график распределения продольной силы вдоль от бруса. Ось эпюры параллельна продольной оси. Нулевая линия проводится тонкой линией. Значения чисел откладывают от оси, положительные - вверх, отрицательные вниз. В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz. Правило контроля: в месте приложения внешней силы на эпюре должен быть скачек на величину приложенной силы. На эпюре проставляют значения Nz. Величины продольных сил откладывают в заранее выбранном масштабе. Эпюра по контуру обводится толстой линией и обводится поперёк оси. Принцип смягчения граничных условий гласит: в точках тела, удалённых от мест нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.
44. Метод сил. Выбор основной и эквивалентной системы
Наиболее широко применяемым в машиностроении общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Отсюда и название «метод сил». Такой прием не является единственно возможным. В строительной механике широко применяются и другие методы, например метод деформаций, в котором за неизвестные принимаются не силовые факторы, а перемещения в элементах стержневой системы.
Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы. |
|
|
Основная система, к которой приложены все внешние заданные силы и неизвестные силовые факторы, носит название эквивалентной системы.
45. Определение внутренних усилий при изгибе
При определении внутренних усилий при изгибе пользуются следующими принципами,
являющимися следствиями реализации метода сечений:
1. Поперечная сила Q в сечении балки численно равна алгебраической сумме
проекций на плоскость сечения всех внешних сил, действующих по одну сторону от
сечения.
2. Изгибающий момент М, возникающий в поперечном сечении балки, численно
равен алгебраической сумме моментов внешних сил, действующих по одну сторону от
данного сечения, относительно этого сечения.
Правило знаков:
- поперечная сила в сечении балки считается положительной, если равнодействующая
внешних сил, действующих слева от сечения, направлена снизу вверх, а действующих
справа от сечения - сверху вниз, и отрицательной - в противоположных случаях;
- изгибающий момент считается положительным, если в рассматриваемом сечении
балка изгибается выпуклостью вниз, и отрицательным- в противоположном случае
(рис 11).

Эпюрой изгибающих моментов МИ или поперечных сил Q называется графическое
изображение зависимости соответствующего внутреннего силового фактора от
координаты сечения, откладываемой вдоль оси балки.
46. Внецентренное растяжение-сжатие стержня (в сопротивлении материалов), деформация, возникающая при действии на стержень двух равных и противоположно направленных продольных сил, параллельных оси стержня; один из видов сложного сопротивления. В. р.-с. характеризуется сложением деформаций от изгиба и от продольных сил. При В. р.-с. в точках поперечного сечения с текущими координатами у и z, взятыми относительно главных центральных осей (рис.), нормальные напряжения определяются по формуле:
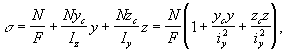
в которой F — площадь поперечного сечения, Iy и Iz— моменты инерции сечения, iy и iz — радиусы инерции сечения, ус и zc — координаты точки приложения продольной силы N. Нормальные напряжения линейно зависят от координат и достигают максимальных значений в точках поперечного сечения, наиболее удалённых от нейтральной линии, положение которой определяется отрезками ау и az, отсекаемыми на координатных осях:
![]()
Если продольная сила приложена в границах ядра сечения, то нейтральная линия либо лежит за пределами сечения, либо касается контура сечения, при этом эпюра нормальных напряжений становится однозначной. Случаи В. р.-с. часто встречаются при расчётах фундаментов, арок, рам и других конструкций.
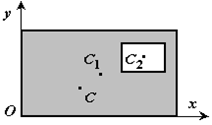
47.Статические моменты площадей сечений стержней. Определение положения центра тяжести площади плоской фигуры. Способы определения координат центра тяжести 1 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1 + S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны
Рисунок 1.8
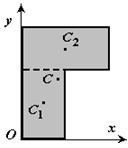
2 Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.9
Рассмотрим
поперечное сечение стержня площадью
F. Проведем через произвольную точку
О оси координат x и y. Выделим элемент
площади
В
Аналогично статический момент инерции относительно оси y равен:
Просуммировав такие произведения по площади F, получим статический момент инерции всей фигуры относительно осей x и y:
Статический момент инерции фигуры относительно оси измеряется в единицах длины в кубе (см3), и может быть положительным, отрицательным и равным нулю.
Пусть
Таким образом, моментом (статическим моментом) площади фигуры относительно оси называется произведение площади на расстояние от ее центра тяжести до оси.
48.Понятие о косом изгибе. Определение напряжений и деформаций. Косой изгиб – изгиб, при котором плоскость P действия изгибающих моментов и поперечных сил не совпадает ни с одной из главных плоскостей инерции бруса.
Используя принцип независимости действия сил (принцип суперпозиции) найдем напряжения при косом изгибе. Рассмотрим точку A с координатами (y, z) в сечении изгибаемой балки и определим в ней напряжения от каждого из внутренних усилий, возникающих при косом изгибе: -нормальные
напряжения от изгибающего момента M
z:
-нормальные
напряжения от изгибающего момента
My
:
-касательные
напряжения от поперечной силы Qy
:
-касательные
напряжения от поперечной силы
Qz
:
-Полные напряжения
а) касательных: б) нормальных:
Последнюю формулу
удобно представить в виде:
Или:
где
Полное
перемещение
при косом изгибе определяют через
перемещения в направлениях главных
центральных осей δx и
δy:
Перемещение
по направлению оси x находим методом
Мора:
Аналогично,
перемещение по направлению оси y:
От
сюда Полное перемещение:
Расчет прочности. -для форм поперечного сечения, как круг и все правильные многоугольники, у которых все центральные оси – главные, случай косого изгиба невозможен. Для таких сечений условие прочности можно записать следующим образом:
где
-для
круглого сечения . -для квадратного сечения условие прочности может быть записано в том же виде, что и для прямоугольного. |
|
- для сечения произвольной формы
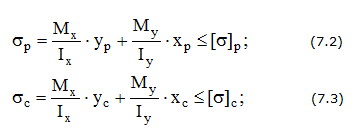
- для сечений типа прямоугольник, двутавр, швеллер


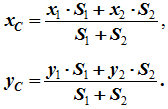
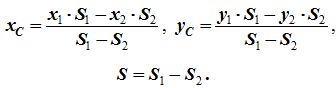
 ведем
понятие статического момента инерции
относительно оси - величину, равную
произведению элемента площади (
)
на расстояние (обозначено буквой y) до
оси x:
ведем
понятие статического момента инерции
относительно оси - величину, равную
произведению элемента площади (
)
на расстояние (обозначено буквой y) до
оси x: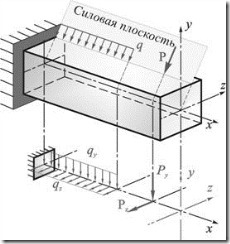 Определение
напряжений при косом изгибе
Определение
напряжений при косом изгибе




 и
и
 при косом изгибе найдем путем
геометрического суммирования
составляющих:
при косом изгибе найдем путем
геометрического суммирования
составляющих:


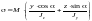
 – угол наклона силовой плоскости P
при косом
изгибе (а при сложном
изгибе
– угол наклона плоскости действия
полного изгибающего момента M
в данном сечении. (Нейтральная ось -
геометрическое место точек, в которых
продольные нормальные напряжения
равны нулю.)
– угол наклона силовой плоскости P
при косом
изгибе (а при сложном
изгибе
– угол наклона плоскости действия
полного изгибающего момента M
в данном сечении. (Нейтральная ось -
геометрическое место точек, в которых
продольные нормальные напряжения
равны нулю.)


 ,
,