35. Деформация при растяжении и сжатии. Закон Гука

Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.

В словесной форме закон звучит следующим образом:

Сила упругости, возникающая в теле при его деформации, направлена против смещения частиц тела при деформации и прямо пропорциональна удлинению.

Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь   — сила, которой растягивают (сжимают) стержень,   — абсолютное удлинение (сжатие) стержня, а   — коэффициент упругости (или жёсткости).

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения   и длины  ) явно, записав коэффициент упругости как

Величина   называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.

Если ввести относительное удлинение

и нормальное напряжение в поперечном сечении

то закон Гука для относительных величин запишется как

В такой форме он справедлив для любых малых объёмов материала.

Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

Коэффициент Пуассона (обозначается как   или  ) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала.

При приложении к телу растягивающего усилия оно начинает удлиняться в продольном направлении, а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз относительное уменьшение поперечного размера деформируемого тела больше относительного увеличения его длины, при его растяжении. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно несжимаемого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5.

36. Общее понятие об изгибе

Изгиб — вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов. Прямой изгиб возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, называется косым.

Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб.

Часто термин «прямой» в названии прямого чистого и прямого поперечного изгиба не употребляют и их называют соответственно чистым изгибом и поперечным изгибом

 Изгибающий момент, поперечная сила и интенсивность распределенной нагрузки связаны следующими зависимостями (зависимостями Д.Н.Журавского):

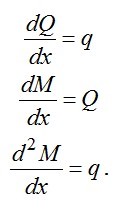   . Выводы:

1 Если на некотором участке балки отсутствуюет распределенная нагрузка (q=0), то  эпюра Q – прямая, параллельная к оси абсцисс (Q=const), а эпюра М на этом участке наклонная прямая.

 2 Если на некотором участке есть равномерно распределенная нагрузка, то эпюра Q – наклонная прямая, параллельная оси абсцисс (Q=const), а эпюра М – парабола

3 Если на некотором участке балки: Q > 0, то изгибающий момент возрастает, Q < 0, то изгибающий момент убывает, Q = 0, то изгибающий момент постоянный

4 Если поперечная сила, изменяясь по линейному закону, проходит через нулевое значение, то в соответствующем сечении изгибающий момент будет иметь экстремум.

5 Под сосредоточенной силой на эпюре Q образуется прыжок на величину приложенной силы, а на эпюру М – резкое изменение угла наклона соседних участков.

6 В сечении, где приложена пара сил, эпюра М будет иметь прыжок на величину момента пары. На эпюре Q это не отразиться.

7 Если равномерно распределенная нагрузка  направлена вниз (вторая производная, которая характеризует кривизну линии),  эпюра М обращена выпуклостью вверх, навстречу нагрузке.

37.

3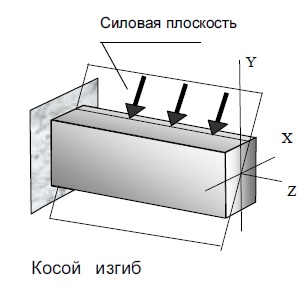 8. Сложное сопротивление. Под сложным сопротивлением понимают различные комбинации простых напряженных состояний (растяжения, сжатия, сдвига, кручения, изгиба). В общем случае в поперечных сечениях бруса действуют шесть компонентов внутренних усилий: N, Qx, Qy, Mx, My, Mz=Mкр. Нормальная сила N и изгибающие моменты Mx, My вызывают нормальные напряжения. От поперечных сил Qx, Qy и крутящего момента Mz=Mкр возникают касательные напряжения.

Косым изгибом называется такой случай изгиба, когда плоскость, в которой располагается внешняя нагрузка (силовая плоскость), не совпадает ни с одной главной плоскостью балки. Внешнюю нагрузку при косом изгибе можно разложить на вертикальную и горизонтальную составляющие. Поэтому косой изгиб можно рассматри-

вать как одновременный изгиб балки в двух главных плоскостях.

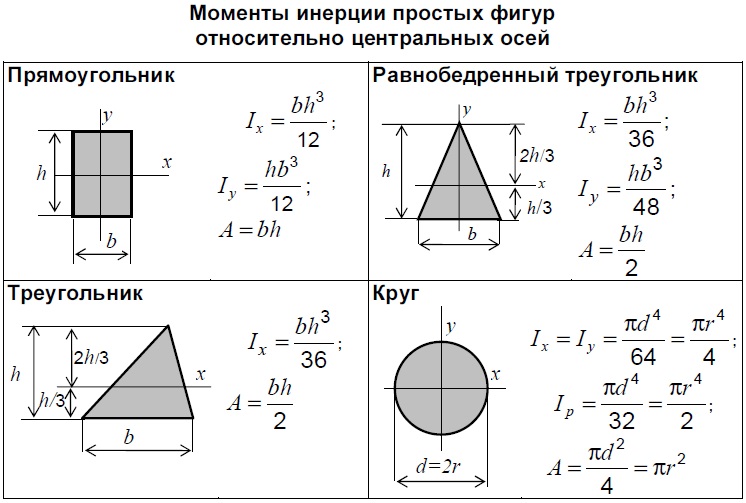
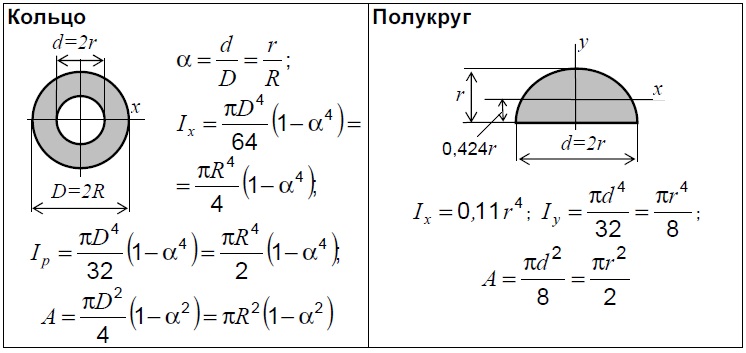
39. Среди осей, проходящих через центр тяжести площади, есть такие взаимно-перпендикулярные оси, относительно которых осевые моменты инерции принимают экстремальные значения, а центробежный момент инерции равен нулю. Такие оси называются главными центральными осями, а моменты инерции относительно этих осей – главными центральными моментами инерции. Если известны моменты инерции площади относительно произвольных осей I_x , I_y , I_xy , то главные моменты инерции I_max , I_min вычисляют по формуле

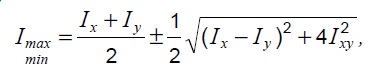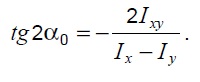а угол a₀ между осью x и главной осью u (I_u = I_max , I_v = I_min определяют через тангенс двойного угла

40.

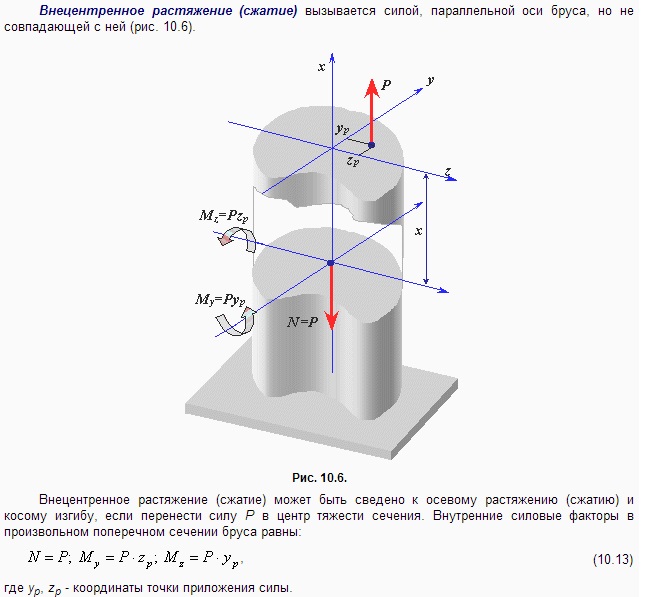
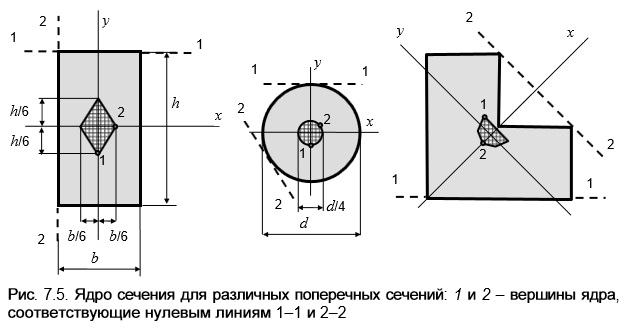
Ядром сечения называется замкнутая выпуклая область вокруг центра тяжести , при нахождении силы F внутри которой или на её границе во всех точках поперечного сечения возникают напряжения одного знака (рис . 7.5).

Перемещения и деформации. Под действием внешних сил твердые тела изменяют свою геометрическую форму, а точки тела неодинаково перемещаются в пространстве. Вектор , имеющий свое начало в точке А недеформированного состояния, а конец в т. деформированного состояния, называется вектором полного перемещения т. А. Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, v и w, соответственно.

Допустимым (допускаемым) напряжением называется величина, ограничивающая верхний предел рабочих напряжений возникающих под действием заданных нагрузок. Обозначаются [σ] – нормальные и [τ] – касательные д.н.

Рассчитывается по формуле:

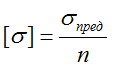
где

σ_пред – предельное напряжение, вызывающее разрушение элемента либо значительныеостаточные деформации.

Для пластичных материалов (сталь, бронза, латунь и т.д.) за предельное напряжение принимается предел текучести

σ_пред=σ_Т

Для хрупких материалов (чугун, цемент) предельным напряжением является предел прочности

σ_пред=σ_пч

n – нормативный запас прочности.

Запас прочности необходим для обеспечения бесперебойной работы элементов конструкций при непредвиденных временных перегрузках, возможных ошибках в расчетах либо вследствие изменений размеров элемента в процессе эксплуатации.