2.2.5 Построение гистограмм

Гистограмма является графическим способом представления информации. Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра.

Таким образом, гистограмма представляет собой графическое изображение зависимости частоты попадания элементов выборки от соответствующего интервала группировки. Ниже на рисунке 2.1, представлен пример гистограммы.

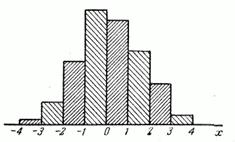
Рисунок 2.1 - Гистограмма.

Существует ряд популярных и широко используемых программ, которые содержат функции и алгоритмы, позволяющие графически строить гистограммы, а так же проводить различные численные операции над содержащими в них данными. Это такие программы как: SPSS – предоставляет широкие возможности для построения графиков и диаграмм, Microsoft Office Excel в котором можно создать гистограмму и придать ей привлекательный вид, STATISTICA – программа, предназначенная для статистического анализа и визуализации данных, а так же к ним относится программа Mathcad.

2.2.6 Гистограммы символьных последовательностей

После преобразовали измерений в строку символов, можно начать с характеристикой временных моделей. В этом направлении, вводится символические деревья и гистограммы последовательности символов. Символическое дерево представляет собой графическое представление статистики символов в зависимости от длины слов: вычисляется вероятность появления для различных слов в символической строке, а затем представляется это в дереве. [20] Первый уровень дерева является вероятностью появления символов, второй вероятностью возникновения словам двух символов и так далее. Символическое дерево представляет собой компактное краткое содержание информации о сигнале и каждого уровня дерева соответствует определенной длине последовательности символов. На рисунке 2.2 приведен пример дерева для двоичной символьной последовательности.

Рисунок 2.2- Символическое дерево

Для построения гистограммы последовательности символов, выберем последовательность символов длина 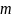, а затем вычисляем относительную частоту возникновения всех возможных последовательностей символов длины в полной последовательности символов. Если у нас есть разбиение штук (то есть , символов), мы должны вычислить относительную частоту всех 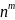слов символов, которые происходят в символической последовательности данных. Можем описать это как наблюдаемая динамика по гистограммам относительных частот. Для удобства и идентификации ,удобное представление каждого слова длины достигается путем преобразования последовательности базы в его десятичный эквивалент; например, если = 2 и = 4 мы будем иметь 16 = 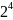различных слова длины 4, представленные каждого по ряду от 0 до 15 и, в частности слово 1101 представлено ​​число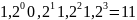 . Это представление называется кодовая последовательность и поможет в вычислении гистограммы и визуализации результатов. На рисунке 2.3 показано, гистограммы для символической последовательности рисунке 1 и = 2,3,4,5 .

Гистограммы последовательности символов являются компактными представлениями общей динамики временных рядов и могут использоваться для сравнения различных наборов данных[46]. С помощью этих частот можно выделить довольно равномерные распределения из более сложных. Это приводит к первой мере сложности системы, которая просто подсчитывает "запрещенные слова" (или для статистического подхода, число траекторий с низкой вероятностью возникновения). Также можно строить различные гистограммы для различных значений и сравнить их. Следует отметить, что когда работаем с равновероятными разбиениями, гистограммы последовательности символов могут быть использованы для количественного определения необратимости времени, потому что относительные частоты определенных последовательностей символов будут смещаться, когда данные соблюдаются в обратном времени. С другой стороны, для обратимого временного ряда, не должно быть никакого значительного различия в гистограмме, построена в прямом или обратном времени.

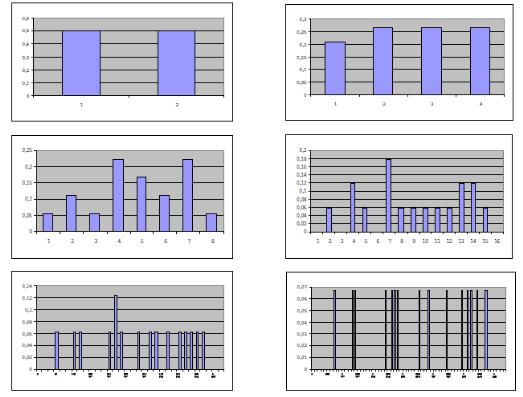
Рисунок 2.3 - Гистограммы = 1, 2, 3, 4, 5, 6 для символического временного ряда

Следующим шагом является введение некоторых статистических инструментов и информации теоретических мер для характеристики и сравнения их гистограмм:

1) Традиционное количество для характеристики последовательности символов является энтропия Шеннона. Энтропии Шеннона порядка 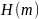на основе распределения последовательности вероятностей длины последовательности символов определяется по формуле (2.31)

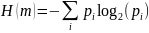(2.31)

Здесь 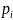является вероятностью нахождения i последовательности длины ( т. е. такое количество раз, что последовательность индексируется в долгосрочной символической последовательности, разделенной на число всех коротких последовательностей ). Это довольно абстрактное количество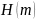 : измеряет среднее количество бит, необходимых для определения произвольной последовательности длины в символической последовательности. Это мера сложности или различный процесс, который генерирует последовательность. Когда есть хорошее разбиение, символический сигнал будет содержать в основном всю информацию, содержащуюся в исходном сигнале. Обратите внимание, что энтропия [3] Шеннона является показателем разнообразия: незаметная возможности не входит в меру и в относительном виде можно интерпретировать как показатель однородности ( аналогичной стандартного отклонения ). [20] Средняя вычисляется только для категорий наблюдений, которые эффективно возникают, и это находит свое отражение в . Кроме того, мы можем рассмотреть различия энтропии Шеннона

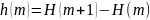(2.32)

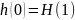(2.33)

Эти различия определяют количество информации, необходимой для определения 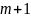символа произвольной последовательности заданного символической последовательностью, если первые символы известны. Энтропия Шеннона определяется как предел 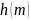по формуле (3.4)

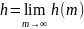(2.34)

Измененная (или нормализованная)энтропия Шеннона определяется по формуле (2.34)

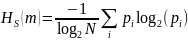(2.35)

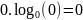где и где 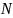является общим количество наблюдаемых последовательностей с длиной (т. е. количество последовательностей длины с ненулевой частотой), индекс для последовательностей длины и вероятность слова (т.е. слово построен по индексу ). Выбор логарифма 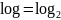отражает тот факт, что информация измеряется в битах. Очевидно 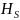есть нормированная форма и воспринимается как средняя неопределенность один символ.

Список некоторых полезных характеристик и интерпретаций различных типов энтропии:

1) Энтропия максимальна, когда вероятность разделяется поровну, и энтропия минимизируется, когда вероятность сосредоточена в одном компоненте. Другими словами, энтропия равна нулю, когда разнообразие наблюдений отсутствует, и максимальна, когда все категории занимают такое же количество наблюдений. В этом смысле Шеннона является мерой случайности.

2) Энтропия не реагирует на характер категорий, участвующих. Их метки свободно перестановочны: только набор частот. Именно в этом смысле, энтропия, как говорят, контекстно-свободна.

3) В отличии от дисперсии отклонений от среднего значения, которые предполагают нормальное распределение, энтропия не несет ничего о природе частоты или распределения вероятностей, она оценивает и разнообразные непараметрические меры и полностью вообще в этом отношении. Меры с этим свойством, как говорят, свободно распределены.

4) Энтропия представляет собой среднее: можно интерпретировать их как среднее число двоичных решений, принимаемых в процессе классификации.

5) Энтропия является функцией относительных величин, вероятность является наиболее распространенной формой. Размер образца не влияет на значения энтропии; именно по этой причине мы стандартизировали их выражения энтропии по отношению к их максимуму.

Значимое отклонение от равновероятности свидетельствует о временной зависимости и детерминированной структуры в данных. Для случайных данных и равновероятных имеет = 1 и для неслучайных данных, должен быть 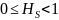и подразумевает более детерминированную структуру.

Характеристика последовательностей символов не ограничивается оценкой энтропии Шеннона. Широкий спектр так называемых мер сложности дает более подробную характеристику структуры этих последовательностей символов. Одно обобщение энтропии Шеннона энтропия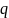 -Renyi определяется формулой (3.6)

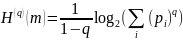(2.36)

где действительное число, 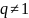. Этот показатель сходится к энтропии Шеннона при 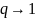. Из-за различных усреднений он отражает неоднородность исходного распределения вероятностей. Если 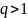последовательность длины с большой вероятностью преобладает над энтропией Renyi. Для 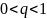имеем обратное.

Евклидова норма определяется формулой (3.7)

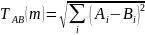(2.37)

и определяется по формуле (3.8)

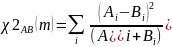(2.38)

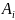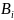где и представляют собой отдельные последовательности вероятности для возможных кодов последовательности и для гистограмм А и В. Статистические данные могут помочь, сравнить различные символические последовательности.

Евклидова норма работает как метрическая система в пространстве возможных последовательностей, обеспечивающая величину расстояния между различными гистограммами: большое расстояние между гистограммами следует, что динамика в наборе данных очень разная. Также 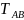может быть полезна при тестировании для обратимости времени на данных временных рядах путем сравнения гистограммы для временного ряда с поведением ее времени: размах евклидовой нормы между частотами гистограммы для прямого и обратного времени количественного уровеня необратимости времени. является производным от стандартного путем замены одномерной частоты измерений с частотами последовательности. Как и гистограмма последовательность символов, все эти статистические данные являются функциями последовательностей символов длины и нет никаких теоретических правил определяющих, какие достаточно или лучше для наблюдения существенных особенностей последовательности, если они существуют. [26]

В Daw, Finney и Green, есть эмпирический подход для выбора соответствующего с использованием измененной энтропии Шеннона. Они показывают, что , как правило, достигает минимального значения, как увеличена на 1. Объяснение этому минимуму в является то, что отражает преобразование символа последовательности, который наилучшим образом отличает данные из случайной последовательности. Символ последовательности, который слишком короткий, потеряет некоторые важные информационные и символьные последовательности, которые слишком долго отражают шум (то есть, нет достаточного количества данных, чтобы получить достоверные статистические данные для таких длинных последовательностей). Значение последовательности символов длиной , минимизирует измененную энтропию Шеннона и является «оптимальным» выбором для приведенных данных.