
- •Магистерская диссертация
- •230400.68 Информационные системы и технологии
- •230400.68.01 Информационно-управляющие системы
- •Глава 1. Информационно-аналитические технологии анализа данных……………………………………………………………………………...7 1.1 Роль и место информационно-аналитических систем…………7
- •Глава 2. Символьный анализ данных…………………………………..19
- •Глава 3. Применение символьного анализа в информационно аналитических системах......................................................................................57
- •Реферат
- •Введение
- •Глава 1. Информационно-аналитические технологии анализа данных
- •1.1 Роль и место информационно-аналитических систем
- •1.2 Технологии извлечения данных
- •Глава 2. Символьный анализ данных
- •Типы символьных данных
- •2.2 Гистограммы как символическое представление данных
- •2.2.1 Распределение данных
- •2.2.2 Обоснование гистограмм
- •2.2.3 Аппроксимация значений внутри каждого бакета
- •2.2.4 Анализ бинарных данных
- •2.2.5 Построение гистограмм
- •2.2.6 Гистограммы символьных последовательностей
- •2.4 Визуально интерактивные методы анализа данных
- •2.4.1 Теория Доу
- •2.4.2 Волновая теория Эллиотта
- •2.4.3 Метод японских свечей.
- •Глава 3. Применение символьного анализа в информационно аналитических системах
- •3.1.1 Одна зависимая переменная.
- •3.1.2 Многозначные переменная
- •3.1.3 Интервальные переменные
- •3.1.4 Гистограммные переменные
- •3.2 Кластерный анализ
- •3.2.1 Многозначные переменные
- •3.2.2 Интервальные переменные
- •3.3 Кластерный анализ в распознавании изображений
- •Заключение
- •Список использованных источников
- •Приложение а Исходный код программы распознавания изображений
2.2.3 Аппроксимация значений внутри каждого бакета
При заданном объеме пространства под гистограмму одним из основных компромиссов является сочетание числа бакетов и объема информации, сохраняемой в каждом бакете. Малый объем информации внутри каждого бакета влечет грубые локальные аппроксимации и большее число бакетов. Ключевым вопросом является нахождение правильного баланса в этом компромиссе для оптимизации общей аппроксимации распределения данных.
По отношению к аппроксимации [14] множества значений, попадающих в одномерный бакет, имеются два подхода. При традиционном предположении о непрерывности значений поддерживается наименьший объем информации (только минимальное и максимальное значения), но ничего такого, что могло бы каким-то образом подсказать, сколько значений имеется, и какими они могли бы быть. При использовании более современного предположения о равномерности промежутков также поддерживается число значений внутри каждого бакета, и реальное множество значений аппроксимируется множеством, формируемым путем (виртуального) размещения того же числа значений на равных расстояниях между минимальным и максимальным значениями. В другом варианте этого подхода предлагается сохранять не реальную среднюю протяженность внутри бакета, а протяженность, которая сокращает уровень ошибки общей аппроксимации при запросах по диапазонам значений, принимая во внимание распространенность конкретных диапазонов внутри каждого бакета. Имеется несколько исследований, показывающих превосходство каждого из общих методов над другим; это свидетельствует о том, что абсолютного победителя может и не существовать.
Два
упомянутых основных подхода расширены
и на случай многомерных бакетов с
поддержкой в бакете минимального и
максимального значений каждого измерения.
При использовании предположения о
непрерывности значений больше ничего
и не требуется, но при использовании
предположения о равномерности промежутков
возникает проблема: существование каких
(многомерных) значений предполагается
в бакете? Если
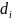 - это число различных значений в атрибуте
, присутствующих в бакете, и
- это число различных значений в атрибуте
, присутствующих в бакете, и
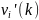 -
-
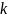 -ое
приближенное число в измерении
(полученное путем применения предположения
о равномерности протяженности по этому
измерению), то разумно предположить,
что в бакете присутствуют все возможные
комбинации
-ое
приближенное число в измерении
(полученное путем применения предположения
о равномерности протяженности по этому
измерению), то разумно предположить,
что в бакете присутствуют все возможные
комбинации
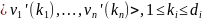 .
(2.26)
.
(2.26)
2.2.4 Анализ бинарных данных
По сути это задача нахождения ассоциированных признаков. Пусть мы имеем таблицу данных магазина по продаже продовольственных продуктов, в которой каждая запись – это покупатель, а поле – это товар, который он купил. Необходимо выявить те товары, которые обычно покупаются вместе.
Данная задача похожа на кластеризацию с той разницей, что кластеризуются не записи, а поля. Для ее решения используется модификация алгоритма слияния.
Допустим,
у нас есть
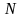 записей (покупателей) и
записей (покупателей) и
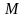 полей (товаров). Обозначим 2 каких-либо
продукта
полей (товаров). Обозначим 2 каких-либо
продукта
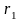 и
и
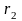 .
Создадим таблицу
.
Создадим таблицу
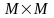 ,
в ней выделим 2 столбца с товарами
и
- их купили соответственно
,
в ней выделим 2 столбца с товарами
и
- их купили соответственно
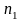 и
и
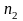 покупателей. Тогда количество покупателей,
купивших продукт
и
совместно будет
покупателей. Тогда количество покупателей,
купивших продукт
и
совместно будет
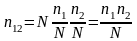 .
(2.27)
.
(2.27)
Зафиксируем
продукт
.
Его купили
человек. Пусть
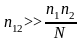 .
Тогда вероятность, что при
испытаний мы получим
.
Тогда вероятность, что при
испытаний мы получим
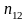 и больше покупок равна
и больше покупок равна
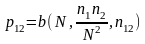 . (2.28)
. (2.28)
Вероятность
того, что товары
и
купит
покупателей равна
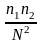 (т.е.
(т.е.
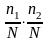 ).
).
С
какой вероятностью при
и при
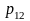 мы получим
и больше покупателей?
мы получим
и больше покупателей?
Чем эта вероятность меньше, тем больше связь между товарами и , т.е. тем более неслучайно такое совпадение. Это мера расстояния между товарами. Тогда - таблица расстояний между товарами.
Для дальнейшего решения используем кластеризацию. Пусть вначале у нас кластеров (по количеству покупателей). Из таблицы выбираем минимальное расстояние и объединяем эту пару товаров в кластер. То же самое проделываем с другими парами товаров. При этом объединение в кластеры производится не всегда.
Для каждого кластера товаров вычисляется вероятность:
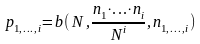 , (2.29)
, (2.29)
которая
является характеристикой данного
кластера (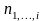 - количество покупателей, купивших все
товары данного кластера). Мы предполагаем
образовать новый кластер. Тогда для
него мы считаем вероятность
- количество покупателей, купивших все
товары данного кластера). Мы предполагаем
образовать новый кластер. Тогда для
него мы считаем вероятность
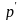 .
Если
.
Если
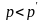 ,
тогда мы присоединяем новый продукт.
,
тогда мы присоединяем новый продукт.
Пусть
есть два кластера с вероятностями
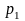 и
и
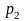 ,
и новая пара товаров принадлежит обоим
кластерам. Мы пытаемся объединить эти
кластеры, высчитываем для нового кластера
вероятность
.
Если
,
и новая пара товаров принадлежит обоим
кластерам. Мы пытаемся объединить эти
кластеры, высчитываем для нового кластера
вероятность
.
Если
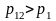 и
и
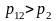 ,
то тогда слияние не производится.
,
то тогда слияние не производится.
Существует
такое понятие как композитный продукт,
например, чипсы, так как есть чипсы с
беконом и есть чипсы с сыром. Если при
попытке присоединить к кластеру чипсов
с беконом мы не получаем уменьшения
характеристики
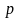 ,
то надо попробовать сначала объединить
в кластер чипсы с беконом и с сыром, а
затем присоединить этот композитный
кластер. Если же при этом снова не
получается уменьшения вероятности
нового кластера по сравнению со старыми,
то из таблицы выбирается продукт из
состава композитного продукта с
наименьшим расстоянием.
,
то надо попробовать сначала объединить
в кластер чипсы с беконом и с сыром, а
затем присоединить этот композитный
кластер. Если же при этом снова не
получается уменьшения вероятности
нового кластера по сравнению со старыми,
то из таблицы выбирается продукт из
состава композитного продукта с
наименьшим расстоянием.
В результате кластеризации мы получим некоторые товары, которые не принадлежат ни одному кластеру.
Также можно задать граничную величину – минимальное число покупателей, для которых такая связь продуктов значима (если число покупателей меньше этой величины, то такая связь неинтересна).
Скорость данного алгоритма зависит от шага вычисления попарных расстояний. Метод квадратичен по количеству полей и линеен по количеству записей.
