Типы символьных данных

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Красноярский государственный аграрный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

dissertatsia_2.docx

Скачиваний:

Добавлен:

01.07.2025

Размер:

695.84 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 185 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Типы символьных данных

Предположим, у нас есть набор данных, состоящий из медицинских карт лиц, таких, которые могут быть сохранены в медицинской страховой компании. Предположим, что для каждого человека, есть географическая запись, например, область(север, северо-восточный, юго-восточный, и т.д.), город (Бостон, Атланта, и т.д.) так же там может присутствовать запись оказанного вида услуг стоматологических, медицинских, оптических и т.д. Там могут быть демографические переменные, такие как пол, семейное положение, возраст, братья и сестры, количество детей, работодатель. Основные медицинские переменные могут включать вес, частоту пульса, кровяное давление и т.д. Другие переменные будут включать в себя случаи определенных недугов и болезней, так же частота заболеваний, способ лечения и другие связанные переменные. Такой набор данных представлен в таблице 2.1, таблица 2.2 содержит описание переменных

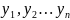. (2.2)

Записи в таблице 2.1 - классические значения в каждой строке содержатся значения переменных 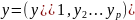для одного человека. Таблица состоит из записей и 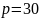переменных. При таком размере, данные могут быть проанализированы с помощью классических методов. Когда размер n велик или очень велик (например, 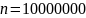, 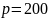), проанализировать такие данные с помощью методов классического анализа весьма проблематично. [7] Любой анализ такой таблицы дает результаты, касающиеся отдельно взятой записи (человека). Например, нужно проанализировать, что происходит с теми, кто обращался за определенным видом медицинских услуг. Таким образом, независимо от размеров набора данных, а не отдельных лиц, можно выделить интересующую категорию людей по определенным критериям. Например, можно выделить группу женщин старше 20 лет, которые пользовались услугами стоматолога, и работать с этим набором данных, как группой людей, а не с каждым человеком отдельно. В этом случае вес женщин будет списком значений 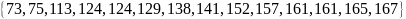, вместо списка данные могут быть представлены в виде интервала 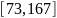. Так же вес может быть представлен в виде гистограмм 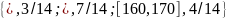, то есть, 7/14 или 50% весят от 110 до 160 кг,

3/14 или 21,4% весят меньше, чем 110 килограмм, и 2/7 или 28,6% весят 160 кг или больше. Переменная вес для данной категории теперь имеет значение, которое представляет собой список, или интервал, или гистограмму, соответственно; и таким образом, представляет собой пример символьных данных.

Таблица 2.1 Классические данные

i	Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8	Y9	Y10	Y11	Y12	Y13	Y14	Y15
1	Красноярск	Т	24	M	Х	2	2	0	165	68	120	79	183	83	86
2	Москва	Т	56	M	Ж	1	2	2	186	84	130	90	164	64	60
3	Омск	Д	48	M	Ж	1	3	2	175	73	126	82	229	109	122
4	Красноярск	Т	47	Ж	Ж	0	1	1	141	78	121	86	239	69	74
5	Омск	Д	79	Ж	Ж	0	3	4	152	84	150	88	187	67	64
6	Минусинск	Т	12	Ж	Х	2	1	0	73	69	126	85	109	98	107
7	Москва	Т	67	Ж	Ж	1	6	0	166	81	134	89	190	90	96
8	Омск	O	73	Ж	Ж	0	2	4	164	77	121	81	181	81	84
9	Красноярск	Д	29	M	Ж	2	0	2	227	62	124	81	214	94	101
10	Красноярск	Д	44	M	Ж	1	3	3	216	71	125	79	218	98	107
11	Москва	Д	54	M	Х	1	5	0	213	57	118	88	189	69	66
12	Кемерово	Т	12	Ж	Х	2	2	0	75	69	115	81	153	54	45
13	Омск	Т	73	Ж	Ж	0	3	1	152	58	123	82	188	87	93
14	Омск	Д	48	M	Ж	0	2	4	206	73	113	72	264	72	62
15	Кемерово	O	79	Ж	Ж	0	3	3	153	72	106	78	118	40	35

Продолжение таблицы 2.1

16	Кемерово	Д	20	M	Х	2	0	1	268	79	123	80	205	85	89
17	Новосибирск	Д	20	Ж	Х	2	4	0	157	75	116	87	180	60	52
18	Москва	Д	17	M	Х	2	2	0	161	69	114	78	169	49	39
19	Москва	Д	31	M	Ж	1	3	2	183	81	118	84	185	66	62
20	Москва	Т	83	M	Ж	0	3	1	128	80	108	80	224	48	65
21	Москва	Т	20	M	Х	1	3	0	182	68	114	76	150	51	40
22	Москва	Т	85	Ж	Ж	0	3	2	161	73	122	76	185	83	89
23	Москва	Д	66	Ж	Х	0	4	3	166	66	126	87	218	98	108
24	Москва	Т	6	M	Х	2	1	0	35	72	114	76	136	52	28
25	Новосибирск	Т	24	M	Ж	2	1	1	177	81	111	82	149	51	39
26	Красноярск	Д	76	M	Ж	0	5	2	192	77	115	73	173	53	44
27	Кемерово	O	57	M	Х	1	3	2	159	72	114	75	234	131	157
28	Омск	Т	11	Ж	Х	2	2	0	73	62	118	80	96	56	43
29	Красноярск	Т	27	Ж	Ж	2	2	1	124	70	114	72	167	67	63
30	Омск	Д	43	Ж	M	2	4	4	148	66	135	97	172	52	43
31	Омск	Т	53	Ж	Х	1	0	3	165	65	135	96	236	134	161
32	Москва	Т	14	M	Х	2	1	0	132	66	125	87	149	51	39
33	Зеленогорск	Д	29	Ж	Ж	1	0	1	153	70	133	92	217	97	106
34	Сосновоборск	Т	84	M	Ж	0	4	1	239	85	114	75	229	126	150
35	Москва	Т	52	M	Ж	0	4	1	206	63	125	86	236	134	161
36	Железногорск	O	86	M	Ж	0	3	3	184	72	114	72	152	53	42
37	Петербург	Т	23	Ж	Х	2	1	0	138	71	125	85	197	96	105
38	Иркутск	Т	51	M	Ж	2	2	2	172	81	119	78	172	73	71
39	Иркутск	Т	70	M	Ж	1	6	3	183	75	114	74	151	52	42
40	Петербург	Т	65	M	Ж	0	4	2	191	84	120	80	175	75	75
41	Кемерово	Т	82	M	Ж	0	3	4	201	79	123	84	188	87	93
42	Петербург	Т	60	M	Х	0	4	0	175	74	117	76	163	63	58
43	Москва	Т	48	M	Ж	1	4	1	187	88	132	98	182	82	86

Окончание таблицы 2.1

44	Иркутск	Т	29	M	Ж	1	1	1	166	59	122	82	178	78	79
45	Ижевск	Т	21	Ж	Ж	2	2	1	124	72	119	79	169	70	67
46	Краснодар	Т	81	Ж	Ж	0	5	3	161	79	128	89	210	109	124
47	Владивосток	Д	70	Ж	Ж	0	3	2	178	72	119	78	230	110	124
48	Курган	Т	27	Ж	Ж	2	0	0	113	77	121	80	179	79	80
49	Норильск	Т	56	Ж	Ж	2	4	1	129	76	119	81	172	72	71
50	Иркутск	Т	64	M	Х	1	2	0	194	81	128	89	210	109	124
51	Иркутск	Т	87	Ж	Ж	0	5	2	157	88	128	88	171	71	70

Таблица 2.1 Классические данные

i	Y16	Y17	Y18	Y19	Y20	Y21	Y22	Y23	Y24	Y25	Y26	Y27	Y28	Y29	Y30
1	2,21	88	92	16	1,4	12	21	69	5,2	14,2	43,6	2,32	Н	Н	0
2	2,55	69	101	16	0,8	20	22	7	4,6	13,5	39,9	2,44	Н	Н	1
3	2,1	114	80	17	1,4	13	24	7,7	4,9	14,1	44,2	2,73	Д	Н	1
4	3,45	44	90	15	1,1	14	20	6,7	4,6	13,9	40,7	2,17	Д	0	0
5	2,79	72	103	18	0,9	20	27	7,3	4,8	11,6	36,1	3,05	Н	0	0
6	1,11	105	108	14	0,8	18	17	6,2	4,3	12,2	36	1,79	Н	0	0
7	2,12	95	91	17	1	17	24	7,2	4,6	13,4	42,3	2,65	Д	6	0
8	2,24	86	112	19	0,9	22	29	8	4	14,9	43,6	3,32	Н	0	0
9	2,28	99	89	18	1	18	27	7,8	4,7	15	43,4	3,13	Н	0	0
10	2,23	103	83	18	1	18	27	7,8	4,5	12,4	37,1	3,12	Д	Н	2
11	2,75	74	100	28	0,3	90	53	11,5	4,3	14,8	42,6	6,32	Н	Н	0
12	2,83	58	119	20	1	19	31	8,3	4,4	14,3	40,7	3,59	Н	0	0
13	2,15	93	69	16	1,2	13	21	6,9	4,6	12,9	37,1	2,35	Н	0	0
14	3,69	49	91	14	1,2	11	16	6,1	5	12,9	40,5	1,67	Н	Н	0
15	2,95	23	82	19	0,9	20	30	8,1	4,1	13,6	43,3	3,4	Н	0	0

Продолжение таблицы 2.1

16	2,4	90	71	19	1,3	14	28	7,9	4,2	13,5	39,4	3,21	Н	Н	0
17	3,01	65	101	17	1	16	23	7,2	5,1	13	40,8	2,61	Н	0	0
18	3,45	54	96	17	1	16	23	7,2	4,2	13,1	40,7	2,61	Н	Н	0
19	2,82	71	146	18	0,7	24	28	7,8	4,8	13,2	38,2	3,14	Н	Н	0
20	4,66	38	111	15	1	14	18	6,4	4,7	13,6	41,7	1,94	Д	Н	3
21	2,94	55	58	13	1,2	11	14	5,8	4	13,7	40,7	1,43	Н	Н	0
22	2,19	90	96	8	0,9	10	17	3,9	4,2	13,1	36,8	7,19	Н	0	0
23	2,22	103	85	18	1,4	13	26	7,6	4,2	13,4	38	2,98	Н	4	0
24	2,6	41	96	16	1,2	13	20	6,8	4,5	15,4	45,2	2,25	Н	Н	0
25	2,96	55	72	19	0,8	24	30	8,2	3,8	14,6	45,4	3,48	Н	Н	0
26	3,27	58	97	17	1,3	13	23	7,2	4,6	12,4	37,1	2,6	Н	Н	0
27	1,78	139	88	17	0,8	22	24	7,2	5	13	37,5	2,65	Н	Н	0
28	1,71	56	136	20	0,8	25	31	7,4	4,6	13,6	41	3,59	Н	0	0
29	2,49	72	104	13	0,7	20	15	5,9	4,7	13,7	41,4	1,53	Н	0	0
30	3,31	57	82	17	0,8	21	25	8,3	4,2	11,7	34	2,83	Д	3	0
31	1,76	141	102	9	1	9	4	7	4,6	11,2	33,9	2,18	Н	1	0
32	2,96	54	120	20	1,1	18	32	8,4	5,3	12,1	38,7	3,67	Н	Н	0
33	2,23	102	99	25	1,1	23	45	10,3	4,6	14,3	41,4	5,29	Н	0	0
34	1,81	134	113	9	1,1	8	4	4,3	4,8	12,3	37,6	2,43	Д	Н	5
35	1,77	14	114	16	1,2	13	22	4,4	4,4	12,9	37	0,15	Н	Н	0
36	2,88	57	92	18	1,2	15	27	6,6	4,2	15,7	49,9	3,11	Н	Н	0
37	2,05	102	70	20	1,4	15	33	8,6	4,1	14,4	40,7	3,78	Н	0	0
38	2,38	77	105	17	1,3	13	23	7,2	4,8	13,5	39,3	2,6	Н	Н	0
39	2,9	56	79	14	0,7	21	17	6,3	5,2	12,3	36,5	1,86	Д	Н	2
40	2,34	80	139	21	1,3	16	34	8,8	4,5	14,6	43,8	3,97	Н	Н	0

Окончание таблицы 2.1

41	2,15	93	111	18	0,8	21	26	7,5	4,6	14,5	44,6	2,91	Н	Н	0
42	2,58	68	112	12	1,2	9	10	5,2	4,7	13,4	38,7	0,91	Н	Н	0
43	2,23	87	95	18	0,8	23	27	7,8	4,3	12,4	37,3	3,13	Н	Н	0
44	2,29	83	77	22	1,5	15	38	9,3	4,3	13,5	38,9	4,43	Н	Н	0
45	2,43	74	103	14	1	14	15	6	4,9	13,5	43,1	1,6	Н	0	0
46	1,93	115	86	15	0,6	23	19	7,8	4,5	11,3	32,9	2,06	Д	3	0
47	2,09	115	87	12	1,2	10	10	5,3	4,4	12,5	39,1	8,88	Д	1	1
48	2,27	84	101	6	1	6	8	3,1	4,2	14,6	40,9	2,99	Н	0	0
49	2,38	77	99	14	1,4	10	16	6,1	4,7	13,9	40,3	1,69	Д	0	4
50	1,93	115	88	19	1,1	17	28	7,9	5	15,3	49,1	3,23	Н	Н	0
51	2,4	76	87	19	1	19	28	7,9	4,6	13,9	44,4	7,14	Н	0	0

Таблица 2.2 Названия переменных

Yi	Описание
Y1	Город
Y2	Тип услуг: Дантист(Д), Терапевт(Т), Окулист(О)
Y3	Возраст (в годах): > 0
Y4	Пол: Мужской(M), Женский(Ж)
Y5	Семейное положение: Холост (Х), Женат/Замужем (Ж)
Y6	Количество родителей: 0, 1, 2
Y7	Количество братьев: 0, 1,...
Y8	Количество детей: 0, 1,...
Y9	Вес в килограммах: > 0
Y10	Пульс: > 0
Y11	Кровянное давление(нижнее): > 0

Окончание таблицы 2.2

Y12	Кровяное давление(верхнее): > 0
Y13	Холестерин: > 0
Y14	HDL Уровень холестерина: > 0
Y15	LDL Уровень холестерина: > 0
Y16	Отношение = Холестерин / ЛПВП Уровень: > 0
Y17	Уровень триглицеридов: > 0
Y18	Уровень глюкозы: > 0
Y19	Показатель карбамида: > 0
Y20	Уровень креатина: > 0
Y21	Отношение = Карбамид /креатин: > 0
Y22	ALT Уровень: > 0
Y23	Показатель лейкоцитов: > 0
Y24	Показатель эритроцитов: > 0
Y25	Гемоглобин: > 0
Y26	Гематокрит: > 0
Y27	Щитовидная железа ТТГ: > 0
Y28	Выявлен рак: Да (Д), Нет (Н)
Y29	Рак молочной железы # лечение: 0, 1,..., нет (Н)
Y30	Рак легких # Лечение: 0, 1, ...

Таблица 2.1 содержит три типа медицинских услуг Y2 = {дантист, терапевт, окулист} и два пола Y4 = {мужчины, женщины}, что дает в общей сложности 3 × 2 = 6 возможных категорий. В таблице 2.3 приводятся агрегированные данные в соответствии этим категориям для переменных

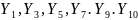(2.3)

Таблица 2.3 Символьные данные

Тип услуг x Пол	Города
дантист женщины	{Новосибирск, Москва, Омск, Зеленогорск, Владивосток}	5
дантист мужчины	{Красноярск, Москва, Кемерово, Омск}	8
окулист женщины	{Омск, Кемерово}	4
окулист мужчины	{Железногорск, Кемерово}	3
терапевт мужчины	{Москва, Новосибирск, Сосновоборск, Иркутск, Петербург, Кемерово, Красноярск}	15
терапевт женщины	{Ижевск, Норильск, Курган, Краснодар, Иркутск, Петербург, Красноярск, Минусинск, Москва, Кемерово, Омск}	16

Категориальная переменная [5] является одним значением, содержащим имена; также ее называют качественной переменной. Количественная переменная содержит одно значение которое являются подмножеством вещественной прямой 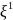. Иногда качественные значения могут быть записаны в виде количественных значений.

В таблице 2.1, переменная Y1 = Город принимает классические категориальные значения, например, в первой записи 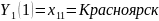, в третьей строке .

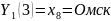Многозначной символической переменной 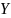называют переменную, которая, принимает одно или несколько значений из списка значений 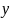. Список возможных значений конечен, и значения могут быть четко заданы в виде категориальных или количественных значений[23].

В таблице 2.3 содержатся обобщенные данные по типам оказанных услуг и половой принадлежности 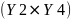. Значения переменной Y1 = Город для категории мужчин, которые обращались к дантисту

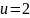
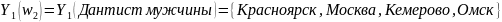
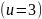
То есть это мужчины, которые обращались к дантисту проживающие в одном из этих городов. Так же определить категорию женщин, которые обращались к окулисту . (2.5)

Если рассмотреть переменную Y5= семейное положение для женщин обращавшихся за помощью к окулисту и мужчин обращавшихся к дантисту увидим следующее:

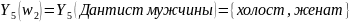(2.6)

. (2.7)

Переменная Y6 = Количество родителей, является количественной многозначной переменной. 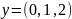определяет принимаемые значения. Мы видим в таблице 2.2, что для мужчин, обращавшихся к стоматологу

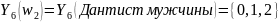(2.8)

Интервально-значной символической величиной называют ту, которая принимает значения в интервале[25]

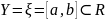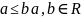, где . (2.9)

Интервал может быть открытым или закрытым то есть 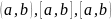или .

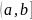Если интервалы возникают в результате агрегирования классических данных, то символические значения 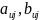для переменной в категории задаются мы получим 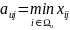, , 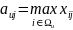где 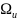- множество значений , составляющих категорию [17].

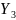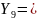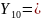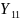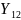В символьной таблице 2.4 переменные = Возраст, Вес, Пульс, = систолическое давление, = диастолическое давление – являются интервально-значными переменными.

Например возраст для

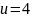
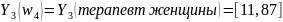(2.10)

Пусть случайная переменная Y принимает значения над областью . Значение называется модальным, если оно имеет следующую форму

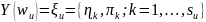(2.11)

для группы u, где 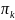неотрицательное значение, связанное с 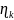и где 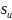число значений в . - может быть конечным или бесконечным числом; оно может быть категориальным или количественным значениями.

Значения 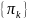как правило веса, вероятности, относительные частоты и т.п., соответствующие компоненту .

компоненты могут быть категориальным значением, или подмножеством вещественной прямой 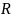, функцией распределения, гистограммой, моделью, или стохастической структурой, связанной с случайной величиной .

Пусть 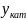область возможных значений для многозначной случайной величины

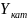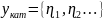, . (2.12)

Тогда, модальная многозначная переменная, принимает значения, подмножества неотрицательной величины, прикрепленной к каждому значению в этой подгруппе. То есть, конкретное наблюдение, для категории , принимает форму:[46]

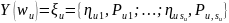(2.13)

где 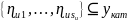и где результат

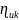
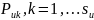и 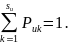(2.14)

Данные символьной таблицы 2.6 является еще одним форматом для данных, полученных из таблицы 2.1. Рассмотрим случайную величину 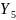= Семейное положение. Мы видим, что для категории мужчин обращавшихся к дантисту

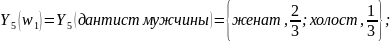(2.15)

То есть доля женатых мужчин, обращавшихся к дантисту, составляет 2/3, а доля не женатых составляет 1/3. Для женщин, обращавшихся к терапевту( ) имеем:

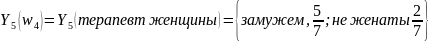(2.16)

Это значит что, доля замужних женщин, обращавшихся за помощью к терапевту, составляет 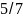а не замужних 2/7.

Пусть количественная величина, которая может принимать значения от конечного числа непересекающихся интервалов 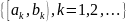, где 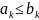. Тогда значение для группы будет называться гистограммой интервал-значной переменной и будет иметь следующую форму[19]:

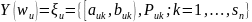(2.17)

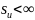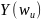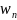где - конечное число интервалов для и 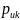– вес для конкретного подинтервала

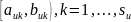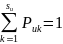и . (2.19)

Интервалы могут быть открытыми или закрытыми с обоих концов.

Рассмотрим данные о состоянии таблицы 2.6. Эти данные получились в результате агрегации данных таблицы 2.1. В отличие от агрегации, представленной в таблице 2.4, в которой содержатся интервальные данные, эта агрегация привела значения к модальным. Случайные величины = возраст, 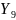= вес и 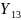= холестерин - являются гистограммами интервал-значных переменных. Рассмотрим . Пациенты, уровень холестерина которых равен или больше 240, подвержены риску сердечнососудистых заболеваний, те у которых уровень холестерина попадает в интервал 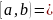почти подвержены риску, те, у которых холестерин меньше 200 полностью здоровы. Поэтому, распределения гистограмм значений холестерина именно этих трех интервалов представляет интерес.

Проанализируем мужчин обращавшихся к дантисту ( )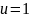

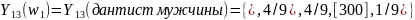(2.20)

Видно, что на гране риска заболеть сердечнососудистыми заболеваниями находятся 4/9, 1/9 подвержена риск, 4/9 полностью здоровы.

Тип услуг X пол	Возраст	Семейное положение	родители	вес	пульс	Систолическое давление	Диастолическое давление	холестерин
	Y3	Y5	Y6	Y9	Y10	Y11	Y12	Y13
дантист мужчины	[17, 76]	{Ж, Х}	{0,1,2}	[161, 268]	[57, 81]	[113, 126]	[72, 88]	[179, 264]
дантист женщины	[20, 70]	{Ж, Х}	{0,1,2}	[148, 178]	[66, 84]	[116, 150]	[78, 97]	[172, 230]
терапевт мужчины	[6, 84]	{Ж, Х}	{0,1,2}	[35, 239]	[59, 88]	[108, 132]	[74, 98]	[109, 236]
терапевт женщины	[11, 87]	{Ж, Х}	{0,1,2}	[73, 166]	[58, 88]	[114, 135]	[72, 96]	[96, 239]
окулист мужчины	[57, 86]	{Ж, Х}	{0, 1}	[159, 184]	[72, 72]	[114, 114]	[72, 78]	[152, 234]
окулист женщины	[73, 79]	{Ж}	{0}	[153, 164]	[72, 77]	[106, 121]	[78, 81]	[118, 181]

Таблица 2.4 Символьные данные

Таблица 2.5 Символьные модальные переменные, агрегированные из таблицы 2.1

Тип услуг X пол	Возраст( )	Семейное положение( )	родители( )	вес( )	холестерин( )
дантист мужчины	{[0, 40), 4/9 [40, 99], 4/9}	{Ж, 2/3 Х, 1/3}	{0, 2/9 1, 4/9 2, 1/3}	{[150, 200), 4/9 [200, 275], 5/9}	{[<200), 4/9 [200, 300), 4/9, [300], 1/9]}
дантист женщины	{[0, 40), 1/3 [40, 99], 2/3}	{Ж, 1/2 Х 1/2}	{0, 1/2 1, 1/16 2, 1/3}	{[140, 160), 2/3 [160, 180], 1/3}	{[<200), 1/2 [200, 240), 1/2}
терапевт мужчины	{[0, 20), 1/6 [20, 40), 2/89 [40, 60], 2/9 [60, 99], 7/18}	{Х, 11/18 Х 7/18}	{0, 1/3 1, 1/3 2, 1/3}	{[0, 120), 1/9 [120, 180), 7/8 [180, 240], 1/2}	{[<200), 7/9 [200, 240), 2/9}
терапевт женщины	{[0, 20), 1/7 [20,40), 2/7 [(40, 60), 3/14 [60, 99], 5/14}	{Х, 5/7 Х, 2/7} {0, 5/14 1, 1/7 2, 1/2}	{[50, 110), 1/7 [110, 140), 5/14 [140, 170] 1/2}	{[<200), 11/14 [200, 240), 3/14}
окулист мужчины	{[40, 60), 1/2 [60, 99], 1/2}	{Ж, 1/2 Х 1/2}	{0, 1/2 1, 1/2}	{[140, 160), 1/2 [160, 200], 1/2}	{[<200), 1/2 [200, 240), 1/2}
окулист женщины	{[60, 99]} {Ж} {0}	{[140, 160), 1/2 [160, 180] 1/4}	{[<200)}

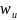
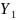
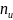
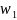
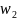
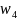
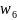
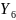<<< < Предыдущая 1 2 3 45 / 185 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.04.2015273.41 Кб27Course I Units 6-10.doc
#
10.04.201521.16 Кб10crosswoвrd.docx
#
10.04.2015215.55 Кб42d0adfc631d3cf377a215057e310e1695.doc
#
01.05.202576.83 Кб0Diplomatia.docx
#
01.04.202546.98 Кб0dip_rabota_polozh_-_kopia.docx
#
01.07.2025695.84 Кб0dissertatsia_2.docx
#
10.04.201530.28 Кб49dlya_devochek.docx
#
10.04.201530.37 Кб49dlya_malchikov.docx
#
19.09.2019105.47 Кб8dnevnik_proizvodstvennoy_praktiki.doc
#
15.03.2016136.19 Кб18dnevnik_prp.doc
#
01.05.202559.66 Кб0Dnevnik_terapia (1).docx