Глава 2. Символьный анализ данных

Как правило, мы анализируем классические данные, в которых каждое значение является единственной точкой в ​​n-мерном пространстве 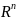. Тем не менее, данные в виде списков, интервалов, гистограмм и т.п. являются примерами символьных данных, введенных Edvin Diday (1987). Символические данные имеют внутреннюю структуру, которой не может существовать в классических данных. К сложно структурированным данным не применима статистическая теория и методы классических данных. Поэтому, разработка новых методов для анализа символьных данных и построения математических основ имеют большую актуальность.

Edwin Diday (1995), Эмильон (1997) и Diday и Эмильон (1996, 1998) описали оригинальную математическую основу символических данных в серии работ. В своих работах, они обозначили, что символическая случайная величина может занимать конечное или счетное множество значений в 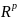. Есть несколько основных типов символьных данных[1]. Многозначные данные, то есть список значений, интервальные данные, более сложный тип модально-значные данные, в которых содержатся вероятности, веса, или другие связанные значения. Хорошим примером модального-значных данных является гистограмма.

Как правило, символьные данные возникают в двух случаях, при сборе и обработке информации. Некоторые собранные данные по своей природе являются символьными, некоторые становятся символьными после обработки. Прежде всего, исходные данные могут быть собраны как списки, интервалы, гистограммы, и т.п. Примером естественно, собранной символической информации являются показания артериального давления, где измерительный прибор на самом деле измеряет диапазон (хотя это значение может быть записано как одно значение). Другой пример символических данных - уровень доходов. Аналитики опроса хорошо знают, что спрашивая человека о его дохода напрямую, обычно получают не точный ответ. Вместо точного ответа можно предоставить несколько диапазонов значений, таких как

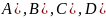(2.1)

Другая важная причина использования символьного анализа состоит в том, что иногда наборы данных слишком велики[1]. С появлением современной информатики крупные наборы данных становятся обычным делом, и проанализировать эти данные очень сложно, а порой не возможно, так как для проведения статистического анализа могут потребоваться большие вычислительные мощности. Чтобы решить эту проблему, была проделана большая работа по разработке более эффективных алгоритмов. Хотя улучшенные алгоритмы решают проблему, они по-прежнему ограничены в полезности. Тем не менее, простым способом решения этой проблемы является агрегирование отдельных данных на группы по некоторым параметрам, это особенно эффективно, когда характеристики групп представляют больший интерес для аналитика. Таким образом, первоначальный набор данных сводится к наборам данных меньшего объема, сохраняя при этом интересные знания.[2]

Регрессия как статистический инструмент для исследования отношений между зависимыми и независимыми переменными, долго был одним из основных методов анализа в области статистики. Регрессия также становилась областью активных исследований в области экономики, психологии, образования, биологических областях и др. Лежандром (1805) и Гауссом (1809) впервые был введен метод наименьших квадратов для регрессии для решения проблемы определения орбит объектов вокруг Солнца на основе астрономических наблюдений.

Адаптация регрессии для символьных данных, особенно интервально-значных данных стала областью активных исследований. Billiard и Diday (2000) разработали способ применения регрессионной модели к интервально-значным данным [13].