
- •Магистерская диссертация
- •230400.68 Информационные системы и технологии
- •230400.68.01 Информационно-управляющие системы
- •Глава 1. Информационно-аналитические технологии анализа данных……………………………………………………………………………...7 1.1 Роль и место информационно-аналитических систем…………7
- •Глава 2. Символьный анализ данных…………………………………..19
- •Глава 3. Применение символьного анализа в информационно аналитических системах......................................................................................57
- •Реферат
- •Введение
- •Глава 1. Информационно-аналитические технологии анализа данных
- •1.1 Роль и место информационно-аналитических систем
- •1.2 Технологии извлечения данных
- •Глава 2. Символьный анализ данных
- •Типы символьных данных
- •2.2 Гистограммы как символическое представление данных
- •2.2.1 Распределение данных
- •2.2.2 Обоснование гистограмм
- •2.2.3 Аппроксимация значений внутри каждого бакета
- •2.2.4 Анализ бинарных данных
- •2.2.5 Построение гистограмм
- •2.2.6 Гистограммы символьных последовательностей
- •2.4 Визуально интерактивные методы анализа данных
- •2.4.1 Теория Доу
- •2.4.2 Волновая теория Эллиотта
- •2.4.3 Метод японских свечей.
- •Глава 3. Применение символьного анализа в информационно аналитических системах
- •3.1.1 Одна зависимая переменная.
- •3.1.2 Многозначные переменная
- •3.1.3 Интервальные переменные
- •3.1.4 Гистограммные переменные
- •3.2 Кластерный анализ
- •3.2.1 Многозначные переменные
- •3.2.2 Интервальные переменные
- •3.3 Кластерный анализ в распознавании изображений
- •Заключение
- •Список использованных источников
- •Приложение а Исходный код программы распознавания изображений
3.2.1 Многозначные переменные
Пусть
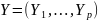 p-мерная
многозначная случайная величина,
принимающая значения
p-мерная
многозначная случайная величина,
принимающая значения
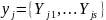 .
Будем считать, что каждый
.
Будем считать, что каждый
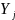 является модально-значным и что все
возможные значения в
является модально-значным и что все
возможные значения в
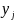 могут произойти. Значение,
следовательно, моно записать в следующем
виде, для каждого
могут произойти. Значение,
следовательно, моно записать в следующем
виде, для каждого

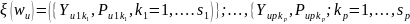 (3.38)
(3.38)
где
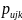 относительная частота
относительная частота
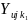 .[6]
Тогда значения
.[6]
Тогда значения
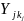 в
которые не встречаются в
в
которые не встречаются в
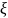 имеют соответствующие значения
имеют соответствующие значения
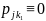 .
Кроме того, для не модальной многозначной
случайной величины, это
.
Кроме того, для не модальной многозначной
случайной величины, это
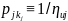 где
где
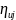 количество значений в
,
которые имеют место.
количество значений в
,
которые имеют место.
Пусть
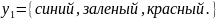 Тогда
Тогда
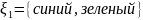 перепишем в виде
перепишем в виде
 ,
аналогичным образом
,
аналогичным образом
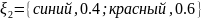 становится
становится

Для
многозначных модальных данных виде
уравнения (3.39), категорические меры
расстояния между любыми двумя наблюдениями
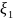 и
и
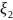 является
является
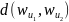 где
где
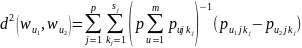 (3.39)
(3.39)
Рассмотрим
следующие значения,
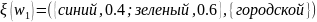

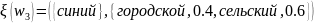 (3.40)
(3.40)
Приведем к формату уравнения относительно частот
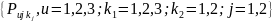 . (3.41)
. (3.41)
Тогда
из уравнения (3.39), квадрат расстояния
между
и
является
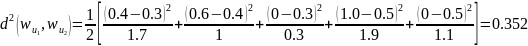
Аналогичным
образом получаем
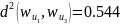
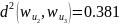
Следовательно, матрица расстояний будет выглядеть следующим образом
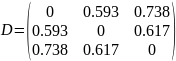 (3.42)
(3.42)
Обратите внимание, D является матрицей Робинсона.
Есть две меры, которые применяются к не модальным многозначным переменным. Они имеют следующий формат
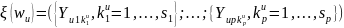 (3.43)
(3.43)
3.2.2 Интервальные переменные
Есть целый ряд несходств и расстояний мер по интервально-значным данным, некоторые из которых имеют сходства с многозначными переменными и некоторые из которых являются уникальными для интервальных данных. Опишем реализацию интервальных данных.
![]() (3.44)
(3.44)
Gowda-Diday несходство мер между двумя интервальными значениями и имеет следующую форму [5]
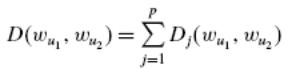 (3.45)
(3.45)
где расстояние
![]() (3.46)
(3.46)
![]() ,
(3.47)
,
(3.47)
где
![]() (3.48)
(3.48)
длинна
всей дистанции на протяжении от
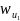 до
до
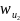 c
c
![]() (3.49)
(3.49)
где
 - длинна пересечения интервалов
- длинна пересечения интервалов
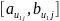 и
и
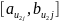
![]() (3.50)
(3.50)
если
интервалы пересекаются, и
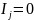 если
нет.
если
нет.
![]() ,
(3.51)
,
(3.51)
где
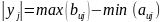 .
.
Компоненты
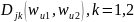 из уравнений (3.46) - (3.47) являются аналогами
компонентов расстояния Gowda-Diday для
многозначных величин, заданных в
определении 3.15. Третий компонент
из уравнений (3.46) - (3.47) являются аналогами
компонентов расстояния Gowda-Diday для
многозначных величин, заданных в
определении 3.15. Третий компонент
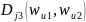 является
мерой взаимного расположения двух
наблюдений.
является
мерой взаимного расположения двух
наблюдений.
3.3 Кластерный анализ в распознавании изображений
Постановка
задачи. Пусть
имеется некоторое изображение
.
Требуется выбрать из базы знаний
изображение
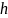 ,
такое что
,
такое что
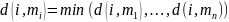 (3.52)
(3.52)
где
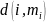 - метрика гистограммы изображения
- количество изображений в базе знаний.
- метрика гистограммы изображения
- количество изображений в базе знаний.
Решение. Для решения задачи, был составлен следующий алгоритм.
Распознавание изображений происходит следующим образом:
Заполняется база знаний.
Строится гистограмма изображения.
По формуле
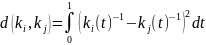 (3.53)
(3.53)
вычисляются
метрики изображений, где
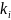 -
значения гистограмм распознаваемого
изображения,
-
значения гистограмм распознаваемого
изображения,
 -
значения гистограмм изображения из
базы знаний. Анализ публикаций показал,
что эта формула максимально эффективна
для решения данной задачи.
-
значения гистограмм изображения из
базы знаний. Анализ публикаций показал,
что эта формула максимально эффективна
для решения данной задачи.
Выбирается изображение с меньшей метрикой
Выводится результат

Рисунок 3.1 Блок схема программы
Программа была реализована на языке программирования C# в среде разработки visual studio 2008. На изображении 3.2 приведен тестовый пример работы программы. Слева расположено исходное изображение (то для которого ищем похожее), справа расположено найденное похожее изображение из базы знаний.
На изображении 3.3 в базу были загружены различные спутниковые снимки местности. Слева эталонное изображение, справа найденное в базе знаний.
Таким образом, данная разработка может использоваться в системе спутникового мониторинга, например для прогнозирования весенних паводков.
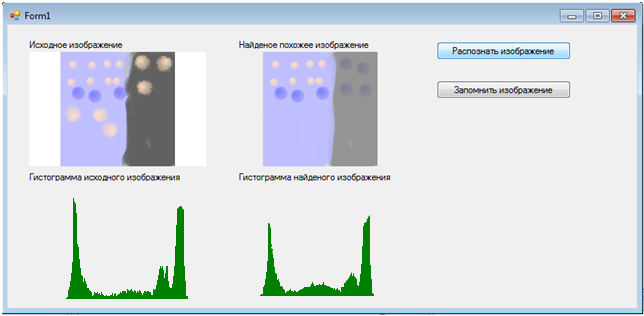
Рисунок 3.2 Интерфейс программы.
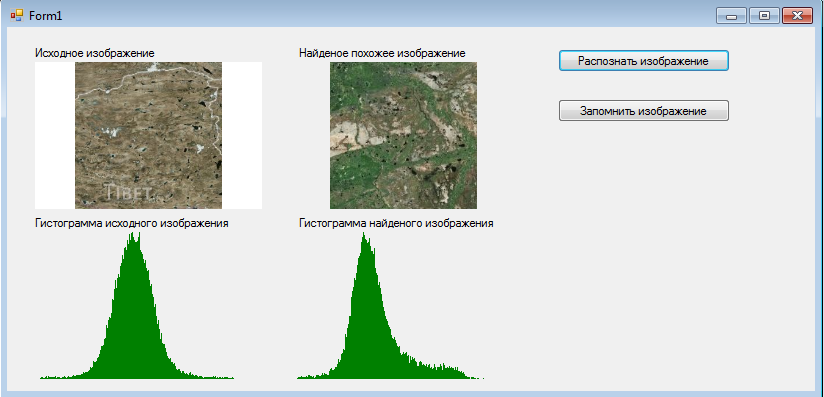
Рисунок 3.3 Пример работы программы
На рисунке 3.2 представлен практический пример работы программы.
