
- •Магистерская диссертация
- •230400.68 Информационные системы и технологии
- •230400.68.01 Информационно-управляющие системы
- •Глава 1. Информационно-аналитические технологии анализа данных……………………………………………………………………………...7 1.1 Роль и место информационно-аналитических систем…………7
- •Глава 2. Символьный анализ данных…………………………………..19
- •Глава 3. Применение символьного анализа в информационно аналитических системах......................................................................................57
- •Реферат
- •Введение
- •Глава 1. Информационно-аналитические технологии анализа данных
- •1.1 Роль и место информационно-аналитических систем
- •1.2 Технологии извлечения данных
- •Глава 2. Символьный анализ данных
- •Типы символьных данных
- •2.2 Гистограммы как символическое представление данных
- •2.2.1 Распределение данных
- •2.2.2 Обоснование гистограмм
- •2.2.3 Аппроксимация значений внутри каждого бакета
- •2.2.4 Анализ бинарных данных
- •2.2.5 Построение гистограмм
- •2.2.6 Гистограммы символьных последовательностей
- •2.4 Визуально интерактивные методы анализа данных
- •2.4.1 Теория Доу
- •2.4.2 Волновая теория Эллиотта
- •2.4.3 Метод японских свечей.
- •Глава 3. Применение символьного анализа в информационно аналитических системах
- •3.1.1 Одна зависимая переменная.
- •3.1.2 Многозначные переменная
- •3.1.3 Интервальные переменные
- •3.1.4 Гистограммные переменные
- •3.2 Кластерный анализ
- •3.2.1 Многозначные переменные
- •3.2.2 Интервальные переменные
- •3.3 Кластерный анализ в распознавании изображений
- •Заключение
- •Список использованных источников
- •Приложение а Исходный код программы распознавания изображений
3.1.3 Интервальные переменные
Для
интервальных значений, зависимая
переменная
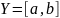 и переменная предиктор
,
где
и переменная предиктор
,
где
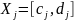 ,
,
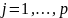 .
Регрессионный анализ будем проводить
с помощью уравнений классической
методологии, но с символическими
переменными для матриц
.
Регрессионный анализ будем проводить
с помощью уравнений классической
методологии, но с символическими
переменными для матриц
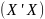 и (
и (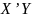 ).
).
Таким образом
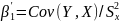 (3.20)
(3.20)
и
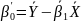 (3.21)
(3.21)
где
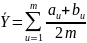 ,
,
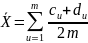
И
где
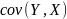 вычисляется по формуле[50]
вычисляется по формуле[50]
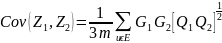 . (3.22)
. (3.22)
Данные таблицы 3.5 приводят интервал-значные переменные для прогнозируемой переменной X = Возраст и двух зависимых случайных величин Y1 = холестерина и Y2 = вес для определенной группы людей. Возрастные группы представлены для лиц, входящих в состав исходного набора данных.
Таблица 3.5 Возраст, уровень холестерина, вес. |
||||
|
X Возраст |
Y1 уровень холестерина |
Y2 вес |
|
|
[20, 30) |
[114, 192] |
[108, 141] |
43 |
|
[30, 40) |
[103, 189] |
[111, 150] |
66 |
|
[40, 50) |
[120, 191] |
[127, 157] |
75 |
|
[50, 60) |
[136, 223] |
[130, 166] |
43 |
|
[60, 70) |
[149, 234] |
[139, 161] |
59 |
|
[70, 80) |
[142, 229] |
[143, 169] |
35 |
|
[80, 90) |
[140, 254] |
[140, 176] |
18 |
Предположим, Y1 = Холестерин единая зависимая переменная, предиктор X= возраст.
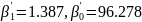 (3.23)
(3.23)
Следовательно
уравнение регрессии примет следующий
вид
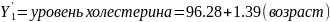 .
.
Предположим,
что мы сейчас берем зависимую переменную
Y2 = Вес, и предположим, мы проводим
взвешенную анализ с весами, пропорциональными
количеству лиц, что были объединены, в
соответствующие классы
.
В этом случае получаем
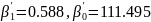 и
и
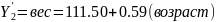 .
.
Альтернатива методологии регрессии. Расчета середины для каждого интервала
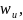
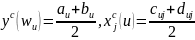 (3.24)
(3.24)
а затем использовать методологию регрессии.
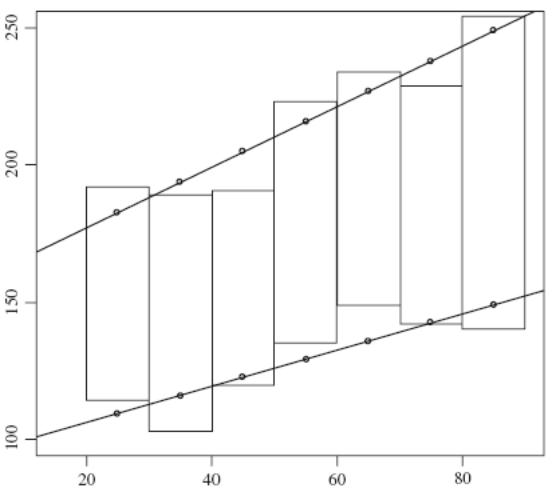
Уровень холестерина
Возраст
Рисунок 3.1 Регрессия
3.1.4 Гистограммные переменные
Понятия, используемые для интервал-значных значений могут быть применены к гистограмм-значным значениям по аналогии с использованием, среднего, дисперсии и ковариационной функции от гистограмм-значных данных. Для простоты, будем считать, что существует единая р = 1 переменная предиктор Х и зависимая переменная является Y. Когда мы рассматривали многозначные переменные, предпологалось, что они могут содержать все возможные значения, хотя некоторые с нулевой вероятностью. Это обобщение не возможно для модальных интервальных-значных (т.е. количественных гистограмм) так как гистограмма подынтервалов не то же самое для всех наблюдений . [20]
 (3.25)
(3.25)
где
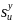 количество гистограмм подинтервалов
для значения Y.
количество гистограмм подинтервалов
для значения Y.
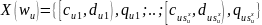 (3.26)
(3.26)
где
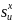 число гистограмм подинтервалов для
наблюдаемых значений X.
число гистограмм подинтервалов для
наблюдаемых значений X.
В
общем
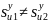 ,
,
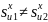 для
для
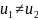 и
и
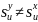 .
Где
.
Где
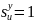 и
и
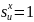 для
для
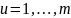 как частный случай интервал-значных
данных.
как частный случай интервал-значных
данных.
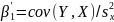 и
,
(3.27)
и
,
(3.27)
где
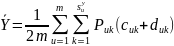 (3.28)
(3.28)
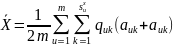 (3.29)
(3.29)
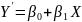 (3.30)
(3.30)
Пример.
Данные таблицы 3.6 представляют
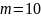 гистограмм-значных переменных, где
зависимой переменной является Y =
гематокрит и переменной предиктором
является X = гемоглобин. Обратите внимание,
что
и
гистограмм-значных переменных, где
зависимой переменной является Y =
гематокрит и переменной предиктором
является X = гемоглобин. Обратите внимание,
что
и
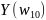 интервал-значные. Мы хотим, чтобы данные
соответствовали модели
интервал-значные. Мы хотим, чтобы данные
соответствовали модели
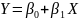 .
Имеем
.
Имеем
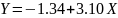 .
подставляя значения X,
имеем следующие значения.
.
подставляя значения X,
имеем следующие значения.
Таблица 3.6 Гистограмные переменные
|
Y |
X |
|
{[33.29, 37.52), 0.6| [37.52, 39.61], 0.4} |
{[11.54, 12.19), 0.4| [12.19, 12.80], 0.6} |
|
{[36.69, 39.11), 0.3| [39.11, 45.12], 0.7} |
{[12.07, 13.32), 0.5| [13.32, 14.17], 0.5} |
|
{[36.69, 42.64), 0.5| [42.64, 48.68], 0.5} |
{[12.38, 14.20), 0.3| [14.20, 16.16], 0.7} |
|
{[36.38, 40.87), 0.4| [40.87, 47.41], 0.6} |
{[12.38, 14.26), 0.5| [14.26, 15.29], 0.5} |
|
{[39.19, 50.86]} |
{[13.58, 14.28), 0.3| [14.28, 16.24], 0.7} |
|
{[39.70, 44.32), 0.4| [44.32, 47.24], 0.6} |
{[13.81, 14.50), 0.4| [14.50, 15.20], 0.6} |
|
{[41.56, 46.65), 0.6| [46.65, 48.81], 0.4} |
{[14.34, 14.81), 0.5| [14.81, 15.55], 0.5} |
|
{[38.40, 42.93), 0.7| [42.93, 45.22], 0.3} |
{[13.27, 14.00), 0.6| [14.00, 14.60], 0.4} |
|
{[28.83, 35.55), 0.5| [35.55, 41.98], 0.5} |
{[9.92, 11.98), 0.4| [11.98, 13.80], 0.6} |
|
{[44.48, 52.53]} |
{[15.37, 15.78), 0.3| [15.78, 16.75], 0.7} |
|
|
|
Если
бы середина значения каждой гистограммы
подинтервале использовались вместо
классических значений, Уравнения (3.28)
- (3.30) даст
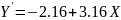 .
.
Как уже говорилось в разделе для интервал-значных переменных, использование только середин подинтервала имеет эффект потери внутренних изменений в пределах наблюдений, в то время как с помощью символической ковариации можно избежать этих потерь.
Для
гематокрита-гемоглобина гистограмм-значных
данных таблицы 6.8, использование в полной
мере символических интервалов дает
значение ковариационной
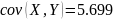 ,
в то время как с метод подинтервальной
середины дает значение
,
в то время как с метод подинтервальной
середины дает значение
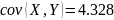 .
Видно что, при использовании средних
точек некоторые вариации данных теряются.
.
Видно что, при использовании средних
точек некоторые вариации данных теряются.
