3.1.2 Многозначные переменная

Предположим, что зависимая переменная может принимать любое значение из списка значений 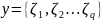. Запишем это для наблюдения

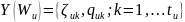(3.14)

где для наблюдения результат 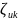относительно частоты 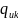, и где 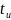количество значений в . Пусть 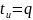для всех 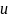, то есть те 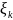которые не входят в будут иметь частоту 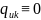.[23]

Таким же образом, переменная - предиктор 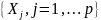. Обозначим зависимую переменную 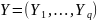, 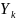представляет возможный исход относительно частоты 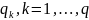. Обозначенную модель регрессии между переменными Y и X можно рассматривать как объявленную ранее модель классической множественной регрессии.

Таким образом, методы многомерных моделей множественной регрессии легко распространяются на символические многозначные переменные [18]. Рассмотрим пример регрессии для модальной многозначной переменной.

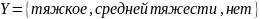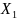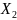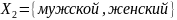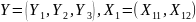Было проведено исследование, чтобы изучить взаимосвязь, между полом(X1) и возрастом(X2) от тяжести преступлений Y. Зависимая переменная Y принимает следующие значения . Возраст принимает значения и пол принимет значения . Эти случайные величины были закодированы, соответственно, и . Данные представлены в таблице ниже. Например для группы1 мы имеем следующие данные

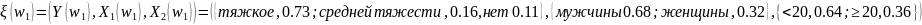(3.15)

То есть в группе 1, 64% были моложе 20 лет, 36% были 20 лет и старше, 68% были мужчинами и 32% составляли женщины, 73% из них были осуждены за тяжкие преступления, 16% за преступления средней тяжести, и 11% из них не были осуждены.

Таблица 3.3 Демография преступности

	тяжкие	Y2 средней тяжести	Y3 нет	X11 мужчины	X12 женщины	X21 <20	X21
группа1	0.73	0.16	0.11	0.68	0.32	0.64	0.36
группа2	0.40	0.20	0.40	0.70	0.30	0.80	0.20
группа3	0.20	0.20	0.60	0.50	0.50	0.50	0.50
группа4	0.10	0.20	0.70	0.60	0.40	0.40	0.60
группа5	0.20	0.40	0.40	0.35	0.65	0.55	0.45
группа6	0.48	0.32	0.20	0.53	0.47	0.62	0.38
группа7	0.14	0.65	0.21	0.40	0.60	0.33	0.67
группа8	0.37	0.37	0.26	0.51	0.49	0.42	0.58
группа9	0.47	0.32	0.21	0.59	0.41	0.66	0.34
группа10	0.18	0.15	0.77	0.37	0.63	0.22	0.78
группа11	0.35	0.35	0.30	0.41	0.59	0.44	0.56
группа12	0.18	0.57	0.25	0.39	0.61	0.45	0.55
группа13	0.74	0.16	0.10	0.70	0.30	0.63	0.37
группа14	0.33	0.45	0.22	0.37	0.64	0.29	0.71
группа15	0.35	0.39	0.26	0.50	0.50	0.44	0.56

Многофакторная модель регрессии для 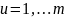будет выглядеть следующим образом

,

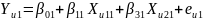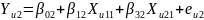(3.16)

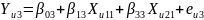
Где для зависимая переменная записывается как 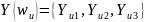. Обратите внимание, что так как X1 и X2 переменные типа кодированной переменной, одна из 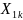и одна из переменных 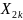опущенf в регрессионной модели. Тем не менее, все кодированные Y переменные сохраняются, поэтому в данном случае есть q = 3 уравнения, по одному для каждого значения переменной Y. Тогда из уравнения (3.16), мы можем определить параметры по 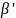, чтобы представить модель регрессии в виде

, где

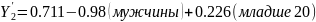(3.17)

Подставляя значения X в уравнение 3.18 расcчитаем Y. Например, для первой группы.

,

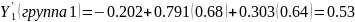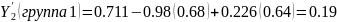, (3.18)

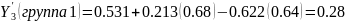
Прогноз преступлений группы1 характеристиками пола и возраста:

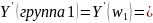
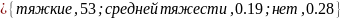(3.19)

То есть 53% вероятно будут осуждены за тяжкие преступления, 19% преступления средней тяжести, и 28% не будут осуждены. Прогнозируемые показатели преступности для каждой группы представлены в таблице ниже.

Таблица 3.4 Прогноз преступности.

w_u	Y1 тяжкое	Y2 средней тяжести	Y3 нет	R1	R2	R3
группа1	0.53	0.19	0.28	0.20	-0.03	-0.17
группа2	0.59	0.21	0.18	-0.19	-0.01	0.22
группа3	0.34	0.33	0.33	-0.14	-0.13	0.27
группа4	0.39	0.21	0.41	-0.29	-0.01	0.29
группа5	0.24	0.49	0.26	-0.04	-0.09	0.14
группа6	0.41	0.33	0.26	0.08	-0.01	-0.06
группа7	0.21	0.39	0.41	-0.07	0.26	-0.20
группа8	0.33	0.31	0.38	0.04	0.06	-0.12
группа9	0.46	0.28	0.25	0.01	0.04	-0.04
группа10	0.16	0.40	0.47	0.02	-0.25	0.30
группа11	0.26	0.41	0.34	0.09	-0.06	-0.04
группа12	0.24	0.43	0.33	-0.06	0.14	-0.08
группа13	0.54	0.17	0.29	0.20	-0.01	-0.19
группа14	0.18	0.41	0.43	0.15	0.04	-0.21
группа15	0.33	0.32	0.36	0.02	0.07	-0.10