3.1.1 Одна зависимая переменная.
Многозначная случайная величина является одним значением, которое содержит список категориальных значений, то есть, каждое наблюдение принимает значение
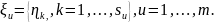(3.7)
Модальное многозначная случайная величина, является одной величиной, значение, которой имеет вид
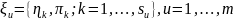(3.8)
Очевидно,
что не модальная многозначная переменная
в уравнении (3.7) является частным случаем
модальной многозначной переменной, где
каждое значение
в этом списке имеет одинаковую вероятность.
В дальнейшем мы будем принимать
относительно частоты
.
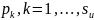Для
ясности давайте обозначим независимыми
предикторами переменные
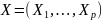со значениями
,
где
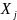имеет вид
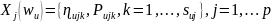(3.9)
на
наблюдении
.
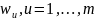Пусть возможные значения
в
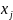будут
.
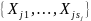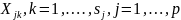– тип переменной индикатора принимающая
значения частоты
,
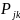соответственно. Мы берем
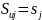для
всех наблюдений
и установим наблюдаемую
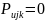для таких значений что
.
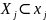Пусть зависимая переменная обозначается
Y
и принимает значения в пространстве
.
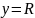будет
принимать только количественное или
качественное значение.[24]
Регрессионный
анализ для этих многозначных переменных
выполняется, так же как и в классической
множественной регрессии из предыдущей
главы, обычным способом.
принимает
значения
символьных данных[9]. Заметим, что, так
как
представляет собой тип переменной-индикатора,
только
включены в модели, чтобы позволить
инверсию матрицы
.
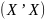Таблица 3.1 – Расход топлива
|
Регион |
Y = Расход |
X = Тип топлива
|
|
Регион1 |
28.1 |
{газ, 0.83 масло, 0.03 электричество, 0.14} |
|
Регион2 |
23.4 |
{газ, 0.69 масло, 0.13 электричество, 0.12 другое, 0.06} |
|
Регион3 |
33.2 |
{масло, 0.40 электричество, 0.15 другое, 0.45} |
|
Регион4 |
25.1 |
{газ, 0.61 масло, 0.07 электричество, 0.16 другое, 0.16} |
|
Регион5 |
21.7 |
{газ, 0.67 масло, 0.15 электричество, 0.18} |
|
Регион6 |
32.5 |
{газ, 0.40 электричество, 0.45 другое, 0.15} |
|
Регион7 |
26.6 |
{газ, 0.83 масло, 0.01 электричество, 0.09 |
|
Регион8 |
19.9 |
{газ, 0.66 масло, 0.15 электричество, 0.19} |
|
Регион9 |
28.4 |
{газ, 0.86 электричество, 0.09 другое, 0.05} |
|
Регион10 |
25.5 |
{газ, 0.77 электричество, 0.23} |
В
таблице 3.1 приведены средние затраты
на топливо(Y
в кодированных долларах), потраченные
в год и типы используемого топлива X,
для отопления в нескольких различных
регионах страны. Полный набор возможных
значений
,
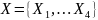то есть
.
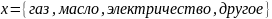(3.10)
Таким
образом, мы видим, например, что в регионе1
,
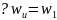83% используется газ, 3% масло и 14% используют
электричество для отопления своих
домов, в среднем расходов
.
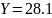Составим уравнение классической регрессии:
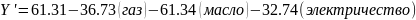(3.11)
отметим,
что хотя переменная
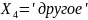не входит непосредственно в уравнение,
она косвенно присутствует, когда
соответствующие значения для
,
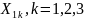вводятся в модель.
Подставляя
наблюдаемые значения X в полученное
уравнение, прогнозируем регулярные
расходы,
и соответствующие остатки R = Y –
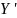получаются. Например, для региона 1(
),
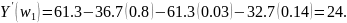(3.12)
Вычислим остаток:
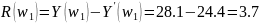(3.13)
Прогнозируемые значения и остатки для всех регионов приведены в таблице 3.2.
Таблица 3.2 – Расходы топлива, параметры регрессии
|
Регион |
Y |
газ |
масло |
электричество |
другое |
Y' |
R |
|
регион1 |
28.1 |
0.83 |
0.03 |
0.14 |
0.00 |
24.40 |
3.70 |
|
регион2 |
23.4 |
0.69 |
0.13 |
0.12 |
0.06 |
24.07 |
0.67 |
|
регион3 |
33.2 |
0.00 |
0.40 |
0.15 |
0.45 |
31.87 |
1.33 |
|
регион4 |
25.1 |
0.61 |
0.07 |
0.16 |
0.16 |
29.37 |
4.27 |
|
регион5 |
21.7 |
0.67 |
0.15 |
0.18 |
0.00 |
21.61 |
0.09 |
|
регион6 |
32.5 |
0.40 |
0.00 |
0.45 |
0.15 |
31.89 |
0.61 |
|
регион7 |
26.6 |
0.83 |
0.01 |
0.09 |
0.07 |
27.26 |
0.66 |
|
регион8 |
19.9 |
0.66 |
0.15 |
0.19 |
0.00 |
21.65 |
1.75 |
|
регион9 |
28.4 |
0.86 |
0.00 |
0.09 |
0.05 |
26.78 |
1.62 |
|
регион10 |
25.5 |
0.77 |
0.00 |
0.23 |
0.00 |
25.50 |
0.00 |