Глава 3. Применение символьного анализа в информационно аналитических системах

3.1 Множественная линейная регрессия

Пусть все входные данные 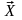являются числовыми, и целевая переменная 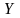тоже числовая. Тогда для каждой записи можно построить модель:

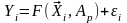, (3.1)

где 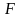- функция зависимости целевой переменной от входных данных и некоторых параметров, 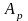- параметры регрессии, а 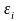- шум, ошибки.

Необходимо найти наилучшую функцию и наилучшие параметры таким образом, чтобы ошибки были достаточно малы. Накладывается условие: 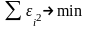. Тогда это уже задача нахождения минимальной функции:

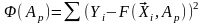. (3.2)

Замечание: Если точки сильно «раскачиваются», выбиваются из распределений, то в последней формуле правильнее выбирать не сумму квадратов, а сумму модулей.

Существует определенный класс функций, для которых эта задача может быть решена с помощью простых матричных вычислений. Это функции линейные относительно :

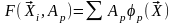. (3.3)

В этом случае получается система линейных уравнений, которая может быть решена с помощью матричных вычислений. Самый простой выбор функции 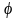в виде значения одной из входных переменных. В результате мы получаем модель линейной регрессии:[31]

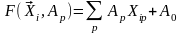. (3.4)

Для определения набора значимых входных переменных для нашей модели исполняем следующий алгоритм:

На первом шаге алгоритма этот набор переменных пуст. Решаем регрессионную задачу отдельно для каждой переменной. Получаем одномерные регрессионные модели, количество которых равно количеству переменных. Для каждой модели вычисляем свою стандартную ошибку: . После этого выбираем модель с наименьшей стандартной ошибкой и переменную, входящую в эту модель, включаем в наш набор.

На следующем шаге мы строим двумерные регрессионные модели для двух переменных, одна из которых –переменная из нашего набора, а вторую переменную перебираем. Снова вычисляем стандартную ошибку для каждой модели, и включаем новую независимую переменную в наш набор.

Далее алгоритм продолжается.

Кроме стандартной ошибки необходимо проверять еще один критерий – случайность зависимости между данными. Существует два способа оценки этой случайности:

1. Статистика Фишера. С помощью матричных операций находим регрессионные коэффициенты и точность их определения 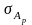. Статистика Фишера:

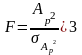. (3.5)

Если больше 3, то данная переменная является статистически значимой для нашей регрессионной модели. На определенном этапе, добавляя следующий параметр, возникнет ситуация, когда этот параметр не проходит тест Фишера. В этом случае мы прекращаем добавление новых параметров в наш набор.

2. Орномизированное тестирование. Входные переменные представлены прямоугольной таблицей, а целевая переменная столбцом данных. Делаем случайные перестановки в столбце , и получаем несколько новых столбцов 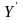. Для каждого такого столбца проводим решение регрессионной задачи, и получаем несколько ошибок 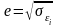. Обозначим ошибку для исходных значений 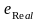, а ошибку каждого j-го столбца обозначим 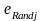. Если 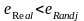, то определенная нами зависимость является статистически значимой.

Эту же процедуру можно использовать для определения значимости модели. Мерой значимости для этого метода является:

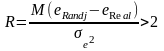. (3.6)

При выполнении этого условия установленная зависимость является статистически значимой.

Отметим, что критерий оценивает значимость для модели каждого критерия, а критерий оценивает значимость всей модели.

Существует еще один критерий оценки модели: вклад в сумму квадратов модели. Постепенно включая переменные в набор, мы уменьшаем ошибку модели. Ее уменьшение показывает, какую часть вероятности объясняет наша модель. Критерий: 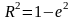. Но эта величина очень сильно зависит от корреляции данных, и поэтому является не очень объективной. Наиболее объективным является критерий .[32]

Замечание: по количеству записей этот метод является линейным, а по количеству полей – более сложный.