31 Вопрос. Достаточные признаки сходимости ( и расходимости) неотрицательных рядов: ограниченность частичных сумм, признаки сравнения, признаки Даламбера и Коши , интегральный признак Коши.

Признаки сравнения рядов

Пусть и 0≤

Тогда справедливы следующие признаки:

 Если сходится, то также сходится;

 Если расходится, то также расходится.

Предельный признак сравнения.

Если элементы знакоположительных рядов и сумма по n от 1 до ∞ , являются эквивалентами, числовыми последовательностями , то ряды сходятся и расходятся одновременно Если предел отношений общих пределов двух рядов =A является конечной величиной отличной от нуля , то исходный ряд сходится и расходится.

Признак Даламбера.

Пусть знакоположительный ряд(

Если существует –q, то при q [0;1) ряд сходится

При q (1 ) расходится .

Признак Коши.

Пусть - знакоположительный ряд.

Если существует 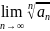=q, то при

q[0;1) ряд сходится q(1;+ ) ряд расходится q=1 требуются дополнительные условия.

Если придельные признаки не дают ответа, то нужно проверить 1.необходимый признак сходимости

=0 (

2.Признаки сравнения, интегральный признак Коши и др.

Интегральный признак Коши.

Если f (x)≥0 при x≥0, непрерывно монотонно убывает, то сходятся или расходятся одновременно.

1.

2.

Вопрос 32 Знакопеременные ряды .Признак Лейбница для знакочередующегося ряда. Оценка остатка ряда Лейбница.

Знакопеременный ряд называется знакочередующимся рядом, если два любых соседних члена ряда имеют разные знаки.

Cn , где Cn>0

Cn= Cn

Теорема Лейбница.

Если абсолютные величины элементов знакочередующегося ряда Cn ( Cn>0) образуют монотонно-убывающую ( > сходящуюся к нулю ( ), то ряд сходится

Оценка остатка ряда Лейбница .

Знакочередующийся ряд, элементы которого удовлетворяют условия признака Лейбница называется рядом Лейбница.

Следствие. Теорема Лейбница

Погрешность получаемая при замене суммы ряда Лейбница его частичной суммой , но абсолютная величина не превосходит абсолютной величины первого отброшенного члена ряда.

≤

33 Вопрос. Абсолютная и условная сходимость знакопеременных рядов. Формулировка свойств абсолютно и условно сходящихся рядов. Признаки Даламбера и Коши для знакопеременных рядов.

(1)

модульный ряд (2)

≥0

-Знакопеременный ряд (1) является абсолютно сходящимся, если сходится его ряд модулей (2).

-Знакопеременный ряд (1) называется условно сходящимся , если ряд сходится, а ряд (2) расходится.

-расходится, если не существует или

Свойства знакопеременных рядов.

1.Абсолютно сходящийся ряд сходится- теорема о абсолютной сходимости ряда.

2.В абсолютно сходящемся ряду можно произвести образом перестановки и группировки, при этом поведение ряда не меняется и сумма не меняется.

3.Теорема Римана. В знакопеременном условно сходящемся ряду путем перестановки членов ряда можно получить ряд с любой наперед заданной суммой.

Признаки Даламбера и Коши для знакопеременных рядов.

Признак Даламбера.

Пусть - знакоположительный ряд.

Если q= существует, то при q<1, ряд сходится абсолютно; при q>1 ряд расходится.

Если q= существует, то при q<1 ряд сходится абсолютно, при q>1 ряд расхоится.

Замечание.

Если q не существует или q =1, то нужно использовать необходимый признак сходимости и признак сходимости или интегральный признак Коши для ряда модулей. q≥0.