
- •2. Несобственные интегралы 1-го и 2-го рода. Понятие сходящегося и расходящегося несобственного интеграла. Эталонные несобственные интегралы.
- •3. Определение функции многих переменных (фмп). Предел и непрерывность в точке фмп. Свойства функций, непрерывных в точке.
- •5. Дифференцируемость фмп в точке. Дифференциал фмп. Необходимые условия дифференцируемости в точке.
- •6. Достаточные условия дифференцируемости функции многих переменных в точке.
- •7. Дифференцирование сложных функций. Теорема о производной сложной функции.
- •8. Скалярное поле. Поверхности и линии уровня. Определение и вычисление производной скалярного поля по направлению. Градиент скалярного поля, определение и свойства.
- •9. Частные производные высших порядков. Формулировка теоремы о смешанной производной.
- •15. Двойной интеграл. Определение и свойства двойного интеграла. Его геометрический смысл. Условия существования двойного интеграла.
- •22 Вопрос. Интегрирование (решение) лоду n-го порядка с постоянными коэффициентами методом Эйлера
- •27 Вопрос Фундаментальная система решения (фср) лосу. Теорема об общем решении лосу.
- •28 Вопрос. Решение лосу с постоянными коэффициентами методом Эйлера.
- •29 Вопрос.
- •30 Вопрос
- •31 Вопрос. Достаточные признаки сходимости ( и расходимости) неотрицательных рядов: ограниченность частичных сумм, признаки сравнения, признаки Даламбера и Коши , интегральный признак Коши.
- •Вопрос 32 Знакопеременные ряды .Признак Лейбница для знакочередующегося ряда. Оценка остатка ряда Лейбница.
- •33 Вопрос. Абсолютная и условная сходимость знакопеременных рядов. Формулировка свойств абсолютно и условно сходящихся рядов. Признаки Даламбера и Коши для знакопеременных рядов.
- •34 Вопрос Степенные ряды. Теорема Абеля Теорема об области сходимости степенного ряда.
- •35 Вопрос. Ряды Тейлора и Маклорена. Теорема о единственности разложения. Теорема о необходимых и достаточных условиях разложимости; теорема о достаточных условиях разложимости функции в ряд Тейлора.
- •38 Вопрос. Комплексные ряды. Сходящиеся абсолютно сходящиеся и условно сходящиеся ряды. Формулы Эйлера.
22 Вопрос. Интегрирование (решение) лоду n-го порядка с постоянными коэффициентами методом Эйлера
I. +
+ =0
(1)
=0
(1)

 ,….
,…. (
числа).
y=
(
числа).
y= подстановка Эйлера (2)
y’=
,y’’=
подстановка Эйлера (2)
y’=
,y’’= ,….y=
,….y=
 +
+ =0
=0
 +
+ характеристическое уравнение.
1.
характеристическое уравнение.
1. = корень уравнения (3)
= корень уравнения (3)
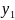 =
= ,
, =x
,……
=x
,……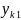 =
=
II.Пусть
 является комплексным корнем кратности.
является комплексным корнем кратности.
 =
= (также комплексный к.к)
этой паре
комплексных корней соответствует 2к-
частн.решений.
(также комплексный к.к)
этой паре
комплексных корней соответствует 2к-
частн.решений.
 =
= Можно
доказать, что решение соответствует
разным корням, линейно- независимое
между собой.
Можно
доказать, что решение соответствует
разным корням, линейно- независимое
между собой.
23
вопрос. Теорема об общем решении ЛНДУ
n-ого
порядка.
 =
= +
+ ,
где
:Ln[yn]=0
Общее
решение можно при помощи подбора
частного решения ЛНДУ и методом вариации.
,
где
:Ln[yn]=0
Общее
решение можно при помощи подбора
частного решения ЛНДУ и методом вариации.
24
вопрос. Метод
вариации и метод подбора решения ЛНДУ
n-ого
порядка.
Метод
подбора.
Ln[y]=f(x),
 ,….
,…. –действительные числа.
f(x)=
–действительные числа.
f(x)= (P
(P (x)
(x) +Q
+Q (x)
(x) ),
то
=
(
),
то
=
( (x)
+Re(x)
(x)
+Re(x) I=max
I=max (x)=
(x)=
 =
= +…+
+…+
 r=0,
если
r=0,
если
 не является корнем характеристического
уравнения для соответств.ЛОДУ.
r=R,
если
является корнем кратности.
не является корнем характеристического
уравнения для соответств.ЛОДУ.
r=R,
если
является корнем кратности.
Метод
вариации.
Постоянные
переменные применимы к уравнениям с
переменными коэффициентами для которых
фундаментальна система решений в
элемент. Функц. Ln[y]=f(x).
 -ФСР
ЛОДУ Ln[y]=0
-ФСР
ЛОДУ Ln[y]=0
 =
= (x)
+
(x)
+ (x)
+…+
(x)
+…+ W(x)=
W(x)= =
= =
=
W(x)= =>
=>
25 вопрос. Определение дифференциального уравнения и связанных с ним общих понятий.
Дифференциальным уравнением называется такое уравнение, которое содержит производные от искомой функции и может содержать искомую функцию и независимую переменную. Уравнение вида F (x, y (x), y ' (x), …, y (n)(x)) = 0, где x — независимая действительная переменная, y (x) — искомая функция, называется обыкновенным дифференциальным уравнением. Если уравнение содержит несколько независимых переменных, искомую функцию и частные производные от искомой функции по независимым переменным, например
X
 —
— =
0, z
= z
(x,
y),
то оно называется уравнением
с частными производными.
=
0, z
= z
(x,
y),
то оно называется уравнением
с частными производными.
В дальнейшем будем рассматривать только обыкновенные дифференциальные уравнения. Порядком дифференциального уравнения называется наивысший порядок, входящих в него производных. Решением дифференциального уравнения называется всякая функция y = φ (x), которая при подстановке в уравнение обращает его в верное равенство. График решения дифференциального уравнения называется интегральной кривой этого уравнения. Процесс нахождения решения дифференциального уравнения называется интегрированием этого уравнения. Не всегда удается получать решения в явном виде, например x2 + y2 = C.
Решение дифференциального уравнения, полученное в неявном виде F (x, y) = 0, называется интегралом дифференциального уравнения. Общим решением дифференциального уравнения называется такое его решение, содержащее произвольные постоянные, из которого любое частное решение может быть получено при соответствующем подборе произвольных постоянных. Частное решение дифференциального уравнения — это решение, не содержащее произвольных постоянных. Аналогично определяются общий интеграл и частный интеграл дифференциального уравнения. Если уравнение не интегрируется в элементарных функциях, но все его решения выражаются через неопределенные интегралы от элементарных функций, то говорят, что уравнение проинтегрировано в квадратурах. Квадратурой называется операция взятия неопределенного интеграла.
Например,
все решения уравнения y'
=
 даются формулой y
=
даются формулой y
=
 dx
+ C.
dx
+ C.
Постановка
задачи Коши для нормальной системы
дифференциальных уравнений.
Задача
Коши состоит в отыскании такого решения
системы, которое удовлетворяет заданное
начальное условие.

Общим
решение называется такой набор функций,
который при любых значениях коэффициентов
удовлетворяет системе и при любых
начальных условиях, где
 существует единственный набор
коэффициентов
существует единственный набор
коэффициентов
 ,
, при которых выполнены начальные условия
при которых выполнены начальные условия
Линейные
системы дифференциальных уравнений.
 линейная
система дифуров в нормальном виде
линейная
система дифуров в нормальном виде
 -диф
уравнение.
-диф
уравнение.
 называется решением системы, если при
подстановке функции в систему получается
верное равенство
Y(x)=
называется решением системы, если при
подстановке функции в систему получается
верное равенство
Y(x)= =
= -вектор
функции или векторная функция.
-вектор
функции или векторная функция.
Векторно-матричная
форма записи.
A=(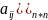 F(x)=(
F(x)=( V=
V= Y’=
Y’= Арнольд.
L[Y]=Y’-AY|
L[Y]=F(x);
[L]-оператор.
Всякая
система линейных дифуров n-ого
порядка может быть сведена к решению
дифуров порядка не выше n-ого
и обратно.
Всякое диф.уравнение n-ого
порядка может быть сведена к системе.
Арнольд.
L[Y]=Y’-AY|
L[Y]=F(x);
[L]-оператор.
Всякая
система линейных дифуров n-ого
порядка может быть сведена к решению
дифуров порядка не выше n-ого
и обратно.
Всякое диф.уравнение n-ого
порядка может быть сведена к системе.
