1. Геометрические приложения определенного интеграла Площади плоских фигур

1)

2)

3)

Длин дуг плоских и пространственных кривых

1)

2)

3)

Вычисление объемов тел по площади поперечного сечения и тел вращения

1)

2)

Площадей поверхностей тел вращения

2. Несобственные интегралы 1-го и 2-го рода. Понятие сходящегося и расходящегося несобственного интеграла. Эталонные несобственные интегралы.

Несобственный интеграл 1 рода – это интеграл по бесконечному промежутку под ограниченной функцией.

Несобственный интеграл 1 рода называется сходящимся, если существует конечный предел частичных интегралов.

Несобственный интеграл 2 рода – это интеграл по конечному промежутку под неограниченной функцией.

Несобственный интеграл 2 рода с особенностью на правой границе называется сходящимся, если существует предел частичных интегралов.

Эталонный интеграл

3. Определение функции многих переменных (фмп). Предел и непрерывность в точке фмп. Свойства функций, непрерывных в точке.

Опр. Переменная z называется функцией 2-х переменных x и y, если по некоторому закону каждой паре из некоторого множества ставится в соответствие вполне определенное значение z.

Функция f(x₁,...,x_n) имеет пределом число A при стремлении переменных x₁,...,x_n, соответственно, к a₁,...,a_n, если для каждого число  найдется такое число  , что   , то есть

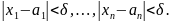
Функция называется непрерывной в точке , если верно равенство .

Св-ва:

1) Пусть функции f(x) и g(x) непрерывны в точке x₀. Тогда функции h₁(x)=f(x)+g(x), h₂(x)=f(x)-g(x), h₃(x)=f(x)g(x) непрерывны в точке x₀. Если  , то функция   также непрерывна в точке x₀.

2) Пусть функции f и g таковы, что существует композиция h(x)=(f o g)(x)=f(g(x)), x D(g). Пусть функция g непрерывна в точке x₀ D(g), а функция f непрерывна в соответствующей точке u₀=g(x₀)  . Тогда композиция h=f o g непрерывна в точке x₀.

3) Пусть функции f(x) и g(x) непрерывны слева (справа) в точке x₀. Тогда функции h₁(x)=f(x)+g(x), h₂(x)=f(x)-g(x), h₁(x)=f(x)g(x) непрерывны слева (соотв. справа) в точке x₀. Если  , то функция     также непрерывна слева (спpава) в точке x₀.

4. Частные производные ФМП. Геометрический смысл частных производных функции двух переменных z=f(x, y). Касательная плоскость и нормаль к поверхности, заданной явно уравнением z=f(x, y).

Частная производная - производная функции двух или более независимых переменных по любой из них при фиксированных остальных.

Геом. смысл:

Проведем через точку М₀, принадлежащую поверхности, плоскость, параллельную плоскости zoy. Тогда в сечении мы получим некоторую кривую. Проведем к ней касательную. Угловой коэффициент этой касательной k_кас=tga=f’_y(x₀, y₀).

Нормаль: =

Касательная:

5. Дифференцируемость фмп в точке. Дифференциал фмп. Необходимые условия дифференцируемости в точке.

Функция z=f(x, y) называется дифференцируемой в точке , если ее полное приращение , где А и В – конечные величины, независящие от , – бесконечно малое высшего порядка малости по при

Если функция z=f(x, y) дифференцируема в точке P₀ , то главная, линейная относительно приращения аргументов, часть ее полного приращения называется полным дифференциалом функции и обозначается

.

Необходимые условия:

Если функция дифференцируема в точке, то она непрерывна в этой точке.