8.3. Центры тяжести простейших фигур

1. Центр тяжести треугольника. Рассмотрим треугольник, лежащий в плоскости Oxy, координаты вершин которого известны: A_i (x_i,y_i) , (i = 1,2,3) .

Разбивая треугольник на узкие полоски, параллельные стороне А₁А₂ , придем к выводу, что центр тяжести треугольника должен принадлежать медиане А₃ М₃ (Рис.8.3)_.

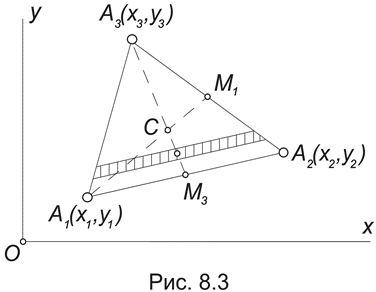
Разбивая треугольник на полоски, параллельные стороне А₂А₃, можно убедиться, что он должен лежать на медиане А₁М₁. Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан, которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.

В частности, для медианы А₁М₁ получим, учитывая, что координаты точки М₁  это среднее арифметическое координат вершин А₂ и А₃ :

x_c = x₁ + (2/3)(x_М1  x₁) = x₁ + (2/3) [(x₂ + x₃) /2  x₁] = (x₁+ x₂ +x₃)/3.

Таким образом, координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин:

x_c = (1/3)x_i ; y_c = (1/3)y_i .

2. Центр тяжести кругового сектора. Рассмотрим сектор круга радиуса R с центральным углом 2, расположенный симметрично относительно оси Ox (Рис.8.4) .

Очевидно, что y_c = 0, а расстояние от центра круга, из которого вырезан этот сектор, до его центра тяжести можно определить по формуле (8.2):

x_c = . (8.5)

Проще всего этот интеграл вычислить, разбивая область интегрирования на элементарные секторы с углом d. С точностью до бесконечно малых первого порядка такой сектор можно заменить треугольником с основанием, равным Rd и высотой R. Площадь такого треугольника dF = (1/2) R ² d, а его центр тяжести находится на расстоянии 2/3 R от вершины, поэтому в (8.5) положим x = (2/3)Rcos. Подставляя в (8.5) F =  R ², получим:

x_c = = = = =

= . (8.6)

С помощью последней формулы вычислим, в частности, расстояние до центра тяжести полукруга.

Подставляя в (8.6)  = /2, получим: x_c = (4R)/ (3)  0,4 R .

Литература

1. Куликов И.С., Трянина Н.Ю. Сборник задач по теоретической механике: Учебное пособие / И.С. Куликов, Н.Ю. Трянина. – Н.Новгород: Изд-во ННГАСУ, 2002. – 84с.

2. Мещерский И.В. Сборник задач по теоретической механике: Учебное пособие / И.В. Мещерский.  М.: Наука, 1986.  448 с.

3. Сб. заданий для курсовых работ по теоретической механике: Учебное пособие / Под ред. А.А.Яблонского.  М. Высш. школа, 1985  367 с.

4. Тарг С.М.. Краткий курс теоретической механики. Учебник для вузов/ С.М.Тарг.  10-е изд., перераб. и доп.  М.: Высшая школа, 1986.  478 с.

5. Теоретическая механика. Статика: учебное пособие / Е.Е. Антонов, Г.В.Аржаева, В.В. Родионов. Н.Новгород, ННГАСУ, 1998. – 91с.

6. Яблонский А.А., Никифорова В.М. Курс теоретической механики. ч.I. Статика. Кинематика. Учебник. Изд. 4-е, перераб. и посл. издания./ А.А. Яблонский, В.М. Никифорова.  М.: Высшая школа, 1971.  424 с.