21. Туннельный эффект

Тунне́льный эффект, туннели́рование — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовойприроды, невозможное и даже полностью противоречащее классической механике. Аналогом туннельного эффекта в волновой оптикеможет служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение.

Упрощённое объяснение

Туннельный эффект можно объяснить соотношением неопределённостей.^[1] Записанное в виде:

,

оно показывает, что при ограничении квантовой частицы по координате, то есть увеличении её определённости по x, её импульс p становится менее определённым. Случайным образом неопределённость импульса   может добавить частице энергии для преодоления барьера. Таким образом, с некоторой вероятностью квантовая частица может проникнуть через барьер, а средняя энергия частицы останется неизменной.

22. Частица в одномерной прямоугольной «потенциальной яме»

Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками».

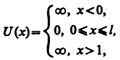
где l — ширина «ямы», а энергия отсчитывается от ее дна

Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде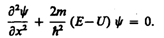

По условию задачи, частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения за пределами «ямы» равна нулю. На границах «ямы» (при х=0 и х=1) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные усло­вия в данном случае имеют вид

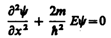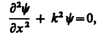В пределах «ямы» (0  х  l) уравнение Шредингера сведется к уравнению или где  

Общее решение дифференциального уравнения:

Тогда

Условие (l)=A sin kl = 0 выполняется только при kl = n, где n — целые числа, т. е. необходимо, чтобы

Из выражений (220.4) и (220.6) следует, что

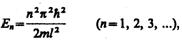
т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Е_n, зависящих от целого числа п. Следовательно, энергия Е_n частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е_n называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Е_n, или, как говорят, частица находится в квантовом состоянии n.

Постоянную интегрирования А найдем из условия нормировки (216.3), которое для данного случая запишется в виде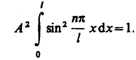

В результате интегрирования получим А = , а собственные функции будут иметь вид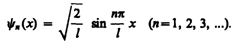

Из выражения вытекает, что энергетический интервал между двумя сосед­ними уровнями равен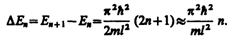

Таким образом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не накладывает.

Кроме того, квантово-механическое рассмотрение данной задачи приводит к выводу, что частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная . Неопределенность импульса ph/l. Такому разбросу значений импульса соответствует кинетическая энергия E_min(p)²/(2m) = h²/(2ml²).