Данные по личностной тревожности испытуемых до и после тренинга «Уверенное поведение»
-
ФИО
Личностная тревожность
до тренинга
после тренинга
1.И. В. Л.
5
5
2.Я. Е. А.
4
1
3.К С. И
4
4
4.Р М.Н.
4
4
5.Н.М.Т.
5
4
6.Е. Л.П.
6
5
7.Л. К. С.
3
5
8.Т. А. П.
6
5
9.Б. В. В
6
5
10.С М.А
5
6
11.В. П. Р.
6
6
12.Ч. Н. Г.
6
3
13.А.С.П.
3
1
14.В.С.К.
4
3
15.В.П.П.
4
3
16.Л.Г.Т.
4
4
17.Т.И.Ч.
4
4
М (среднее)
4,65
4
D (дисперсия)
1,12
2,12
SD(стандартное
отклонение)
1,06
1,46
А (ассиметрия)
0,10
-0,82
Е (эксцесс)
-1,27
0,42
Для первой выборки (до начала тренинга «Уверенное поведение») проведем расчеты для его участников, применив методику Плохинского Н.А.
Сформулируем гипотезы:
Нулевая гипотеза (Н0) — распределение эмпирической случайной величины данных, измеренных до проведения тренинга, отличается от нормального закона распределения.
Альтернативная гипотеза (Н1) — распределение эмпирической случайной величины подчиняется нормальному закону распределения.
Применим критерии Плохинского.
А=0,10; ΔА= 0,548; qА =0,10/0,548 = 0,183 <3
E=-1,27; ΔЕ = 2*0,548 =1,095; qE= 1,27 / 1,095 = 1,159 <3, где ошибки А и Е
По критерию Плохинского эмпирическое распределение достоверно можно считать распределенным нормально.
Акр= 1,549 Екр=3,876
А< Акр (0.1 <1.549) ; Е< Екр (1,27 <3,876)
Для второй выборки (после тренинга «Уверенное поведение») применим двойной составной критерий.
Сформулируем гипотезы:
Нулевая гипотеза (Н0) — распределение эмпирической случайной величины данных, измеренных после проведения тренинга, отличается от нормального закона распределения.
Альтернативная гипотеза (Н1) — распределение эмпирической случайной величины подчиняется нормальному закону распределения
Проверим выполнение первого условия Двойного критерия.
Проведем сравнение. Для этого необходимо рассчитать dэмп.
Сначала найдем среднее значение x=4.
Дополним таблицу 9 несколькими столбцами (Таблица 10):
Таблица 10
-
ФИО
Личностная
тревожность
после тренинга
|x -
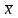|(|x - |)2
1.И. В. Л.
5
1
1
0
2.Я. Е. А.
1
3
9
0
3.К С. И
4
0
0
0
4.Р М.Н.
4
0
0
0
5.Н.М.Т.
4
0
0
0
6.Е. Л.П.
5
1
1
0
7.Л. К. С.
5
1
1
0
8.Т. А. П.
5
1
1
0
9.Б. В. В
5
1
1
0
10.С М.А
6
2
4
0
11.В. П. Р.
6
2
4
0
12.Ч. Н. Г.
3
1
1
0
13.А.С.П.
1
3
9
0
14.В.С.К.
3
1
1
0
15.В.П.П.
3
1
1
0
16.Л.Г.Т.
4
0
0
0
17.Т.И.Ч.
4
0
0
0
(среднее)
4
Сумма |x - |
18
Сумма (|x - |)2
34
D (дисперсия)
2,12
SD(стандартное
отклонение)
1,46
Заполним третий столбец таблицы 10: .|x - |
Просуммируем содержание столбца 1:
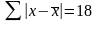
Затем найдем D и SD. Для этого возведем разность хпосле - после в квадрат и запишем в столбец 4. Подсчитаем сумму:
Поделим ее на (п — 1) = 17 — 1 = 16. Получим D = 2,12.
Возьмем квадратный корень из D:
Пользуясь формулой dэмп. рассчитываем
и получаем dэмп. = 0,75.
С помощью статистических таблиц определим d1 и d2 соответствующие объему выборки. d2= 0,6829, d1 = 0,9137
.Т.к. dэмп> d2 и dэмп< d1 (0,75 > 0,6829 и 0,75 < 0,9137) , то значит, dэмп удовлетворяет первому условию и можно переходить ко второму сравнению.
Проверим второе условие по двойному критерию.
Найдем z из статистических таблиц для объема выборки п = 17
z = 2,58.
Рассчитаем вспомогательное значение s, воспользовавшись рассчитанным стандартным отклонением SD,
s=SD·z, s = 1,46*·2,58 =3,76
Если значение в столбце 3 |x - | будет больше рассчитанного s =3,76, тов столбец 5 пишем 1, если нет, то 0. Затем считаем mэмп (сумму ячеек столбца 5): mэмп =0
По статистической таблице находим mкр: mкр=1
Сравниваем mкр и mэмп: mкр > mэмп.
Значит, второе условие выполняется, следовательно, принимается гипотеза H1
Ответ: Принимается гипотеза Н1. Данные учащихся после исследования можно считать распределенными по нормальному закону.
Более подробно с двойным составным критерием можно познакомиться, используя дополнительную литературу [2].