ПРИМЕРЫ РЕШЕНИЯ И ЗАДАЧИ

ДЛЯ САМОСТОЯТЕЛЬНОЙ

РАБОТЫ

ОПИСАТЕЛЬНАЯ СТАТИСТИКА

Задача группирования данных в психологическом исследовании

Данная работа связана с подсчетами значений по формулам и графическим отображением данных, использованием библиотеки стандартных функций, Пакета анализа.

Работа с Пакетом анализа проводится следующим образом:

1. Выполняется команда Сервис / Анализ данных;

2. Из списка доступных инструментов анализа выбирается необходимый в данном случае и нажимается кнопка OK;

3. В диалоговом окне указываются

   1. Входные данные, включающие в себя:

      • Входной диапазон

      • Указатель наличия или отсутствия меток(заголовков). Если входной диапазон содержит заголовки столбцов, то ставим флажок в строке Метки

   2. Параметры вывода:

      • Местоположение полученных результатов, - установив переключатель либо в положение выходной интервал и указав адрес ячейки, куда поместить результат (если результат должен находиться на том же листе), либо в положение новый рабочий лист, либо в положение новая рабочая книга:

      • Необходимые результаты, - поставив флажок рядом с нужной строкой.

Замечание. Если команда Анализ данных отсутствует в пункте меню Сервис, необходимо выполнить следующие действия:

1. В пункте меню Сервис выбрать команду Надстройки,

2. Установить флажок Пакет анализа.

Ранжированный ряд

Используем функцию РАНГ в электронных таблицах MS EXCEL.

Функция Ранг возвращает ранг числа в списке чисел. Ранг числа — это его величина относительно других значений в списке. (Если список отсортировать, то ранг числа будет его позицией.)

Синтаксис: РАНГ (число; ссылка; порядок),

где число— число, для которого определяется ранг; ссылка— массив или ссылка на список чисел (нечисловые значения в ссылке игнорируются); порядок — число, определяющее способ упорядочения.

• Если порядок равен 0 (нулю) или опущен, то Microsoft Excel определяет ранг числа так, как если бы ссылка была списком, отсортированным в порядке убывания.

• Если порядок — любое ненулевое число, то Microsoft Excel определяет ранг числа так, как если бы ссылка была списком, отсортированным в порядке возрастания.

Заметки

• Функция РАНГ присваивает повторяющимся числам одинаковый ранг. Однако наличие повторяющихся чисел влияет на ранги последующих чисел. Например, если в списке целых чисел, отсортированных по возрастанию, дважды встречается число 10, имеющее ранг 5, число 11 будет иметь ранг 7 (ни одно из чисел не будет иметь ранг 6).

• Может оказаться необходимым использовать определение ранга, с учетом связей в учетной записи. Это можно осуществить, добавляя поправочный коэффициент в значение, возвращаемое РАНГ. Данный поправочный коэффициент подходит и для случая, когда ранг вычисляется в порядке убывания (порядок равен 0 или опущен), и в порядке возрастания (порядок равен ненулевому числу).

• Поправочный коэффициент для связанных рангов = [СЧЕТ(ссылка) + 1 – РАНГ(число, ссылка, 0) – РАНГ(число, ссылка, 1)]/2.

• Ранг, пересмотренный с учетом связей в учетной записи, равен значению функции РАНГ плюс поправочный коэффициент. Если число появляется в ссылке только один раз, поправочный коэффициент будет равен нулю.

• Для избежания ошибок ранжирования необходимо проводить проверку правильности реализации этой процедуры. Если ранжируются N признаков, то

Сумма рангов = 1+2+…+N = N*(N+1)/2

Пример 1. Имеется совокупность значений переменной X:111, 107, 123, 122,117, 117, 105, 108, 114, 102, 104. Необходимо проранжировать эти показатели.

Решение представлено в таблице 1.

Таблица 1

A	B	C	D	E	F
1	№ испытуемого	X	значение функции РАНГ с порядком 0	значение функции РАНГ с порядком 1	поправка	ранг
2	1	113	6	6	0	6
3	2	107	8	4	0	8
4	3	123	1	11	0	1
5	4	122	2	10	0	2
6	5	117	3	8	0,5	3,5
7	6	117	3	8	0,5	3,5
8	7	105	9	3	0	9
9	8	108	7	5	0	7
10	9	114	5	7	0	5
11	10	102	11	1	0	11
12	11	104	10	2	0	10

Поскольку сумма рангов равна 66 и N*(N+1)/2=11*12/2=66, то ранжирование проведено верно.

Построение распределения сгруппированных частот

Если выборка испытуемых значительна, то используют построение распределения сгруппированных частот.

Алгоритм построения распределения сгруппированных частот включает следующие этапы:

1. Определение размаха.

2. Выбор числа интервалов в зависимости от объема выборки (Таблица 2).

3. Определение границ разрядов.

4. Табулирование.

Таблица 2

Число разрядных интервалов в зависимости от объема выборки

Объем выборки	25-40	40-60	60-100	100-200	более 200
Число интервалов	5-6	6-8	7-10	8-12	10-15

Пример 2. Имеется совокупность значений переменной X: 4, 6, 5, 9, 9, 9, 8, 4, 4, 9, 7, 7, 6, 10, 8, 6, 8, 4, 6, 10, 7, 4, 7, 6, 6, 4, 6, 7, 8

Построить распределениие их частот.

1. Определим максимум и минимум, используя стандартные функции МИН и МАКС, соответственно: МИН=4, МАКС = 10,

Размах = Макс – Мин +1 = 10-4+1 = 7

2. Объём выборки = 29

3. По таблице 2 числа разрядных интервалов в зависимости от выборки находим число интервалов = 6

4. Определим шаг по формуле:

Шаг = Размах / Число_интервалов =7/6 = 1,166667

5. Определим границы разрядов и частоту попадания значений переменной X в полученные интервалы (Таблица 3). Для этого используем инструмент Гистограмма из Пакета анализа (в разделе параметры вывода поставить флажок в строке Вывод_графика)

Таблица 3

Распределение частот по интервалам

	границы интервалов			интервалы	частоты
	3,5			(3,5;4,66)	6
	4,666667			(4,66:5,83)	1
	5,833333			(5,83; 7)	11
	7			(7;8,16)	2
	8,166667			(8,16; 9,33)	4
	9,333333			9,33; 10,5)	2
	10,5

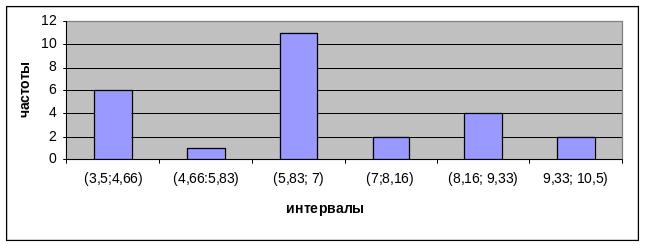
Рис. 1

Задачи для самостоятельного решения

Задача 1. В ходе исследования измерен уровень вербального интеллекта у респондентов возраста 16-17 лет: юношей (выборка А) и девушек (выборка В) (табл.4). Построить ряд сгруппированных частот. Проверить распределение на нормальность.

Таблица 4

Показатели вербального интеллекта

№	А	В	№	А	В	№	А	В
1	112	117	7	107	100	13	114	105
2	115	105	8	90	107	14	114	115
3	102	114	9	122	115	15	118	109
4	108	108	10	118	98	16	99
5	117	99	11	100	117	17	102
6	98	120	12	92	114

Задача 2. По методике Басса-Дарки исследован уровень агрессивности среди подростков 13-15 лет из различных семей: благополучных (выборка А) и неполных (выборка В) (табл. 5). Построить ряд сгруппированных частот. Проверить распределение на нормальность.

Таблица 5.