3 Кодирование

3.1 Уточнение структуры входных и выходных данных и определение ассемблерного формата их представления

Представим структуры входных и выходных данных в виде таблицы

Таблица входных и выходных данных приведена в приложении Б.

Таблица 3. 1. – Структуры входных и выходных данных

Модуль	Имя переменной	Значение	Формат
Main	x0	6.0	dd
	I1	24.6	dd
	I2	80.4	dd
	L	93.0	dd
	Xn	99.0	dd
	X	0.0	dd
	Y	0.0	dd
	n	150.0	dd
	vdX	0.0	dd
	Arrey	151 dup	AR
v_simvol	a1	0	dq
	pow_dec	0	dw
	i_save	0	dd
	f_save	0.0	dq
	c_05	0.5	dd
	c_10	10.0	dd
	i_tol	10	dw
	i_part	0	dw
	f_part	0	dt
	flag	0	db
	m_sign	0	db
	p_sign	0	db
	string	20 dup<“ ”>	db
in_float	NumTmp	0	dw
	cn10	10	dd
	cn48	48	dd

3.2 Программирование задачи

Программная реализация данной задачи содержится в приложении А данного курсового проекта, где представлены листинги с соответствующими комментариями.

4 Отладка и тестирование

4.1 Обнаружение, локализация и устранение ошибок в программе, выявленных в текстах

Отладка и тестирование производятся в отладчике, где при возникновении ошибки пользователь может отследить ее устранить в соответствии с установленными правилами синтаксиса языка Assembler.

Таблица 4.1. – Ошибки

Ошибка	Вид ошибки	Устранение
Need expression	FLD Arrey[si] Синтаксическая ошибка Не указано поле	FLD Arrey[si].vX
Illegal indexing mode	mov eax,Arrey[si*8].vX Ошибка адресации.	mov eax,Arrey[si].vX

В программе возникали также незначительные синтаксические ошибки, которые не стоят внимательного рассмотрения.

Полученный программный продукт полностью соответствует поставленной за­даче, хотя и не является идеальным, так как он не лишён многих недостатков. Вот некоторые из них:

1) Одним из недостатков данного программного продукта является необхо­димость явного указания того, что вводимое число является веществен­ным. Например, для ввода числа «2» необходимо ввести «2.0». Решени­ем данной проблемы может быть изменение алгоритма преобразования числа, вводимого с клавиатуры, в его двоичный эквивалент.

2) Следующим недостатком является невысокая точность вычислений. Это связано с тем, что все вещественные числа в программе представлены в коротком (32 бита) формате. Для повышения точности вычисления необ­ходимо использовать расширенный формат представления веществен­ных чисел (64 бита).

При тестировании определяли точность работы нашей программы и проводили с учётом зависимости погрешности значений от количества разбиений интервала.

Тестирование проводили путём изменения количества разбиений интервала и проверки полученного значения Y с помощью программы MathCAD.

По полученным данным (табл.4.1.2.-4.1.4.) построили графики зависимости погрешности значений от количества разбиений интервала (рис. 4.1.1.-4.1.3.). На графиках видно, что при увеличении количества разбиений интервала, погрешность уменьшается, значит программа работает верно.

Таблица 4.2.

1-й интервал
Кол-во интервалов	Полученное значение	Введенное число	Истинное значение	Погрешность
10	0,35695029			42,780116
30	0,307754446			23,10177852
50	0,280413658	20	0,25	12,16546328
70	0,2633504037			5,34016148
90	0,2517427139			0,69708556
100	0,2514255034			0,570201356

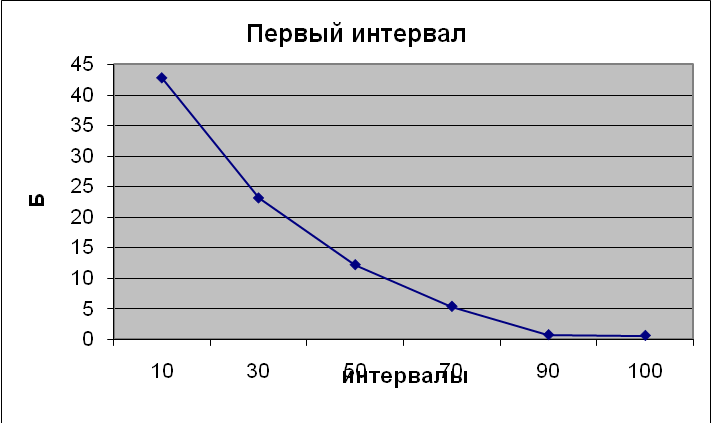
Рис. 4.1. – График зависимости погрешностей на 1-ом интервале.

Таблица 4.3.

2-й интервал
Кол-во интервалов	Полученное значение	Введенное число	Истинное значение	Погрешность
10	0,03780605			61,89780261
30	0,092			7,279333333
50	0,099283057	110	0,099222755	-0,06077428
70	0,099312708			-0,090657988
90	0,09924271			-0,020111188
100	0,099313634			-0,091590332

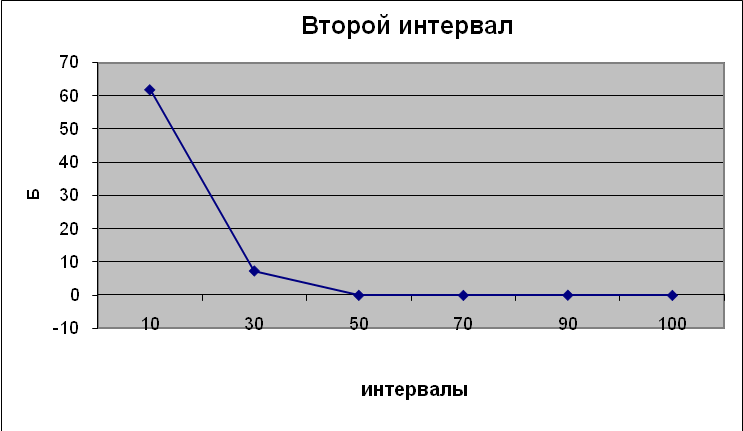
Рис. 4.2. – График зависимости погрешностей на 2-ом интервале.

Таблица 4.4.

3-й интервал
Кол-во интервалов	Полученное значение	Введенное число	Истинное значение	Погрешность
10	0,159999642			0,00022375
30	0,159999642			0,00022375
50	0,159999642	310	0,16	0,00022375
70	0,159999642			0,00022375
90	0,159999642			0,00022375
100	0,159999642			0,00022375

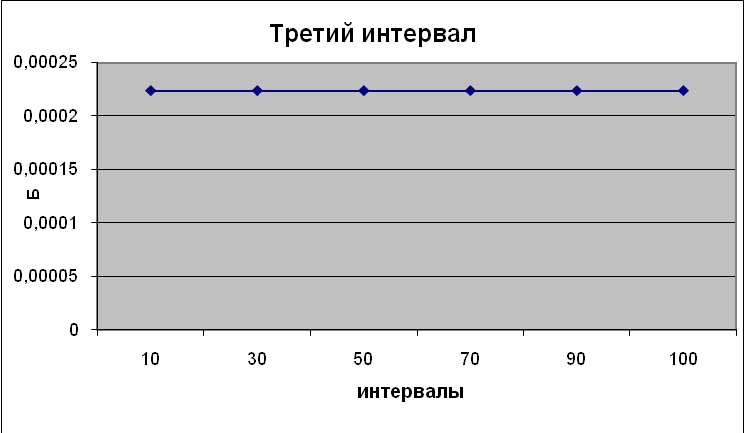
Рис. 4.3. – График зависимости погрешностей на 3-ем интервале.