
- •Введение
- •1 Постановка и формулировка задачи
- •1.2 Формулирование требований к представлению исходных данных и выходных результатов.
- •2 Проектирование
- •3 Кодирование
- •3.1 Уточнение структуры входных и выходных данных и определение ассемблерного формата их представления
- •4 Отладка и тестирование
- •5 Список используемой литературы
- •Приложение а
- •Приложение б
- •2. Функциональное назначение
- •3. Описание логической структуры
- •4. Вызов и загрузка
- •5. Входные и выходные данные

Введение
Данная курсовая работа состоит в создании законченного программного продукта, выполняющего вычисление заданного количества значений функции вида y = f(x), в определённом интервале значений X. Количество значений (число интервалов разбиения) вводится пользователем с клавиатуры при поступлении соответствующего запроса. Максимальное число интервалов – 100. Программно проверяются введенные значение на соответствие тому или иному интервалу. Функция является разрывной и состоит из трёх частей, определённых на интервалах заданной величины. После вычисления значения Y заносятся в оперативную память последовательно, для каждого значения выделяется по 4 байта. Поиск нужного значения осуществляется путём задания величины смещения от начала таблицы (массива данных). Этот способ обеспечивает существенную экономию оперативной памяти (почти в два раза), так как не требует хранения соответствующих значений Х. После этого пользователю предлагается ввести значение X в определённом диапазоне значений. Далее, путём интерполирования, опираясь на заполненную структуру данных, производиться вычисление значения функции для введённого значения X. Результат вычисления выводиться на экран.
Программа написана на языке Assembler с использованием функций математического сопроцессора.
При разработке программы использовались следующие программные продукты:
1) Файловый и архивный менеджер FAR для написания кода программы.
2) Пакет Turbo Assembler 5.0 для трансляции и компоновки программы.
3) Microsoft Word, используемый для написания исходного кода программы.
1 Постановка и формулировка задачи
1.1 Задание на разработку программного продукта
Программа, которую
необходимо разработать в процессе
выполнения курсовой работы должна по
полученной формульной зависимости вида
![]() сформировать программный продукт,
который бы выполнял следующие функции:
сформировать программный продукт,
который бы выполнял следующие функции:
В данной курсовой работе необходимо по полученной формульной зависимости вида сформировать программный продукт, который бы выполнял следующие функции:
Запрашивал у пользователя количество участков разбиения интервала n;
запрашивал у пользователя начальное значение
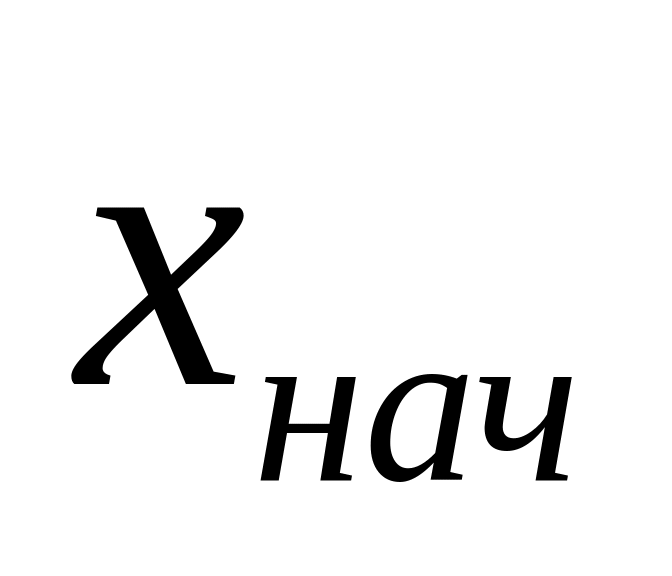 и шаг изменения этого параметра
и шаг изменения этого параметра
 ;
;производила вычисление значений функции
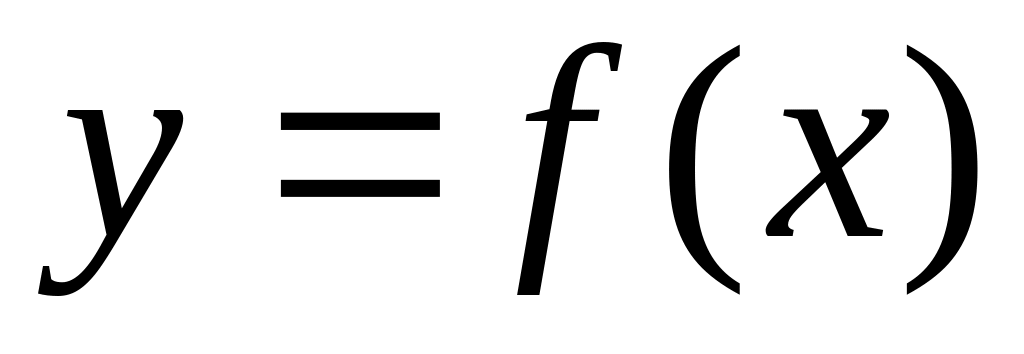 для всех
для всех
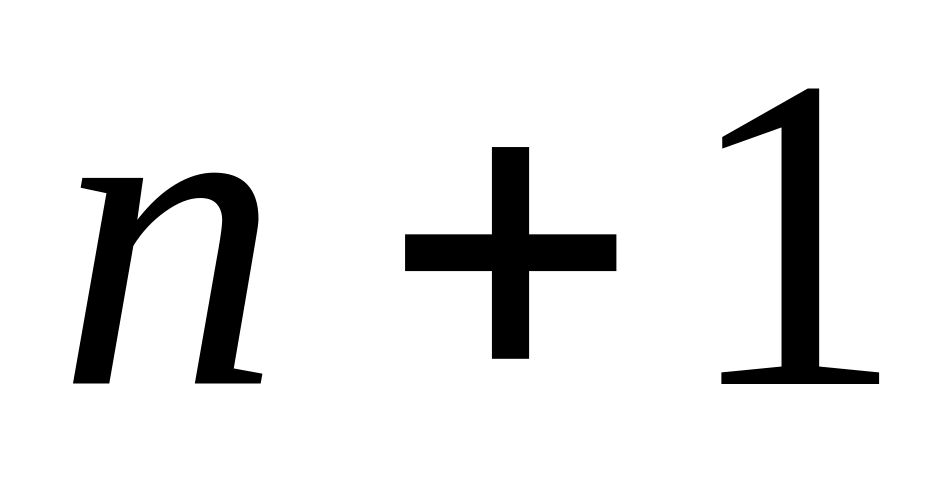 значений аргумента
значений аргумента
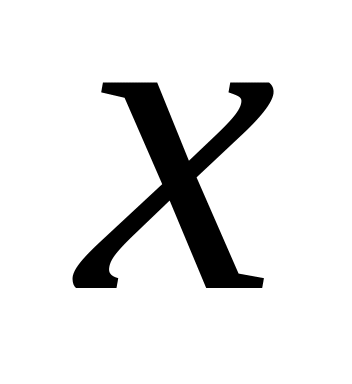 от
от
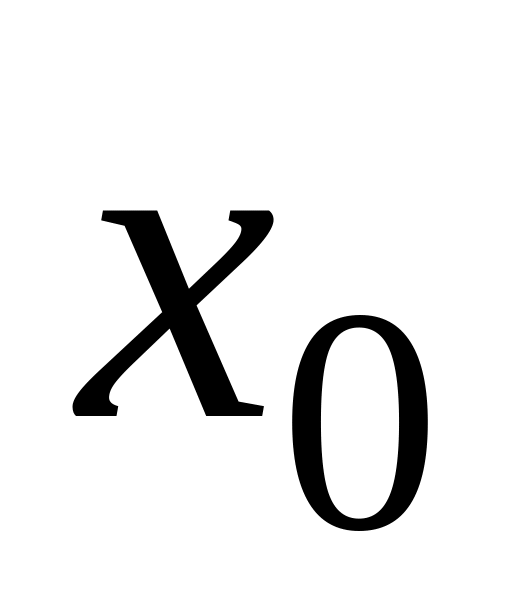 =
15,9 до
=
15,9 до
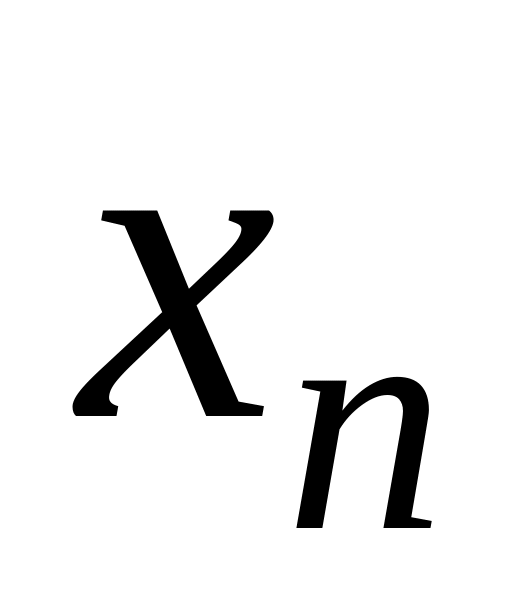 =
263
=
263
Первый интервал (x0 x x0+0.2l) y(x)=хsin(x)
Второй интервал (x0+0.2l< x x0+0.6l) y(x)=sin х2
Третий интервал (x0+0.6l< x xn) y(x)=х3
где l = xn - x0 –длина общего интервала;
занесение пар значений х, у в структуру хранения данных;
вывести на экран приглашения для ввода значения параметра х с указанием пределов варьирования;
по введенному значению х вычислить функцию , опираясь на данные структуры путем интерполяции;
вывести результат на экран в требуемом формате;
запрос на повторение действий в формате «Y/N».
Программа должна быть оформлена с использованием процедур.
1.2 Формулирование требований к представлению исходных данных и выходных результатов.
Исходные данные и выходные результаты должны быть представлены в формате вещественных чисел с плавающей точкой. Для изображения чисел c плавающей точкой в сопроцессоре существует три формата данных. Короткий формат имеет 32 бита, а длинный 64 бита. Третий формат определяет 80-битовые числа. Сопроцессор использует такой формат "промежуточного действительного числа", чтобы обеспечить очень высокую точность для промежуточных результатов вычислений.
Целые числа — лучший способ представления многих величин. Целые числа просто понимать и использовать, а также легко преобразовывать в двоичное представление. Однако c целыми числами плохо работать в случае очень больших значений. Очень большое целое число обычно оканчивается длинной строкой нулей. Целые числа, кроме того, не способны представить значение, содержащее дробную часть, т. e. ЭВМ не может запомнить число 1/2 в целом представлении. Любые другие дроби, меньше 1, также невозможно представить, используя целые числа.
Ученые и математики давным-давно разработали способ представления этих чисел в достаточно удобном виде. На первом этапе вводится десятичная точка (.), которая будет показывать границу между целой и дробной частями числа. В случае целого числа позиция, представляющая единицы, всегда находится на правом краю числа; в случае, когда используется десятичная точка, цифры справа от нее представляют значения, меньше 1.
У целых чисел каждая позиция числа соответствует степени числа 10.
Десятичная точка показывает границу между позицией, соответствующей 100, и дробной частью. В дробной части позиции снова являются степенями числа 10, но теперь эти степени - отрицательные.
Поскольку каждая позиция десятичного числа отличается от соседней на степень числа 10, умножение числа на 10 эквивалентно сдвигу десятичной точки на одну позицию вправо. Аналогично деление на 10 сдвигает десятичную точку на позицию влево. Это свойство можно использовать для сдвига десятичной точки на соответствующее место: мы сдвигаем десятичную точку и одновременно корректируем число на ту же степень числа 10. Такое представление чисел называется представлением c плавающей точкой, поскольку десятичная точка "плавает" в числе; она больше не помечает абсолютное место между целой и дробной частями. Положение десятичной точки можно выбрать из соображений удобства, а затем умножить число на нужную степень числа 10, чтобы получить правильное значение.
Десятичное число c плавающей точкой состоит из двух частей. Значащая часть числа называется мантиссой. На практике мантисса обычно находится в пределах 1 < мантисса < 10. Другая часть числа c плавающей точкой - это порядок, степень, в которую нужно возвести число 10 перед умножением его на мантиссу, т. e. 9.3 х 107 имеет мантиссу 9.3 и порядок 7. Если основание системы счисления определено раз и навсегда, в нашем случае это 10, то для восстановления первоначального числа должны быть заданы только два числа — мантисса и порядок.
Двоичные числа c плавающей точкой изображаются аналогично десятичным; отличие заключается в том, что основание системы счисления здесь 2, а не 10. Мантисса имеет значения 1 < мантисса < 2, а порядок показывает степень числа 2
Для того чтобы сохранить максимальную точность, вычислительные машины почти всегда хранят мантиссу в нормализованном виде. Это означает, что мантисса есть число, лежащее между 1 и 2 (1 < мантисса < 2). Два соображения говорят в пользу нормализации. Во-первых, ни один незначащий 0 не дает никакого вклада в точность числа. (Это несправедливо для нулей, лежащих в конце числа; мы считаем, что число 1.000 более точно, чем число 1.0.) Если в мантиссе c плавающей точкой появились незначащие нули, точность числа падает. Во-вторых, способ хранения мантиссы числа c плавающей точкой подразумевает, что двоичная точка находится на фиксированном месте. Фактически подразумевается, что двоичная точка следует после первой двоичной цифры, т. e. нормализация мантиссы делает единичным первый бит, помещая тем самым значение мантиссы между 1 и 2. Для выполнения нормализации ЭВМ корректирует порядок числа на соответствующее значение.
Точно так же, как длина мантиссы числа определяет его точность, длина поля порядка определяет диапазон числа. Поле порядка содержит степень числа 2, и чем больше бит в этом поле, тем большее число может быть представлено.
Важно отметить, что, хотя диапазон и расширяется c увеличением числа бит порядка, точность не увеличивается. Значение порядка хранится не как значение число, представленное в дополнительном коде. Для упрощения вычислений значение порядка в ЭВМ хранится в виде смещенного числа. Это означает, что к действительному значению порядка прибавляется смещение перед записью его в память. Значение смещения выбрано так, чтобы допустить сравнение порядков. В частности, это полезно при сравнении двух чисел c плавающей точкой. Значения порядка и мантиссы записываются в одном элементе данных, причем порядок записывается перед мантиссой. В случае смещенного значения порядка программа может сравнивать числа побитно, начиная со старших позиций. Первое же неравенство показывает соотношение чисел, и больше не нужно учитывать никакие части чисел. Значение смещения определяется размером поля порядка.
1.3 Запись основных формул в формате ПОЛИЗ
Для того, чтобы написать программу для вычисления некоторого выражения, его необходимо предварительно преобразовать в удобный для программирования сопроцессора вид. Процесс преобразования напоминает подготовку выражения для метода трансляции, основанного на использовании обратной польской записи (ПОЛИЗ). Запись формул в формате ПОЛИЗ приведена в таблице 1.3.1.
Таблица 1.1.- Запись формул в формате ПОЛИЗ
Обычная формула |
Формат ПОЛИЗ |
xsinx |
XSINX ** |
Sin(x^2) |
X ХSIN * |
Х3 |
X Х X ** |
Использование польской записи в данном проекте обусловлено особенностью организации сопроцессора – хранением его операндов в стеке.
