5. Пример выполнения работы

Задание № 1. Описать математические методы и модели систем (постановка задачи, основные уравнения).

Дискретные детерминированные системы (конечные автоматы).

при дискретно-стохастическом подходе к формализации процесса функционирования системы S подход остается аналогичный рассмотренному конечному автомату, то влияние фактора стохастичности можно проследить разновидности таких автоматов, а именно на вероятностных (стохастических) автоматах.

В общем виде вероятностный автомат (англ. probabilistic automat) можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически.

множество G, элементами которого являются всевозможные пары , где х_i и z_s —-элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функции  и , то с их помощью осуществляются отображения и , то говорят, что определяет автомат детерминированного типа.

Введем в рассмотрение более общую математическую схему. Пусть Ф — множество всевозможных пар вида , где y_j — элемент выходного подмножества Y. Потребуем, чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:

При этом , где b_kj — вероятности перехода автомата в состояние z_k и появления на выходе сигнала y_j если он был в состоянии z_s и на его вход в этот момент времени поступил сигнал x_i. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G. Обозначим множество этих таблиц через В. Тогда четверка элементов называется вероятностным автоматом (Р - автоматом).

Пусть элементы множества G индуцируют некоторые законы распределения на подмножествах Y и Z, что можно представить соответственно в виде:

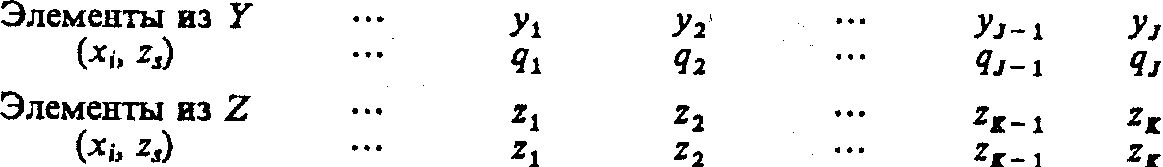
При этом и где z_k и q_k — вероятности перехода Р-автомата в состояние z_k и появления выходного сигнала у_k при условии, что Р-автомат находился в состоянии z_s и на его вход поступил входной сигнал х_i.

Если для всех k и j имеет место соотношение , то такой Р-автомат называется вероятностным автоматом Мили. Это требование означает выполнение условия независимости распределений для нового состояния Р-автомата и его выходного сигнала.

определение выходного сигнала Р-автомата зависит лишь от того состояния, в котором находится автомат в данном такте работы. Другими словами, пусть каждый элемент выходного подмножества Y индуцирует распределение вероятностей выходов, имеющее следующий вид:

Здесь , где s_i — вероятность появления выходного сигнала y_i при условии, что Р-автомат находился в состоянии z_k. для всех k и i имеет место соотношение , то такой Р-автомат называется вероятностным автоматом Мура.

Понятие Р-автоматов Мили и Мура введено по аналогии с детерминированным F-автоматом, задаваемым . Частным случаем Р-автомата, задаваемого как являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминированно. Если выходной сигнал Р-автомата определяется детерминированно, то такой автомат называется Y-детерминированным вероятностным автоматом. Аналогично, Z-детерминированным вероятностным автоматом называется Р-автомат, у которого выбор нового состояния является детерминированным.

Y-детерминированный Р-автомат задаётся таблицей переходов и таблицей выходов. Первую из этих таблиц можно представить в виде квадратной матрицы размерности КК, которую будем называть матрицей переходных вероятностей или просто матрицей переходов Р-автомата. В общем случае такая матрица переходов имеет вид

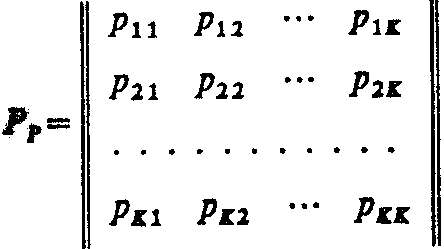
Для описания У-детерминированного Р-автомата необходимо задать начальное распределение вероятностей вида

Здесь d_k — вероятность того, что в начале работы Р-автомат находится в состоянии k. При этом . У-детерминированный Р-автомат можно задать в виде ориентированного графа, вершины которого сопоставляются состояниям автомата, а дуги — возможным переходам из одного состояния в другое. Дуги имеют веса, соответствующие вероятностям перехода р_ij, а около вершин графа пишутся значения выходных сигналов, индуцируемых этими состояниями.

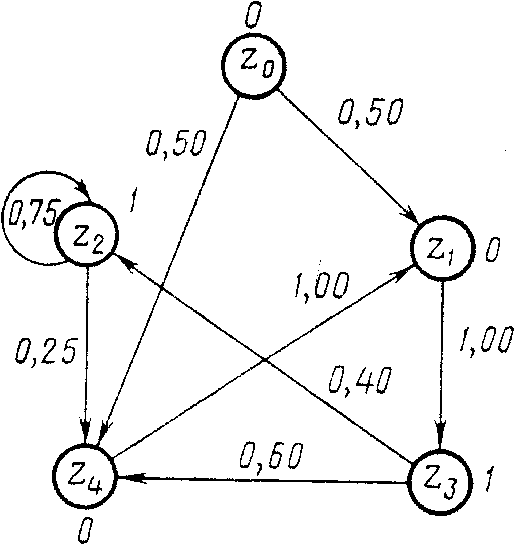
Р-автоматы могут использоваться как генераторы марковских последовательностей, которые необходимы при построении и реализации процессов функционирования систем S или воздействий внешней среды Е.

Для оценки различных характеристик исследуемых систем, представляемых в виде Р-схем, кроме случая аналитических моделей можно применять и имитационные модели, реализуемые, например, методом статистического моделирования.

Задание № 2. Осуществить кодирование методом Хаффмана заданной фразы:

Many a little makes a tickle

Решение:

Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева. Приведем общую схему построения дерева Хаффмана:

1. Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа).

2. Из списка выберем 2 узла с наименьшим весом.

3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.

4. Добавим сформированный узел к списку.

5. Если в списке больше одного узла, то повторить 2-5.

Построим дерево Хаффмана:

_ a t l e i m k s c y n

5 4 3 3 3 2 2 2 1 1 1 1

| | \ / \ / \ / 0\ 1/ 0\ 1/

| | \ / \ / \ / 2 2

| | 0\ 1/ 0\ 1/ 0\ 1/ 0\ 1/

| | 6 5 4 4

0\ 1/ 0\ 1/ 0\ 1/

9 11 8

\ | /

\ | /

0\ | 1/

| 17

0\ 1/

28

Двоичный код символов:

_ →100

a →101

t →000

l →001

e →010

i →011

m →1100

k →1101

s →11100

c →11101

y →11110

n →11111

Задание №3. Даны матрицы переходных характеристик. Определить вероятности состояний системы после заданного количества интервалов времени (N). Привести сигнальный граф системы и все вычисления. Начальные условия: Р₁(0)=1, Р₂(0)=Р₃(0)= ... =0. N=3

0,5	0,3	0,2
0	0,4	0,6
0	0	1

Решение:

К=1:

|0,5 0,3 0,2|

(1 0 0)* | 0 0,4 0,6| = (0,5 0,3 0,2);

| 0 0 1 |

К=2:

|0,5 0,3 0,2|

(0,5 0,3 0,2) * | 0 0,4 0,6| = (0,25 0,27 0,48);

| 0 0 1 |

К=3:

|0,5 0,3 0,2|

(0,25 0,27 0,48) * | 0 0,4 0,6| = (0,125 0,075+0,108 0,05+0,162+0,48) =

| 0 0 1 |

= (0,125 0,183 0,692)

Сигнальный граф:

S₁

S₂

S₃

Задание 4.

В аудиторскую фирму поступает простейший поток заявок на обслуживание с интенсивностью λ = 1,5 заявки в день. Время обслуживания распределено по показательному закону и равно в среднем трем дням. Аудиторская фирма располагает пятью независимыми бухгалтерами, выполняющими аудиторские проверки (обслуживание заявок). Очередь заявок не ограничена. Дисциплина очереди не регламентирована.

Определите вероятностные характеристики аудиторской фирмы как системы массового обслуживания, работающей в стационарном режиме.

Решение:

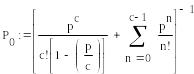
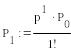
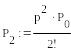
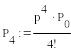
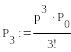
Задание 5. Необходимо принять решение в условиях неопределенности по матрице затрат с использованием различных критериев (Лапласа, Вальда, Сэвиджа, Гурвица).

	S1	S2	S3	S4
R1	6	12	20	24
R2	9	27	9	28
R3	23	18	15	19
R4	27	24	21	15

Решение:

1. Критерий Лапласа:

H(R1) = ¼ * (6+12+20+24) = 15,5;

H(R2) = ¼ * (9+27+9+28) = 18,25;

H(R3) = ¼ * (23+18+15+19) = 18,75;

H(R4) = ¼ * (27+24+21+15) = 21,75;

M = min{15,5; 18,25; 18,75; 21,75} = 15,5

Оптимальная стратегия - R1

2. Критерий Вальда:

	S1	S2	S3	S4	max	min
R1	6	12	20	24	24
R2	9	27	9	28	28
R3	23	18	15	19	23	23
R4	27	24	21	15	27

Оптимальная стратегия – R3

3. Критерий Сэвиджа:

Матрица рисков:

	S1	S2	S3	S4	max	min
R1	0	0	11	9	11	11
R2	3	15	0	13	15
R3	17	6	6	4	17
R4	21	12	12	0	21

Оптимальная стратегия – R1

4. Критерий Гурвица:

	S1	S2	S3	S4	0,5min	0,5 max	сумма	min
R1	6	12	20	24	3	12	15	15
R2	9	27	9	28	4,5	14	18,5
R3	23	18	15	19	7,5	11,5	19
R4	27	24	21	15	7,5	13,5	21

Оптимальная стратегия – R1