3. Обчислимо прогнозні значення Yпр:
У рівняння Yрозр = 23,89 +0,97X1 +0,38X2 підставимо прогнозні значення фактору Хпр = (1, 15, 35), що лежить за межами базового періоду (точковий прогноз):
Yпр = 23,89 + 0,97 15 + 0,38 35 = 51,79
Тоді M(Yпр) можна розглядати як оцінку прогнозного значення математичного сподівання та індивідуального значення обсягу виробленої продукції при відомих параметрах вартості основних засобів (Х1) та чисельності працюючих (Х2).
Визначимо
дисперсію прогнозу
з урахуванням матриці похибок, яка для
прикладу має вигляд:
(Х' Х)–1 = |
3,78969 |
0,12007 |
–0,20478 |
0,12007 |
0,03291 |
–0,01593 |
|
–0,20478 |
–0,01593 |
0,01438 |
Елементи дисперсійно-ковартційної матриці, які розраховуються за формулами і мають значення:
|
6,36573 |
0,20169 |
–0,343982 |
var (В) = |
0,20169 |
0,05529 |
–0,02676 |
|
–0,343982 |
–0,02676 |
0,02415 |
Хпр = |
1 |
15 |
|
35 |
Х'пр = |
1 |
15 |
35 |
Х'пр * var (В) = |
–2,6483 |
0,0944 |
0,0999 |
Знайдемо дисперсію прогнозу:
Середньоквадратична похибка прогнозу математичного сподівання M(Ynp):
Довірчий інтервал для математичного сподівання M(Ynp) прогнозного значення розрахуємо за формулою:
де t – табличне значення t-критерію Ст’юдента з ступенем вільності k=n–m1 та рівнем значимості =0,05.
51,79 – 2,57058 1,5046 ≤ M(Yпр) ≤ 51,79 + 2,57058 1,5046
47,9264 |
≤ M(Yпр) ≤ |
55,6617 |
Знайдемо межі інтервального прогнозу індивідуального значення Yпр:
Для цього обчислимо дисперсію та стандартну похибку прогнозу індивідуального значення Yпр:
51,79 – 2,57058 1,9858 ≤ Yпр ≤ 51,79 + 2,57058 1,9858
46,6893 |
≤ Yпр ≤ |
56,8988 |
4. Графічне зображення моделі ґрунтується на побудові ліній регресії, в прямокутних координатах Y – x1 та Y – x2 (рис. 6.1).
При цьому масштаб треба обрати таким, щоб мінімальні та максимальні значення x1 та x2 співпадали між собою.
Лінія регресії Y=f(X1) при X2=const відображає вплив першого фактора х1 на продуктивність праці при постійному значенні другого х2 (середнє значення х2).
Лінія регресії Y=f(X2) при X1=const відображає вплив другого фактора х2 на продуктивність праці при постійному значенні х1 (середнє значення х1).
|
X1 |
X2 |
Y=f(X1) при X2=const |
Y=f(X2) при X1=const |
Середні значення |
|
min |
4,20 |
13,00 |
30,64 |
35,64 |
X1 |
X2 |
max |
14,20 |
28,00 |
40,38 |
41,34 |
7,00 |
22 |
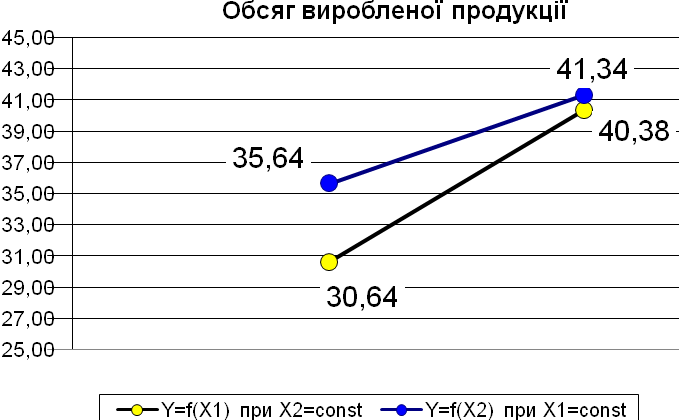
Рис. 6.1. Графічне зображення моделі