
Лабораторне заняття № 6 «Множинна лінійна кореляційна модель».
Згідно
з вибіркою статистичних даних за
роки дослідження (додаток 5), які
характеризують обсяг виробленої
продукції (Y), тис. т в залежності від
вартості основних засобів (Х1),
тис. грн. та чисельності працюючих (Х2),
чол. побудувати лінійну регресійну
модель виду
![]()
Потрібно: знайти параметри моделі; оцінити тісноту та значимість зв’язку між змінними моделі; проаналізувати достовірність моделі та її параметрів. Відобразити модель на графіку. Застосувати модель для прогнозування розвитку економічних процесів. Виконати економічний аналіз отриманих результатів.
У моделях множинної регресії розглядають множину даних по кожному зі змінних як вектор-стовпчик, а вільному членові відповідає вектор, що складається лише з одиниць.
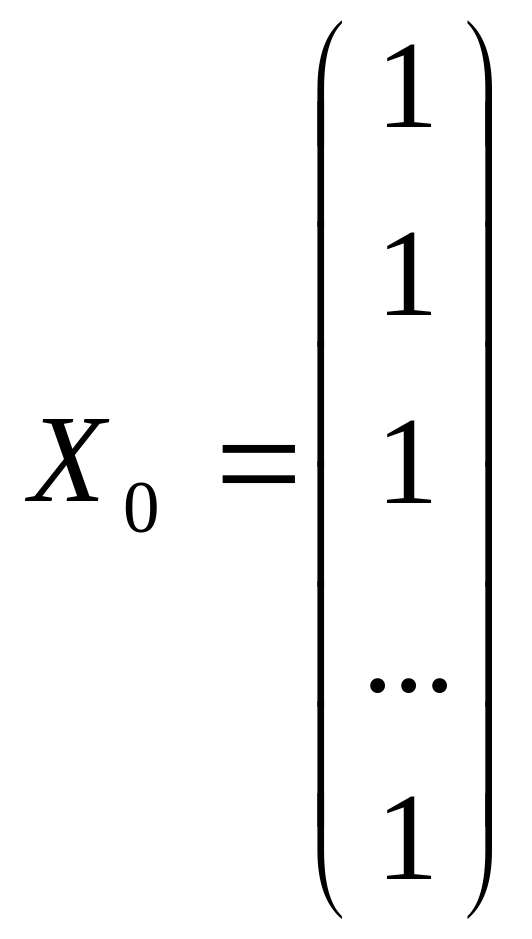
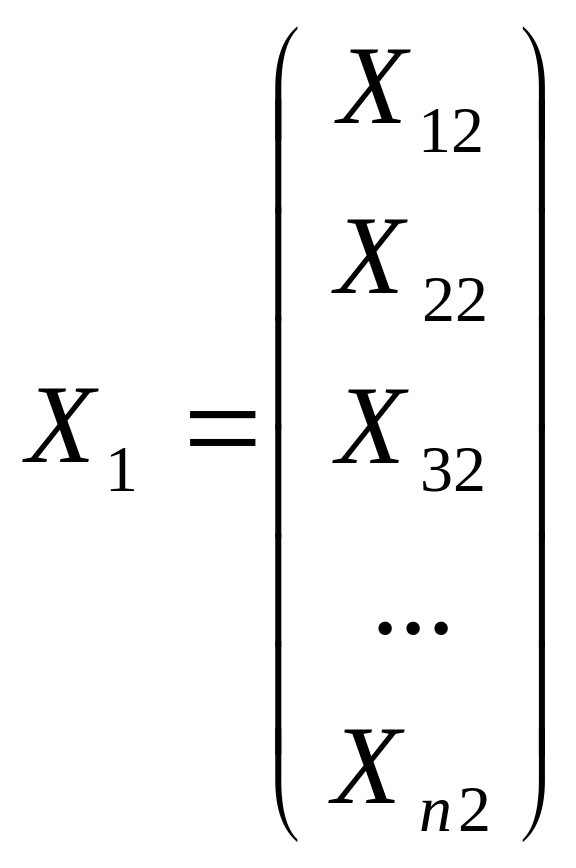
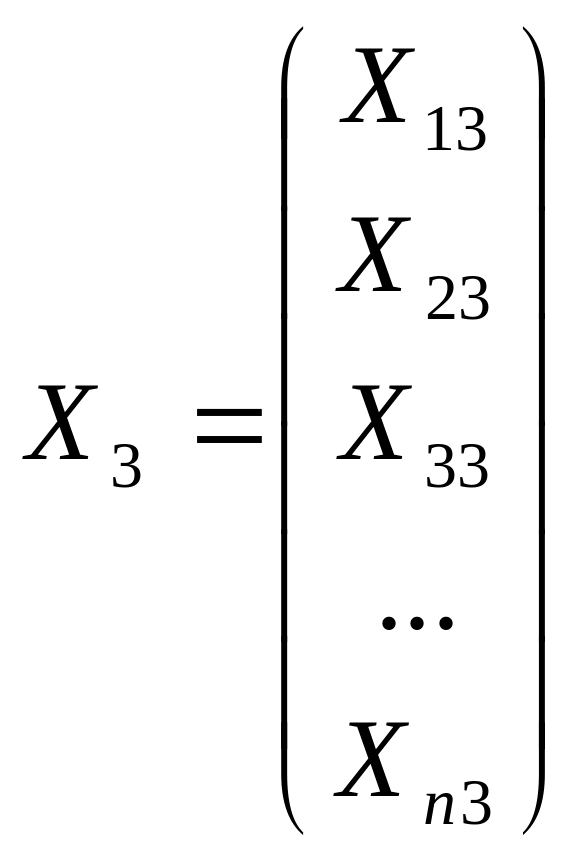
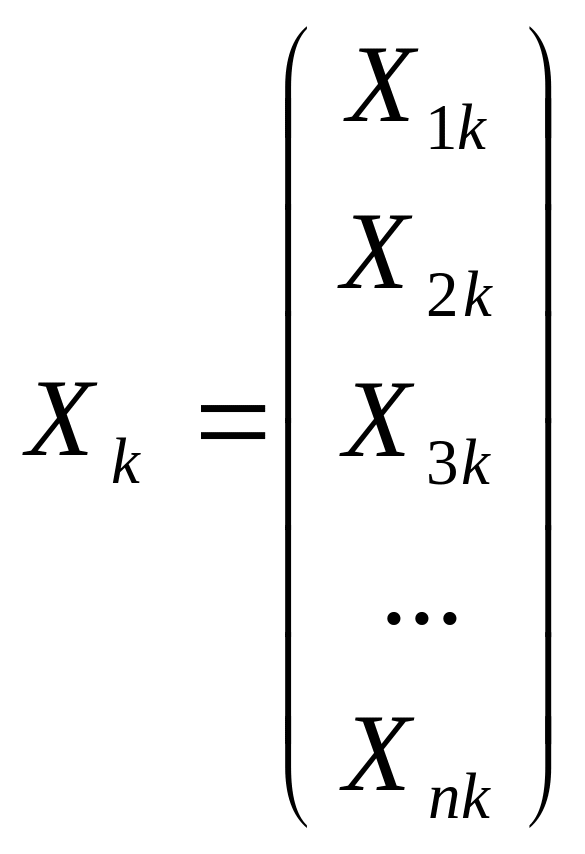
; ; ; . . . ; .
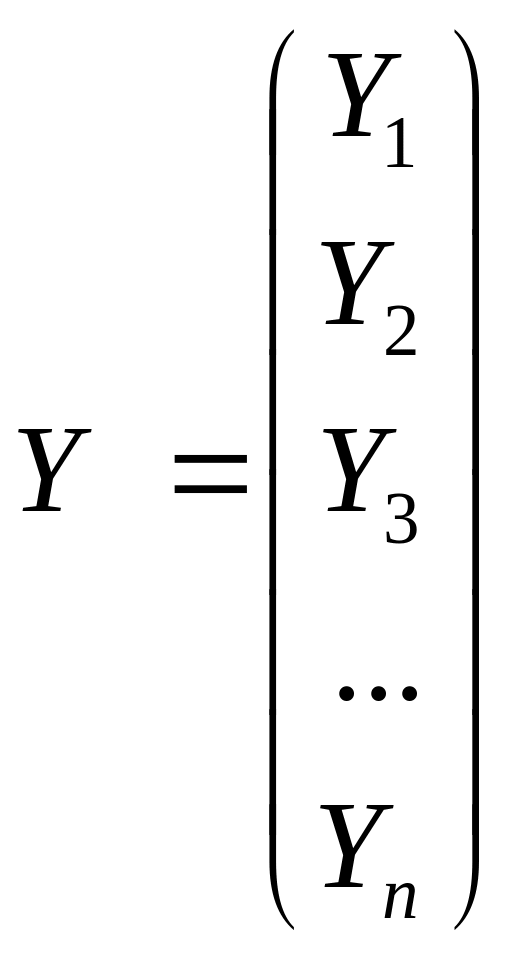
– вектор-стовпець залежної змінної.
– вектор параметрів.
Векторну оцінку параметрів теоретичної моделі (*) знаходять за методом найменших квадратів. Для цього треба виконати обчислення за формулою (6.1), яка в нашому випадку буде мати вигляд:
![]() (6.1)
(6.1)
Приклад виконання завдання
Задача. Згідно з вибіркою статистичних даних за 8 років, які характеризують обсяг виробленої продукції (Y), тис. т в залежності від вартості основних засобів (Х1), тис. грн. та чисельності працюючих (Х2), чол. побудувати лінійну регресійну модель виду:
Y =0 + 1 X1 + 2 X2.
Знайти векторну оцінку * за методом найменших квадратів, для цього треба виконати обчислення за формулою (6.1)
Проаналізувати достовірність моделі та її параметрів. Для аналізу необхідно розрахувати:
коефіцієнт детермінації;
скоригований коефіцієнт детермінації;
множинний коефіцієнт кореляції R;
парні коефіцієнти кореляції;
частинні коефіцієнти кореляції;
стандартні похибки оцінок параметрів моделі (порівняти з величиною оцінок);
перевірити значущість коефіцієнта детермінації, коефіцієнта кореляції та оцінок параметрів моделі множинної регресії;
знайти інтервали надійності для оцінок параметрів моделі.
Знайти прогнозні значення матриці залежних змінних Yпр, які відповідають очікуваним значенням матриці незалежних змінних Xпр.
Відобразити модель на графіку.
Зробити економічний висновок.
Вихідні дані для розрахунку в табл. 6.1.
Таблиця 6.1
Спостереження |
обсяг виробленої продукції, тис. т |
вартість основних засобів, тис. грн. |
чисельність працюючих, чол. |
|
Y |
Х1 |
Х2 |
1 |
33 |
4,2 |
13 |
2 |
36 |
5,3 |
18 |
3 |
37 |
6,5 |
24 |
4 |
38,2 |
5,8 |
22 |
5 |
38,5 |
6,9 |
22 |
6 |
40,2 |
5,9 |
24 |
7 |
41,1 |
7,2 |
25 |
8 |
48,5 |
14,2 |
28 |
Середні значення |
39,06 |
7,00 |
22 |
