
- •Билет 1
- •1) Классификация электронных элементов и цепей.
- •Классификация электрических цепей и их элементов
- •2) Спектр производной и интеграла функции. Основные свойства спектральных характеристик сигналов
- •Дифференцирование сигнала
- •Интегрирование сигнала
- •Билет 2
- •4.2 Преобразование спектров в нелинейных цепях.
- •5.2 Расчет спектра короткого импульса.
- •Билет 6
- •Билет 7
- •Преобразование спектров параметрической индуктивностью
- •Билет №8
- •Вопрос 1 получение и решение уравнений длинной линии для режима бегущих волн
- •Вопрос 2 преобразование спектров параметрической емкостью
- •Билет №9
- •Вопрос 1 линия в режиме стоячих волн.
- •Вопрос 2 амплитудная модуляция и демодуляция сигналов в радиосвязи.
- •2. Амплитудная модуляция
- •2.1. Однотональная ам
- •2.2. Ам с подавленной несущей
- •2.3. Однополосная модуляция
- •Свойства:
- •2.Тепловой шум: природа, свойства и методы борьбы с ним.
- •12.1. Каскады усиления с общим коллектором и общей базой: схемы, свойства и применение.
- •12.2. Дробовой шум: природа, свойства и методы его снижения.
- •Обратная связь в усилителях . Влияние отрицательной обратной связи на основные свойства усилителей.
- •Фликкерный ( 1/f) шум- свойства, источники.
- •14 Билет
- •Билет 18
- •Интегрирующая цепь rc
- •21.1 Интегральное преобразование Фурье (ипф)
- •21.2 Построение фильтров типа к. Анализ фнч
- •Стабилизированные источники питания и инверторные устройства
- •Фурье – преобразование для дискретизованного сигнала.
5.2 Расчет спектра короткого импульса.
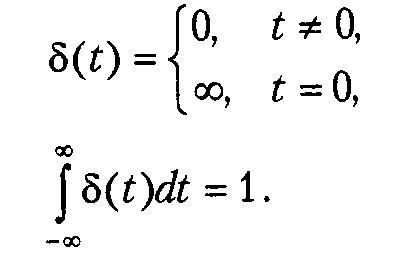 Короткий
импульс это кратковременный всплеск
напряжения или тока. Его можно представить
в виде функции Дирака.
Короткий
импульс это кратковременный всплеск
напряжения или тока. Его можно представить
в виде функции Дирака.
Она обладает фильтрующим свойством.
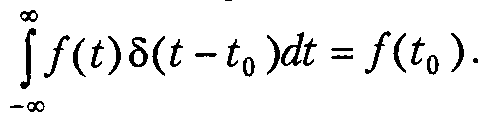
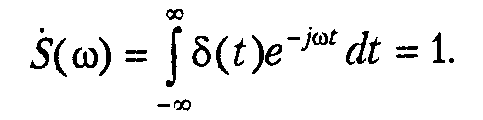 Если
воспользоваться преобразованием Фурье
и предыдущим свойством, то спектр
дельта-функции представляет собой
константу, то есть является равномерным
в бесконечной полосе частот.
Если
воспользоваться преобразованием Фурье
и предыдущим свойством, то спектр
дельта-функции представляет собой
константу, то есть является равномерным
в бесконечной полосе частот.
Билет 6
Параметры четырехполюсника можно задать различными параметрическими уравнениями.
Наибольшее распространение получили 6 систем уравнений:
G-параметры
h-параметры
Y-параметры
Z-параметры
A-параметры
B-параметры
соответственно уравнения будут:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
переход между коэффициентами систем уравнений h и Y:
![]()
![]()
![]()
![]()
Преобразование спектров с параметрической емкостью
Пусть проводимость задана следующим выражением
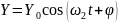
а напряжение задано гармоническим сигналом
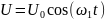
тогда ток будет определяться
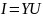
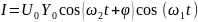
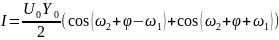
Следовательно в спектре появляется гармоники ω2 - ω1 и ω2 – ω1.
Билет 7
Характеристические (вторичные) параметры следующие:
Характеристические сопротивления
Постоянная передачи
ZC1 и ZC2 -это пара сопротивлений, такая, что при подключении к выходным зажимам сопротивления нагрузки ZH2 равного ZC2 (выходное характеристическое сопротивление), входное сопротивление четырехполюсника со стороны входных зажимов будет равно ZC1 (входное характеристическое сопротивление).
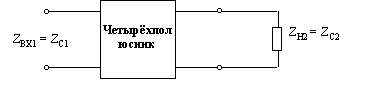
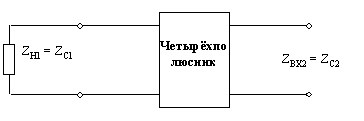
введем систему А-параметров
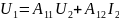
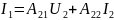
Вводя характеристические сопротивления
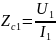
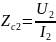
Можно расписать
![]()
![]()
Откуда
![]()
![]()
Если четырехполюсник симметричный A11=A22,то
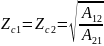
Характеристическая постоянная передачи
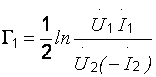
Если четырехполюсник симметричный то Г1=Г2=Г
Параметры сложных четырехполюсников
Любой сложный четырёхполюсник можно разбить на более простые с соответствующими соединениями.
1)Последовательное соединение. В этом случае Z-параметры общего четырехполюсника представлены суммой соответствующих параметров.
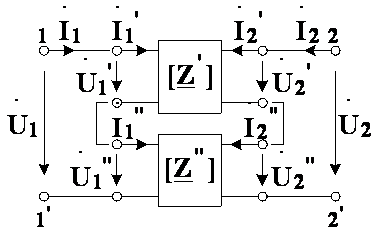
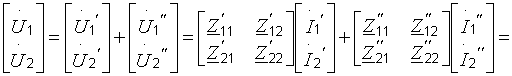
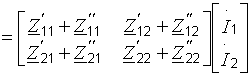
2)Параллельное соединение. Y-матрица общего четырехполюсника представлена суммой соответствующих матриц.
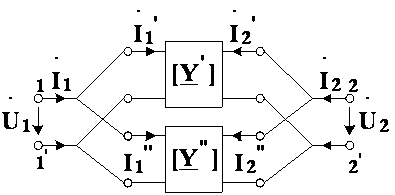
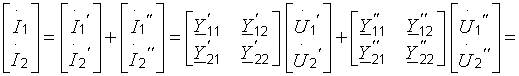
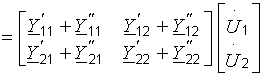
3)Последовательно параллельное. H-матрица общего четырехполюсника представлена суммой соответствующих матриц.
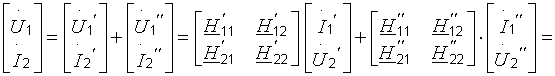
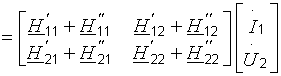
4)Каскадное соединение. А-матрица общего четырехполюсника представлена произведением соответствующих матриц
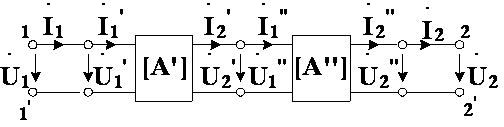
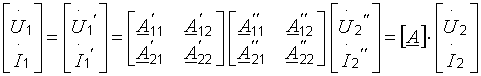
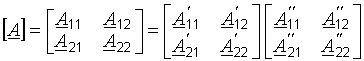
Преобразование спектров параметрической индуктивностью
Пусть проводимость индуктивности представлена следующим выражением
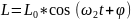
Напряжение будет задано гармоническим сигналом
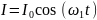
Тогда напряжение в цепи будет определяться выражением:
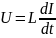
Следовательно
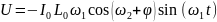
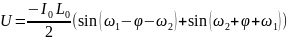
То есть в спектре сигнала появляются ω1-ω2 и ω2 – ω1 составляющие.
Билет №8
Вопрос 1 получение и решение уравнений длинной линии для режима бегущих волн
Длинная линия — регулярная линия электропередачи, длина которой превышает длину волны колебаний, распространяющихся в ней, а расстояние между проводниками, из которых она состоит, значительно меньше этой длины волны.
Характерной особенностью длинных линий является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается подключенным к линии генератором электромагнитных колебаний, и называется падающей. Другая волна называется отражённой, и возникает из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.
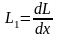
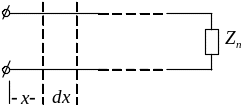 -
погонная индуктивность
-
погонная индуктивность
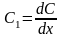 -
погонная емкость
-
погонная емкость
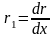
![]() -
погонное сопротивление
-
погонное сопротивление
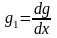 -
погонная проводимость
-
погонная проводимость
Уравнения
линии:
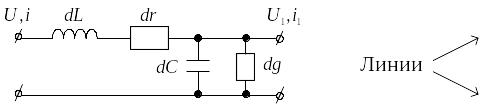
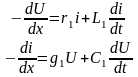
Телеграфные уравнения (определяют связь между током и напряжением в любом сечении линии):
Решение уравнений для линии без потерь (
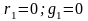 )
)
 I
I
Решениями этих уравнений являются волны тока и напряжения, т.е.:
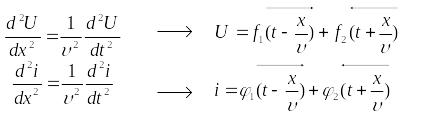
2. Решение телеграфных уравнений для линии с потерями.
П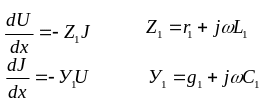 усть
усть
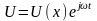
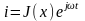
Тогда телеграфные уравнения примут вид:
![]()
![]()
Продифференцируем
по x:

Решение
первого уравнения:
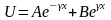 ,
,
где
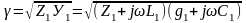 называется
постоянной распространения.
называется
постоянной распространения.
Для
тока из второго уравнения:
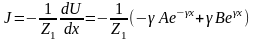
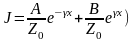 ,
где
,
где
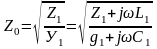 - волновое сопротивление линии.
- волновое сопротивление линии.
3. Учет граничных условий.
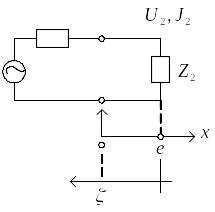
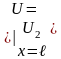

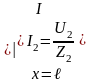
Находим
А, В:
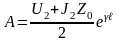
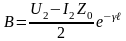
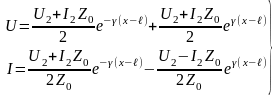
Коэффициент
отражения:
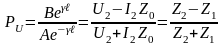
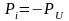
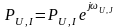
Сделаем
замену:
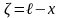
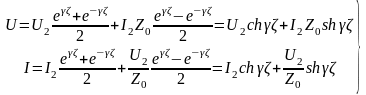
Входное
сопротивление линии
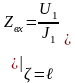
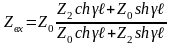 через
через
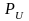
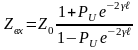
В
режиме бегущих
волн:
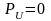 при
при
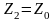 и
и
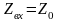 ,
т.е. не зависит от длины линии, всё
поглощается в нагрузку.
,
т.е. не зависит от длины линии, всё
поглощается в нагрузку.
