
- •Билет 1
- •1) Классификация электронных элементов и цепей.
- •Классификация электрических цепей и их элементов
- •2) Спектр производной и интеграла функции. Основные свойства спектральных характеристик сигналов
- •Дифференцирование сигнала
- •Интегрирование сигнала
- •Билет 2
- •4.2 Преобразование спектров в нелинейных цепях.
- •5.2 Расчет спектра короткого импульса.
- •Билет 6
- •Билет 7
- •Преобразование спектров параметрической индуктивностью
- •Билет №8
- •Вопрос 1 получение и решение уравнений длинной линии для режима бегущих волн
- •Вопрос 2 преобразование спектров параметрической емкостью
- •Билет №9
- •Вопрос 1 линия в режиме стоячих волн.
- •Вопрос 2 амплитудная модуляция и демодуляция сигналов в радиосвязи.
- •2. Амплитудная модуляция
- •2.1. Однотональная ам
- •2.2. Ам с подавленной несущей
- •2.3. Однополосная модуляция
- •Свойства:
- •2.Тепловой шум: природа, свойства и методы борьбы с ним.
- •12.1. Каскады усиления с общим коллектором и общей базой: схемы, свойства и применение.
- •12.2. Дробовой шум: природа, свойства и методы его снижения.
- •Обратная связь в усилителях . Влияние отрицательной обратной связи на основные свойства усилителей.
- •Фликкерный ( 1/f) шум- свойства, источники.
- •14 Билет
- •Билет 18
- •Интегрирующая цепь rc
- •21.1 Интегральное преобразование Фурье (ипф)
- •21.2 Построение фильтров типа к. Анализ фнч
- •Стабилизированные источники питания и инверторные устройства
- •Фурье – преобразование для дискретизованного сигнала.
Дифференцирование сигнала
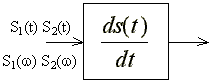
|
,
|
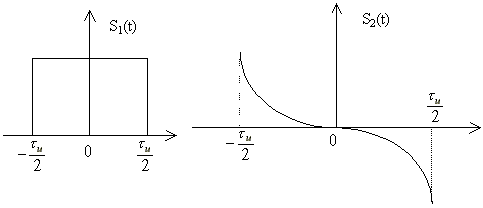
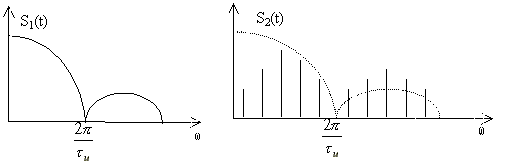
Интегрирование сигнала
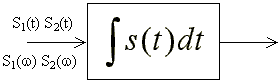
|
, |
|
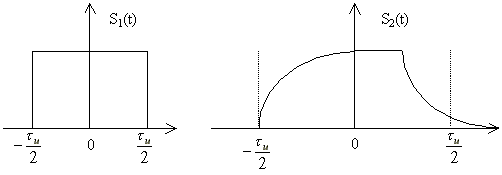
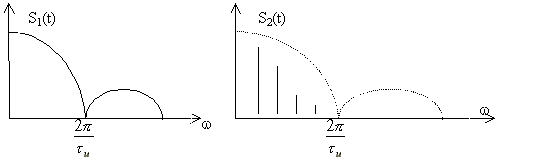
Билет 2
2.1





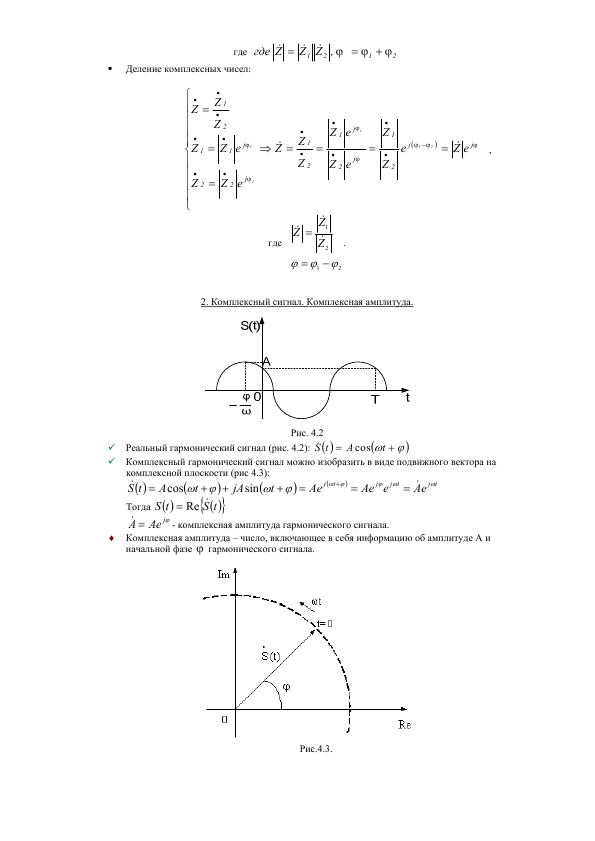


2.2 Спектр суммы функций и сдвинутой функции.
Спектр суммы равен сумме спектра. Это ясно и ежу. Из-за линейности всех этих вещей. И сдвинутой функции – сдвинутая домножается на экспоненту, сдвиг функции по времени на модуль не оказывает влияния, меняет только их фазовые составляющие: пример с прямоугольными импульсами и куча фазовых функций. Берем снимок мгновенный в моменты времени, как удачно выбираем момент времени, чтоб сделать сечение по всем частотам, так и будет простой или сложный спектр. Поэтому так и определяем.
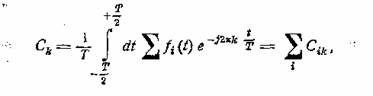
Билет 3
3.1 Единство частотного и временного описаний для лин. Цепей
Используем временное описание, когда работа цепи в переходной режиме: было в одном стационарном состоянии, вот переходит в другое стационарное состояние. Развитие в процессе во времени и суть вопроса, который нас интересует. Используем временной подход. Пример – дифференцирующая цепочка. На вход подается прямоугольный импульс, на выходе будет остроконечный импульс, характерный для дифференцирующей цепочки. Оцениваем, выдвигаем гипотезы. Переходим к частот описанию, комплексное пространство в режиме стационарном рассматривается, находим коэффициент передачи. На низких частотах маленький коэффициент, с ростом частоты возрастает. Как в ФВЧ. Сравниваем временной отклик и форму частот. Быстроперемен часть сигнала, фронт, описывается в основном высокочастатотными составляющими спектра. Они хорошо переданы, сохраняются. У вершины оно упало. Низкочастототные компоненты плохо передаются, частот характеристики они заваливаются. Мы находим частичные суммы гармоник, это влияет – с ростом добавленных гармоник частот, растет фронт, увел крутизна у него. Если выбросить низкочастные компоненты, то начнет резко деформироваться вершина, медленная часть сигнала. Окончательная суммируя – присутствие в спектре сигнала высокочастотных компонент, приводит к тому, что в виде сигнала во временном пространстве будем наблюдать быстропеременные части с большими производными, а низкочастотные ответственны за точность передачи медленной части сигнала.


3.2 Ряд Котельникова для спектральной функции
Сформулировать – для временной функции знаем, функция определена полностью своими выборками дважды за период самой высокой частоты. А если этот же подход применить к спектр функции, то можно всю спек функцию не передавать, а взять только выборки, но будет тот же самый эффект – не потеряем инфы об этом спектре, об этом процессе.

Дальше в учебнике приводятся сплошные формулы, они не нужны.
4.2 Преобразование спектров в нелинейных цепях.
В
нелинейных системах связь между входным
сигналом
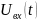 и выходной реакцией
и выходной реакцией
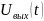 устанавливается нелинейной функциональной
зависимостью
устанавливается нелинейной функциональной
зависимостью
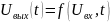
Будем
рассматривать внешние характеристики
нелинейных двухполюсников, когда входным
сигналом служит напряжение
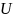 ,
а выходным — ток
,
а выходным — ток
 .
Зависимость
.
Зависимость
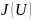 принято называть вольт-амперной
характеристикой (ВАХ) нелинейного
элемента.
принято называть вольт-амперной
характеристикой (ВАХ) нелинейного
элемента.
П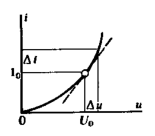 онятие
сопротивление для линейного двухполюсника
можно определить по-разному. Приложив
к двухполюснику постоянное напряжение
онятие
сопротивление для линейного двухполюсника
можно определить по-разному. Приложив
к двухполюснику постоянное напряжение
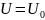 ,
получим цепи ток
,
получим цепи ток
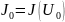 .
Отношение
.
Отношение
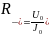 называют сопротивление элемента
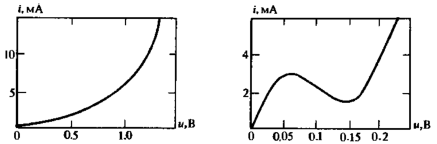
постоянному току. Отношение приращения
напряжения к приращению тока в выбранной
рабочей точке
называют сопротивление элемента
постоянному току. Отношение приращения
напряжения к приращению тока в выбранной
рабочей точке
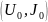 называют дифференциальным сопротивлением
нелинейного двухполюсника:
называют дифференциальным сопротивлением
нелинейного двухполюсника:
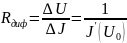 или дифференциальной крутизной ВАХ:
или дифференциальной крутизной ВАХ:
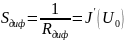 .
.
Рассмотрим
последовательность соединения источника
сигнала
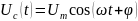 ,
источника постоянного напряжения
смещения
,
источника постоянного напряжения
смещения
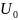 и нелинейного элемента с ВАХ
и нелинейного элемента с ВАХ
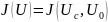 .
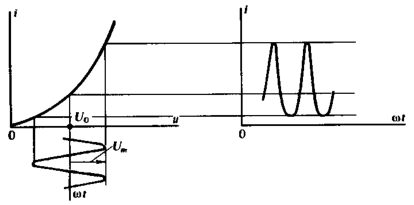
На рисунке ниже показано, как нелинейный
элемент искажает сигнал.
.
На рисунке ниже показано, как нелинейный
элемент искажает сигнал.
Пусть
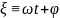 .
Тогда функция
.
Тогда функция
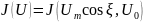 оказывает периодичной относительно
аргумента
оказывает периодичной относительно
аргумента
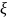 с периодом
с периодом
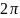 ,
поэтому её можно разложить в ряд Фурье:
,
поэтому её можно разложить в ряд Фурье:
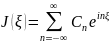
Где
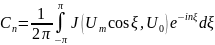
Так
как
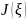 чётная, то ряд Фурье можно упростить:
чётная, то ряд Фурье можно упростить:
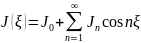
Где
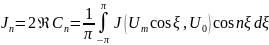
Таким
образом, из простого гармонического
сигнала с частотой
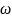 получился сигнал с гармониками
получился сигнал с гармониками
 .
.
