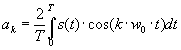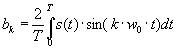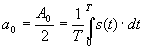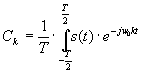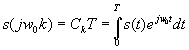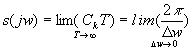2) Спектр производной и интеграла функции. Основные свойства спектральных характеристик сигналов

Фурье-изображения — комплексные коэффициенты ряда Фурье F(j_k) периодического сигнала (1) и спектральная плотность F(j) непериодического сигнала (2) — обладают рядом общих свойств.

1. Линейность. Интегралы (1) и (2) осуществляют линейное преобразование функции f(t). Поэтому Фурье-изображение линейной комбинации функций равно аналогичной линейной комбинации их изображений. Если f(t) = a₁f₁(t) + a₂f₂(t), то F(j) = a₁F₁(j) + a₂F₂(j), где F₁(j) и F₂(j) — Фурье-изображения сигналов f₁(t) и f₂(t), соответственно.

2. Задержка (изменение начала отсчета времени для периодических функций). Рассмотрим сигнал f₂(t), задержанный на время t₀ относительно сигнала f₁(t), имеющего такую же форму: f₂(t) = f₁(t – t₀). Если сигнал f₁ имеет изображение F₁(j), то Фурье-изображение сигнала f₂ равно F₂(j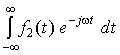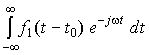) = = . Домножив и разделив на , сгруппируем члены следующим образом:

.

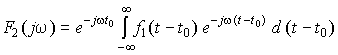Поскольку последний интеграл равен F₁(j), то F₂(j) = e^jt0 F₁(j). Таким образом, при задержке сигнала на время t₀ (изменении начала отсчета времени) модуль его спектральной плотности не изменяется, а аргумент уменьшается на величину t₀, пропорциональную времени задержки. Поэтому амплитуды спектра сигнала не зависят от начала отсчета, а начальные фазы при задержке на t₀ уменьшаются на t₀.

3. Симметрия. Для действительного f(t) изображение F(j) обладает сопряженной симметрией: F(– j) = . Если f(t) — четная функция, то Im F(j) = 0; для нечетной функции Re F(j) = 0. Модуль |F(j)| и вещественная часть Re F(j) — четные функции частоты, аргумент arg F(j) и Im F(j) — нечетные.

4. Дифференцирование. Из формулы прямого преобразования, интегрируя по частям, получим связь изображения производной сигнала f(t) с изображением самого сигнала

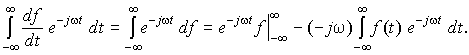
Для абсолютно интегрируемой функции f(t) внеинтегральный член равен нулю, и, следовательно, при , а последний интеграл представляет Фурье-изображение исходного сигнала F(j). Поэтому Фурье-изображение производной df/dt связано с изображением самого сигнала соотношением jF(j) — при дифференцировании сигнала его Фурье-изображение умножается на j. Это же соотношение справедливо и для коэффициентов F(j_k), которые определяются интегрированием в конечных пределах от – T/2 до + T/2. Действительно, произведение в соответствующих пределах

Поскольку вследствие периодичности функции f(T/2) = f(– T/2), а = = = (– 1)^k, то и в этом случае внеинтегральный член пропадает, и справедлива формула

где стрелкой символически обозначена операция прямого преобразования Фурье. Это соотношение обобщается и на многократное дифференцирование: для n-й производной имеем: dⁿf/dtⁿ (j)ⁿF(j). 

Полученные формулы позволяют найти Фурье-изображение производных функции по ее известному спектру. Эти формулы удобно также применять в случаях, когда в результате дифференцирования приходим к функции, Фурье-изображение которой вычисляется более просто. Так, если f(t) — кусочно-линейная функция, то ее производная df/dt — кусочно-постоянная, и для нее интеграл прямого преобразования находится элементарно. Для получения спектральных характеристик интеграла  функции f(t) ее изображение следует разделить на j.

5. Дуальность времени и частоты. Сопоставление интегралов прямого и обратного преобразований Фурье приводит к выводу о их своеобразной симметрии, которая становится более очевидной, если формулу обратного преобразования переписать, перенося множитель 2 в левую часть равенства:

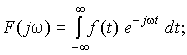
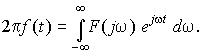
Для сигнала f(t), являющегося четной функцией времени f(– t) = f(t), когда спектральная плотность F(j) — вещественная величина F(j) = F(), оба интеграла можно переписать в тригонометрической форме косинус-преобразования Фурье:

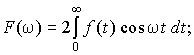
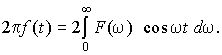
При взаимной замене t и  интегралы прямого и обратного преобразований переходят друг в друга. Отсюда следует, что если F() представляет спектральную плотность четной функции времени f(t), то функция 2f() является спектральной плотностью сигнала F(t). Для нечетных функций f(t) [f(t) = – f(t)] спектральная плотность F(j) чисто мнимая [F(j) = jF()]. Интегралы Фурье в этом случае приводятся к виду синус-преобразований, из которых следует, что если спектральная плотность jF() соответствует нечетной функции f(t), то величина j2f() представляет спектральную плотность сигнала F(t). Таким образом, графики временной зависимости сигналов указанных классов и его спектральной плотности дуальны друг другу.

Интеграл (1)

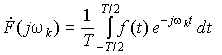
Интеграл (2)

В радиотехнике широко используется спектральное и временное представление сигналов. Хотя сигналы по своей природе являются случайными процессами, однако, отдельные реализации случайного процесса и некоторые специальные (например, измерительные) сигналы можно считать детерминированными (то есть известными) функциями. Последние принято делить на периодические и непериодические, хотя строго периодических сигналов не существует. Сигнал называется периодическим, если он удовлетворяет условию

. (1)

на интервале времени ,где Т - постоянная величина, называемая периодом, а k-любое целое число.

Простейшим примером периодического сигнала является гармоническое колебание (или коротко гармоника).

где - амплитуда, = - частота, - круговая частота, - начальная фаза гармоники.

Важное значение понятия гармоники для теории и практики радиотехники объясняется рядом причин:

1. гармонические сигналы сохраняют свою форму и частоту при прохождении через стационарные линейные электрические цепи (например, фильтры), меняя лишь амплитуду и фазу;

2. гармонические сигналы достаточно просто вырабатываются (например, при помощи автогенераторов LC).

Непериодическим сигналом называется сигнал, который отличен от нуля на конечном интервале времени. Непериодический сигнал можно рассматривать как периодический, но с бесконечно большим периодом. Одной из основных характеристик непериодического сигнала является его спектр. Спектром сигнала называют функцию, показывающую зависимость интенсивности различных гармоник в составе сигнала, от частоты этих гармоник. Спектр периодического сигнала - это зависимость коэффициентов ряда Фурье от частоты гармоник, которым эти коэффициенты соответствуют. Для непериодического сигнала спектр - это прямое преобразование Фурье сигнала. Итак, спектр периодического сигнала - это дискретный спектр (дискретная функция частоты), в то время как для непериодического сигнала характерен сплошной спектр (непрерывный) спектр.

Обратим внимание на то, что дискретный и непрерывный спектры имеют разные размерности. Дискретный спектр имеет ту же размерность, что и сигнал, в то время как размерность непрерывного спектра равна отношению размерности сигнала к размерности частоты. Если, например, сигнал представлен электрическим напряжением, то дискретный спектр будет измеряться в вольтах [B], а непрерывный - в вольт на герц [ B/Гц]. Поэтому для непрерывного спектра употребляют также термин "спектральная плотность".

Рассмотрим сначала спектральное представление периодических сигналов. Из курса математики известно, что любую периодическую функцию, удовлетворяющую условиям Дирихле (одним из необходимых является условие, чтобы энергия была конечной), можно представить рядом Фурье в тригонометрической форме:

(3)

(4)

(5)

где определяет среднее значение сигнала за период и называется постоянной составляющей. Частота называется основной частотой сигнала (частота первой гармоники), а кратные ей частоты - высшими гармониками. Выражение (3) можно представить в виде:

(6)

где

и

.(7)

Обратные зависимости для коэффициентов а и b имеют вид

и

(8)

На рисунке 1 приведен типичный вид графика спектра амплитуд периодического сигнала для тригонометрической формы ряда (6):

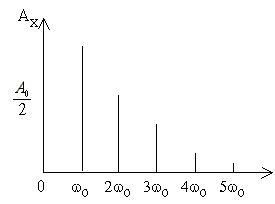
Рис.1

С использованием выражения (формула Эйлера).

вместо (6) можно записать комплексную форму ряда Фурье:

(9)

где коэффициент называются комплексными амплитудами гармоник, значения которых, как следует из (4) и формулы Эйлера, определяется выражением:

(10)

Сравнивая (6) и (9), замечаем, что при использовании комплексной формы записи ряда Фурье отрицательные значения k позволяют говорить о составляющих с "отрицательными частотами". Однако, появление отрицательных частот имеет формальный характер и связано с использованием комплексной формы записи для представления действительного сигнала.

Рассмотрим теперь спектр непериодического сигнала. Для этого обобщим формулу разложения в ряд Фурье (9) на случай, когда период Т стремиться к бесконечности. Как нетрудно заметить, при этом непериодическую функцию можно считать периодической. При увеличении Т частота первой гармоники

уменьшается и спектральные линии на рис.1 располагаются чаще. В пределе, при

,

интервал между линиями в спектре сокращается до нуля, т.е. спектр вместо дискретного становится сплошным, непрерывным. Амплитуды гармоник , согласно (10), становятся бесконечно малыми. Математически это можно выразить следующим образом. Введем вместо (10) функцию:

(11)

Тогда вместо (9) получим:

.(12)

 

При частота может принимать любое "текущее" значение w, а -w переходит в дифференциал dw и переходит в . Поэтому вместо (11) и (12) окончательно получим:

		(13)
		(14)

Эти выражения называются преобразованиями Фурье, которые связывают между собой функцию времени s(t) и комплексную функцию S(jw) в частотной области.

Физический смысл формулы (14) состоит в том, что непрерывный сигнал s(t) имеет непрерывный спектр, т.е. представляется бесконечной непрерывной суммой (интегралом) гармонических колебаний с бесконечно малыми комплексными амплитудами:

Функция

(15)

имеет размерность [амплитуда/герц] и показывает амплитуду сигнала, приходящуюся на полосу в 1 Герц. Поэтому эта непрерывная функция частоты S(jw) называется спектральной плотностью комплексных амплитуд или просто спектральной плотностью. Отметим одно важное обстоятельство. Сравнивая выражения (10) и (11) замечаем, что при w=kwo они отличаются лишь постоянным множителем, а

(16)

т.е. комплексные амплитуды периодической функции с периодом Т можно определить по спектральной характеристике непериодической функции такой же формы, заданной в интервале [0,Т]. Сказанное справедливо и по отношению к модулю спектральной плотности:

(17)

Из этого соотношения следует, что огибающая сплошного амплитудного спектра непериодического сигнала и огибающая амплитуд линейчатого спектра периодического сигнала совпадают по форме и отличаются лишь масштабом. Вычислим теперь энергию непериодического сигнала. Умножая обе части неравенства (14) на s(t) и интегрируя в бесконечных пределах, получим:

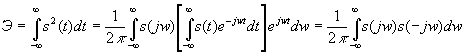
где S(jw) и S(-jw) - комплексно-сопряженные величины. Так как

то

(18)

Это выражение называется равенством Парсеваля для непериодического сигнала. Оно определяет полную энергию сигнала. Отсюда следует, что есть не что иное, как энергия сигнала, приходящаяся на 1 Гц полосы частот около частоты w. Поэтому функцию иногда называют спектральной плотностью энергии сигнала s(t). Приведем теперь без доказательства несколько теорем о спектрах, выражающих основные свойства преобразования Фурье.