Билет 18

Принцип усиления и генерирования сигналов на СВЧ.

При высоких частотах обычные усилители непригодны. Для генерирования и усиления сигналов на СВЧ применяют клистроны , магнетроны и лампы бегущей волны.

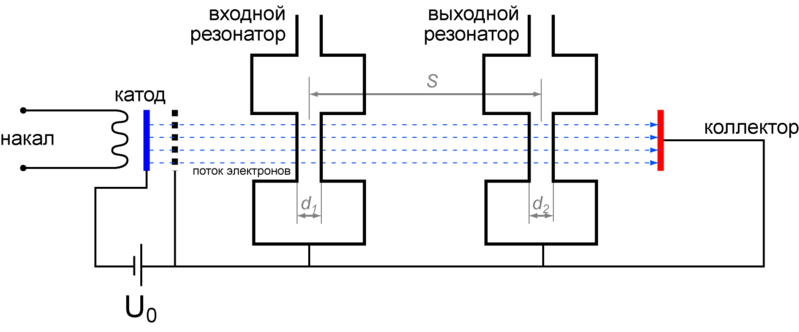
Клистрон

Φ- фокусирующая система (группирователь)

   Одной из Частей клистрона, как и любой радиолампы, является катод. Здесь берет свое начало поток быстро летящих электронов. Особое устройство «стягивает» их в узкий пучок и направляет вдоль оси баллона к собирательному электроду, имеющему высокое положительное напряжение.

   Все электроны на первом участке своего пути летят примерно с одинаковой скоростью, образуя на этом участке непрерывный однородный поток. Но вот они попадают в пространство между двумя сетками, расположенными очень близко одна к другой, и в движении их наступает резкая перемена.

   Сетки являются противоположными стенками полого резонатора, к которому подводятся электромагнитные колебания. В пространстве между сетками создается электрическое поле, действующее на электроны.

   Сила этого поля очень часто меняет свое направление. В некоторый момент времени она действует подобно встречному ветру и тормозит движение электронов. Затем действие ее прекращается, так как поле исчезает. Потом поле появляется вновь, но сила его действует уже в обратную сторону, подгоняя электроны, подобно попутному ветру, и движение их ускоряется. Такое вмешательство ведет к перестройке электронного потока, необходимой для возбуждения сверхбыстрых колебаний. Проследим внимательнее, как это происходит.

   Переменное электрическое поле, созданное на пути электронов, заставляет их двигаться с разными скоростями. Те электроны, которые пролетели между сетками резонатора при тормозящем поле, потеряли часть своей скорости и стали перемещаться медленнее, чем раньше. Электроны, пролетевшие сквозь сетки чуть-чуть позже, не испытали влияния электрического поля и продолжают полет с прежней скоростью. Электроны, пролетевшие между сетками еще позже при ускоряющем поле, получили дополнительный разгон и движутся теперь с большей скоростью.

   Вылетая за пределы резонатора, электроны попадают в пространство, где переменное электрическое поле уже не действует и где скорости их не меняются.

   Раньше всех там появляются замедленные электроны, которые движутся впереди. За ними следуют электроны, скорость которых не изменилась, и наконец несколько позади — электроны, получившие ускорение. Расстояния, разделяющие их, стремительно сокращаются. Электроны, летящие со средней скоростью, догоняют передних, а самые быстрые, летящие сзади, настигают и тех, и других.

   На некотором расстоянии от резонатора отдельные электроны собираются в ’группу большой плотности, перед которой создается разрежение. Группирование электронов идет непрерывно. Не успеет один электронный сгусток покинуть это место, как здесь появляется новый. Так равномерный поток электронов превращается в отдельные электронные сгустки, способные отдавать энергию сильными импульсами — толчками.

   Как раз там, где создается наибольшее сгущение, для улавливания этой энергии помещают второй полый резонатор. Две его противоположные стенки с отверстиями образуют вторую пару сеток, поставленную на пути летящих электронов. Пересекая пространство между этими сетками, электроны отдают здесь свою энергию. Электронный «прибой» действует на резонатор, и в нем возникают мощные электромагнитные колебания, которые при помощи металлической петли, вставленной в резонатор через небольшое отверстие, отводятся для использования.

   За пределами второго резонатора группировка электронов уже не сохраняется. Там электроны попадают на собирательный положительно заряженный электрод - коллектор.

   Чем же интересны колебания, возникающие во втором резонаторе? По частоте они совпадают с колебаниями первого резонатора, который производит группирование электронов, но мощность их в несколько раз больше. Таким образом, клистрон может работать как усилитель колебаний, подводимых к первому резонатору. Если же второй резонатор электрически соединить с первым, то это соединение будет выполнять роль, подобную обратной связи в обычном ламповом генераторе, - клистрон сам превратится в источник сверхбыстрых колебаний. Когда клистрон подключается к источникам электропитания, неизбежно возникает электрический «толчок», вызывающий собственные колебания в резонаторах. Благодаря обратной связи некоторая доля энергии колебаний второго резонатора попадает в первый и вызывает группирование электронов. В результате энергия электронного «прибоя» будет поддерживать колебания второго резонатора, не давая им затухнуть.

   Клистроны малой мощности делаются с одним резонатором, который одновременно и группирует электроны, и улавливает их энергию. Такие клистроны проще настраиваются и используются преимущественно для создания вспомогательных колебаний в приемниках сантиметровых волн.

клистроны являются основой всех мощных СВЧ передатчиков когерентных радиосистем, где реализуется стабильность и спектральная частота высокостабильных водородных стандартов частоты. 

Источник: Ф. Честнов - "В мире радио", 1954г.

Минус

Взаимодействие электронного луча управ-м сигналом и отдача энергии сгруппированным лучом выходному устройству происходит ограниченное время в узком зазоре между сетками.

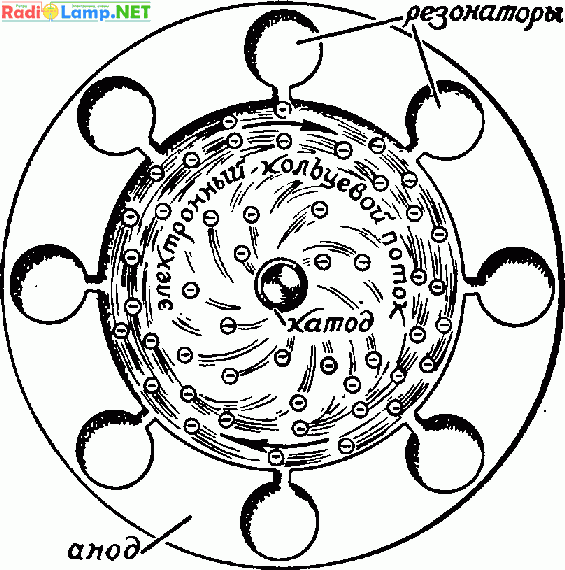
Магнетрон

Другой источник сверхбыстрых колебаний - магнетронный генератор. Были разработаны лампы, в которых на электронный поток одновременно действуют электрическое и магнитное поля. Такие лампы называются магнетронами.

Магнетрон имеет всего два электрода: анод - цилиндрической формы и прямолинейный катод, совпадающий с осью анода. Магнетрон находится между полюсами сильного магнита и расположен так, что силовые линии магнитного поля пронизывают внутреннее пространство вдоль оси анода.

Когда электроны покидают катод, они попадают в сферу действия электрического поля анода и поля магнита. Сила электрического поля влечет электроны к аноду, и они устремляются туда по самым коротким путям - по радиусам. Им приходится пересекать силовые линии магнитного поля. При этом на электроны начинает действовать новая сила, которая отклоняет их в сторону. Она искривляет путь электронов, «закручивая» их вокруг магнитных силовых линий.

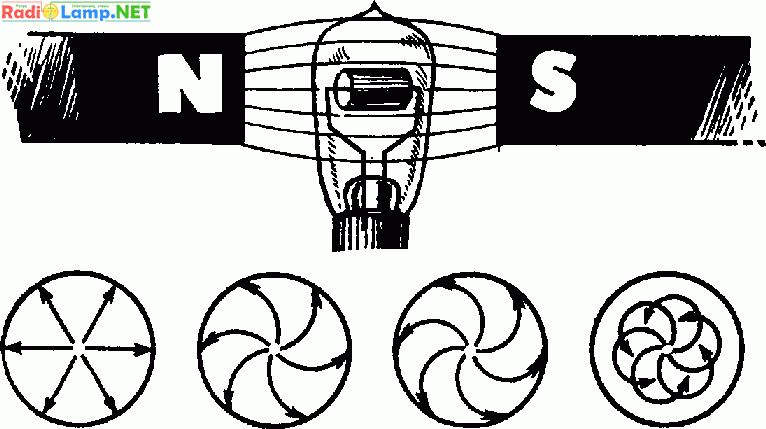
Влияние магнитного поля на движение электронов в магнетроне; по мере усиления магнитного поля траектории электронов все более и более искривляются

Влияние слабого магнитного поля на полет электронов еле заметно: их пути до анода остаются почти прямолинейными. Сильное же магнитное поле заставляет электроны лететь по кривым линиям. При определенных условиях электроны не станут попадать на анод, т. е., не долетая до него, будут возвращаться на катод; при этом анодный ток прекратится.

Анодное напряжение и силу магнитного поля подбирают так, что поворот электронов происходит у самой поверхности анода.

Электроны летят к аноду непрерывным потоком. На место тех, которые повертывают обратно, появляются новые. В результате вблизи анода возникает своего рода электронное облачко. Все электроны этого облачка, подчиняясь действию магнитного поля, движутся в одну и ту же сторону и образуют непрерывный кольцевой поток. Его нетрудно «подтянуть» почти вплотную к аноду, регулируя анодное напряжение.

Если к магнетрону подключить колебательный контур, то получится схема генератора, способного создавать незатухающие колебания.

Малейший электрический «толчок» в схеме нарушает равнове-сие и вызывает пульсации электронного потока. Так как этот поток почти касается поверхности анода, электроны начинают попадать на анод. В анодной цепи возникают импульсы тока, которые создают колебания в контуре.

 

Обычно магнетрон этого типа имеет четное число резонаторов: 8, 10, 12 и т. д. Это цилиндрические продольные полости, расположенные по кругу. Они сообщаются с центральной полостью, где помещен катод, узкими продольными щелями. Таким образом, поперечное сечение каждой резонаторной камеры напоминает по виду подкову.

Для получения сильных токов катод магнетрону делают больших размеров. Он испускает во всех радиальных направлениях мощный поток электронов.

При любом электрическом «толчке» в схеме (например, при ее подключении к источникам электропитания) в резонаторах магнетрона возникают колебания. В результате возле щелей, где движется электронное облачко, будет действовать переменное электрическое поле.

Электронные сгустки располагаются вокруг катода подобно спицам в колесе. Это электронное «колесо» быстро вращается. Пролетая мимо резонаторных щелей последовательно друг за другом, сгустки электронов сообщают резонаторам мощные электрические «толчки» и тем самым поддерживают возникшие в них колебания.

Отдавая свою энергию резонаторам, электроны в конце концов попадают на анод, но с катода прибывают все новые и новые порции электронов, и поэтому электронное облачко не пропадает. В магнетроне устанавливаются незатухающие колебания сверхвысокой частоты.

Резонаторные полости связаны между собой короткими металлическими перемычками - связками и составляют единую колебательную систему. Частота возбуждаемых колебаний определяется размерами резонаторов. Для вывода энергии этих колебаний служит специальный отвод в виде небольшой металлической петли, помещенной в одной из резонаторных полостей.

Магнетрон способен создавать колебания, обеспечивающие получение волн до одного сантиметра длиной и даже короче. Он незаменим в радиопередатчиках, работа которых требует колебаний большой мощности, и может успешно работать в импульсном режиме (генерировать кратковременные импульсы). Благодаря этому магнетрон получил широкое применение в технике ультракоротких волн и особенно в радиолокации.

ЛБВ

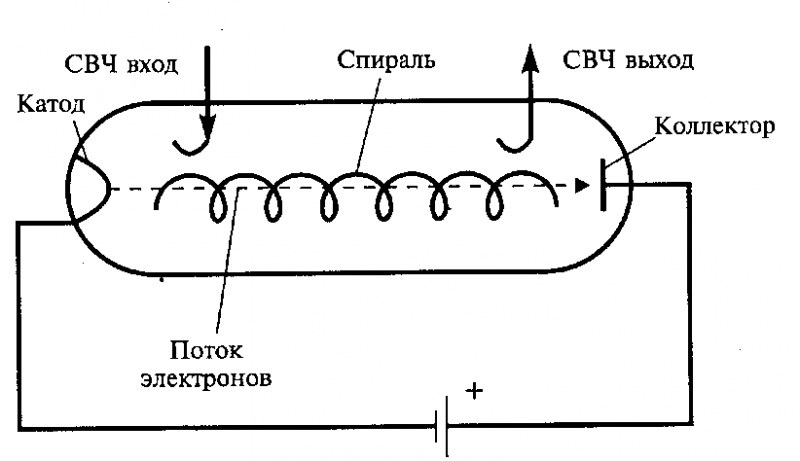
В лампе бегущей волны (ЛБВ) электромагнитная волна со скоростью света движется вокруг специальной спирали - замедляющей структуры, возбуждаемой СВЧ сигналом. Внутри спирали от катода к коллектору движется поток носителей заряда - электронов - со скоростью ,. Фазовая скорость  электромагнитной волны, вектор которой направлен вдоль спирали, на порядок меньше скорости света. Рис. 3.6. При этом добиваются следующего примерного равенства , благодаря чему происходит взаимодействие потока электронов с электромагнитной волной, движущейся в прямом направлении, которая увеличивает свою энергию по мере распространения. Увеличенный по мощности СВЧ сигнал снимается с противоположного от входа конца спирали. Существует несколько разновидностей ЛБВ, в том числе и такие, в которых взаимодействие потока электронов происходит не с прямой, а с обратной электромагнитной волной. Подобные приборы называются лампами с обратной волной (ЛОВ). В ЛБВ и ЛОВ имеет место длительное, непрерывное взаимодействие потока с полем и относительно большое время пролета носителей  от катода к коллектору. Поэтому у этих приборов, как и у клистрона, значение параметра . Анализ работы различных электронных приборов позволяет выделить общие черты, свойственные всем типам ВЧ и СВЧ генераторов.   Схема логарифмирования на операционном усилителе.

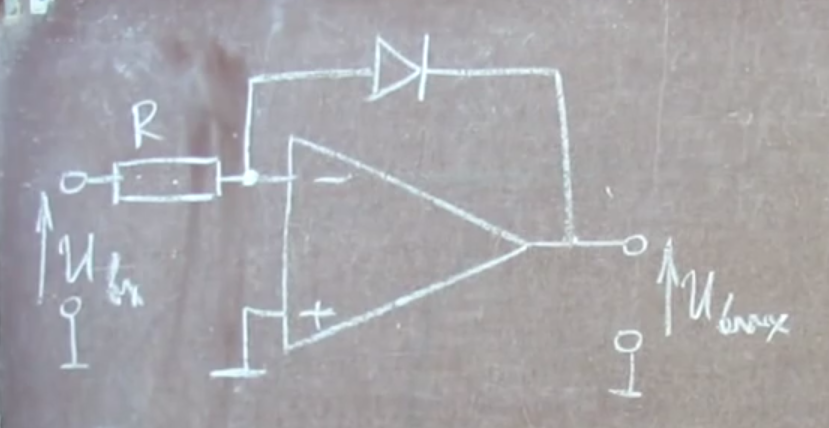
Рассмотрим диод

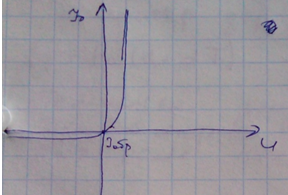
Нас интересует первая четверть.

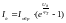
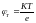, е-заряд электрона

где ϕ_T -тепловой потенциал (const)

если U_д >> ϕ_T , то формула принимает вид

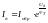
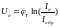
1)Пусть ОУ работает в линейном режиме . (т.е напряжение на входе такое , что операционный усилитель усиливает).

₊-ϕ_-

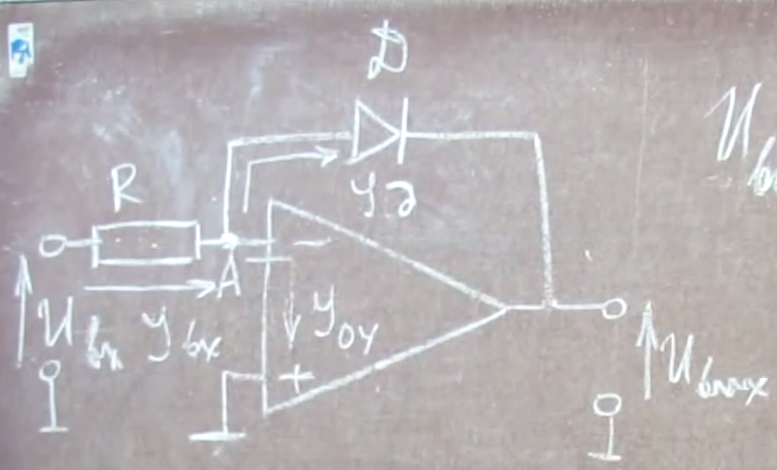
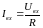
2) Входное сопротивление ОУ велико, где то несколько мега Ом .(в идеале бесконечность)

Напишем закон Кихргофа для точки А.

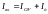. но 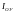(входной ток ОУ) бесконечно мал ,им можно пренебречь.

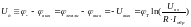
Итого

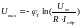т.е напряжение на выходе пропорционально логарифму от входного напряжения.

Билет №19

1. Ряд Котельникова для временной функции.

Теорема Котельникова

Передача непрерывных (аналоговых) сигналов по линии связи предполагает передачу бесконечного множества их мгновенных значений на протяжении конечного промежутка времени. При этом спектр финитного, т.е. ограниченного во времени, непрерывного сигнала бесконечен. Однако, на практике различные радиотехнические устройства (фильтры, усилители и другие) имеют ограниченную полосу пропускания, что приводит к ограничению спектра сигнала некоторой граничной частотой   (или   ), которая определяется свойствами получателя сообщений. Так например, общепринятой нормой в системах передачи речевых сигналов является ограничение спектра сигнала в пределах   , в системах телевидения –   . Как преодолеть противоречие между ограничением спектра сигнала и конечным временем его существования? Ответ на этот вопрос даёт теорема, сформулированная и доказанная академиком В.А. Котельниковым и получившая название теоремы Котельникова или теоремы отсчётов.

Теорема Котельникова формулируется следующим образом. Непрерывный сигнал  , ограниченный по спектру частотой   (или   ), полностью определяется совокупностью мгновенных значений (отсчётов)  в моменты времени  , отстоящие друг от друга на интервал времени     .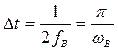

Математически теорема Котельникова определяется выражением

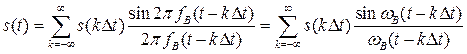 ,         (3.1)

или с учётом (2.12)

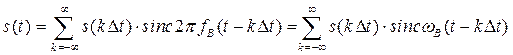 ,     (3.2)

которое представляет собой разложение сигнала   в особого рода ряд по системе базисных функций

 ,

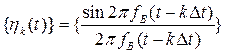являющихся ортогональными на интервале времени   (сравните с разложением сигнала в ряд Фурье).

Доказательство теоремы Котельникова приведено в литературе  [1]. Мы же остановимся на вопросах физического толкования и практического применения результатов теоремы.

Выделим одно из слагаемых ряда (3.1)

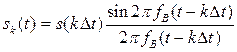 .                            3.3)

Это слагаемое представляет собой отклик идеального фильтра нижних частот (ФНЧ), т.е. фильтра с постоянным коэффициентом передачи в пределах полосы частот от нуля до   , на очень короткий импульс с амплитудой   . (рис. 3.1).

2. О 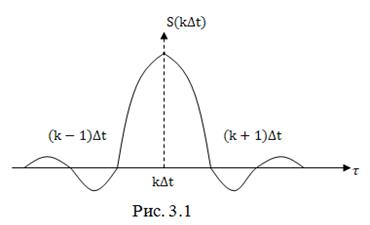тметим, что в моменты времени 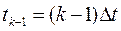  , 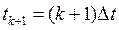  и т.д. значения отклика равны нулю. Это определяет механизм восстановления непрерывного сигнала по его отсчётам.

Формирование последовательности отсчётов непрерывного сигнала, которая представляет собой дискретный сигнал, т.к. значение любого отсчёта   сохраняется неизменным в течение интервала времени   (см. классификацию сигналов), осуществляется при помощи импульсного модулятора.

П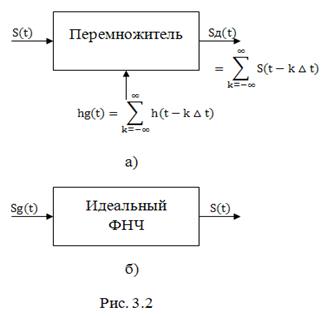 ростейший вариант импульсного модулятора представляет со­бой перемножитель (рис. 3.2), на один вход которого подаётся непре­рывный сигнал   , а на второй – последовательность

коротких единичных импульсов вида (1.13), следующих друг за другом с периодом   (рис. 3.2, а). Тогда на выходе перемножителя будет иметь место последовательность коротких импульсов

 ,

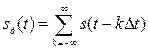а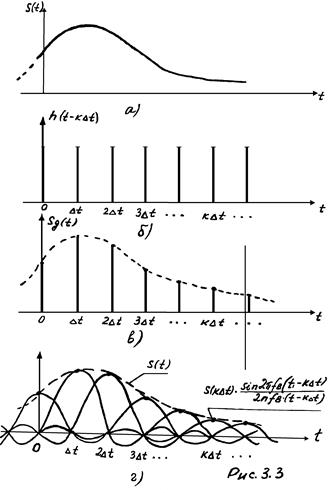 мплитуды которых равны   , т.е. соответствуют мгновенным значениям сигнала   , отсчитанным в момент времени   . (рис 3.3, в).

Процесс формирований последовательности отсчётов называется дискретизацией непрерывного сигнала.

Восстановление непрерывного сигнала осуществляется путём подачи дискретного сигнала   на идеальный фильтр нижних частот. Отклик фильтра на каждый отсчёт определяется выражением (3.2). При этом, в момент времени   , значение отклика определяется только k -тым отсчётом дискретного сигнала; отклик на остальные отсчёты равны нулю (Рис. 3.3, г). Суммируясь, эти отклики дают на выходе ФНЧ исходный сигнал   .

Отметим два важных обстоятельства.

Во-первых, точное восстановление сигнала имеет место только при 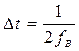  . Введя в рассмотрение частоту дискретизации   , получим так называемую частоту Найквиста, т.е. минимальноезначение частоты дискретизации, при котором возможно точное восстановление непрерывного сигнала. Обычно, на практике частоту дискретизации выбирают выше предела Найквиста. Так, например, частота Найквиста для речевого сигнала при   составляет   . В реальных РТИС эта частота составляет   .

Во-вторых, точное восстановление сигнала возможно при суммировании бесконечного числа откликов, что соответствует сигналу   , неограниченному во времени. Но в действительности, сигналы являются ограниченными и по спектру и по времени. Однако, при определённых допущениях теорема Котельникова справедлива и для этого случая.

Если сигнал, длительностью   ограничивается радиотехническим устройством с граничной частотой  , то для его представления в дискретной форме требуется конечное число   отсчетов, где

 .                               (3.4)

Таким образом для восстановления сигнала длительностью   , ограниченного по спектру частотой   достаточно передать   независимых отсчетов, однозначно связанных с его формой.

Но теоретически сигнал, ограниченный по времени имеет бесконечный спектр. А это означает, что при восстановлении сигнала по   отсчетам будет иметь место ошибка, т.е. восстановленный сигнал ŝ(t) будет отличаться от исходного   . Казалось бы, теорема Котельникова неприменима к реальным сигналам. Тем не менее, если к точности восстановления сигнала   по   отсчетам предъявить определенные требования, например, допустить его восстановление с заданным уровнем ошибки, то утверждения теоремы Котельникова можно с успехом распространить на реальные сигналы, несколько изменив частоту дискретизации по сравнению с пределом Найквиста.

Теперь с учетом того, что реальный сигнал длительностью   представляется   отсчетами мгновенных значений, выражение (3.1) принимает вид:

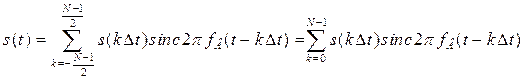 .    (3.5)

Величина   называется базой сигнала   . Понятие базы играет важную роль при представлении непрерывного сигнала конечным числом отсчетов. Соответствующим образом выбранная база определяет информационные показатели сигналов, способность противостоять помехам при передаче по каналам связи, энергетическую скрытность и другие.

Рассмотрим теперь вопрос оценки точности восстановления непрерывного сигнала по совокупности   отсчетов его мгновенных значений. Как уже неоднократно подчеркивалось выше, ограниченный во времени сигнал имеет бесконечный спектр. Согласно равенству Парсеваля (2.50) энергия такого сигнала равна

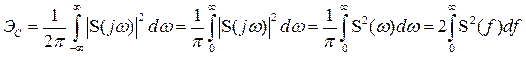 ,    3.6)

где           или   – энергетический спектр, представленный как функция либо круговой   , либо циклической   частоты.

Энергия за пределами частоты   (или   ) составляет величину

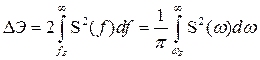 .                        (3.7)

На рис. 3.4 изображен энергетический спектр сигнала, ограниченного во времени и граничная частота   .

Площадь под всей кривой характеризует полную энергию сигнала   , а площадь заштрихованного участка - ту часть энергии   , которая сосредоточена за пределами   .

Т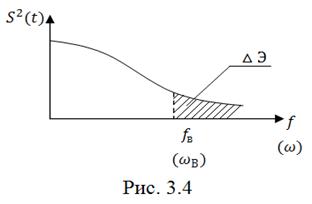 огда отношение

               (3.8)

может  служить  оценкой точности восстановления сигнала. Задаваясь величиной   можно определить частоту   , а следовательно и частоту дискретиза ции   .

Рассмотрим следующий пример. Пусть сигнал   на интервале времени   описывается экспоненциальной функцией

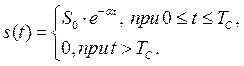
Воспользовавшись преобразованием Фурье, найдем спектральную функцию сигнала

 .

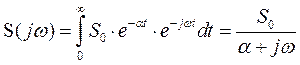Модуль спектральной функции        

 ,

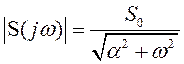а энергетический спектр

 .

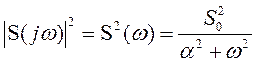Воспользовавшись выражением (3.5), найдем энергию сигнала

 .

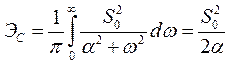В соответствии с (3.6), вычислим   :

 .

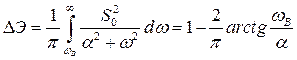При расчете   и   использован табличный интеграл

 .

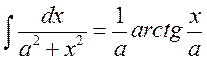Найдем величину среднеквадратичной ошибки восстановления

 .

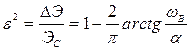Представим

 .

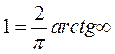Тогда

 ,

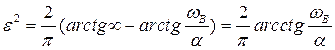откуда следует

 .

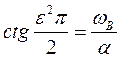Полагая, что для малых значений 

 ,

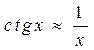получим

 .

Теперь можно найти

 ,

или переходя к циклическим частотам

 .

Частота дискретизации

 .

Таким образом, задаваясь величиной   можно определить частоту дискретизации непрерывного сигнала. Очевидно, число отсчетов при дискретизации рассматриваемого сигнала будет равно

 .

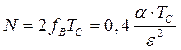Из приведенного примера следует, что чем меньшую ошибку восстановления требуется обеспечить, тем выше должна быть частота дискретизации.

Теорема Котельникова устанавливает однозначное соответствие между аналоговым сигналом и отсчетами его мгновенных значений во временной области. Оказывается, можно сформулировать теорему отсчетов и в частотной области. При этом примем во внимание, что комплексный спектр одиночного сигнала длительностью   является сплошным. Тогда имеет место следующее утверждение. Спектральная функция   сигнала  , ограниченного во времени величиной   полностью определяется совокупностью отсчетов  , отстоящих друг от друга на частотный интервал 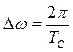  , т.е.

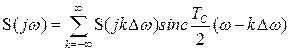 .                     (3.9)

Теорема отсчетов в частотной области основывается на свойстве симметрий преобразований Фурье относительно переменных   (или   ) и   . Суть этого свойства состоит в том, что преобразование Фурье периодического сигнала с периодом   приводит к линейчатой (дискретной) спектральной функции, где отдельные спектральные составляющие (см. подраздел 2.1) отстоят друг от друга по оси частот на величину   (или   ), и наоборот, преобразование Фурье периодической спектральной функции с периодом   приводит к дискретной временной функции с периодом   .

Исходя из этого свойства, если в (3.2) заменить   на   ;   на   , а   на   , то в результате получим выражение (3.9). Как и в случае разложения сигнала   в ряд Котельникова, разложение его спектра ограничивается   отсчетами. Тогда выражение (3.5) в частотной области принимает вид

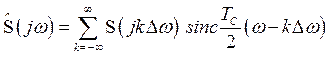 .             (3.10)

Казалось бы, для восстановления спектральной функции   по совокупности отсчетов   , необходимо знать   отсчетов модуля и   отсчетов аргумента комплексных величин   . Однако, если учесть, что модуль спектра   , т.е. амплитудный спектр является четной функцией, а аргумент   , т.е. фазовый спектр – нечетной функцией, то число независимых отсчетов сокращается вдвое и составляет   , т.е. равно базе сигнала.

Подводя итог вышеизложенному, отметим, что теорема Котельникова устанавливает принципиальную возможность представления непрерывного сигнала последовательностью его мгновенных значений. Такую операцию иногда называют импульсным преобразованием непрерывного сигнала. Такое преобразование лежит в основе импульсных методов передачи сообщений в радиотехнических системах. Более того, дискретизация непрерывных сигналов в соответствии с теоремой Котельникова является промежуточной операцией при формировании цифровых сигналов, которые в настоящее время нашли самое широкое распространение как в радиотехнических системах передачи сообщений, так и радиоэлектронных системах обработки, отображения и регистрации информации, и во многих других областях.

2.    Анализ интегрирующей цепи.