Застосування

Будучи доповненою рівняннями перенесення тепла і перенесення маси, а також відповідних масових сил, система рівнянь Нав'є-Стокса може описувати конвекцію, термодифузію в рідинах, поведінку багатокомпонентних сумішей різних рідин і т. п.

Якщо ж у рівняння в якості масової сили ввести силу Лоренца і доповнити систему рівняннями Максвелла для поля в суцільному середовищі, то модель дозволяє описувати явища електрогідродинаміки і магнітогідродинаміки. Зокрема, такі моделі успішно застосовуються при моделюванні поведінки плазми, міжзоряного газу.

Система рівнянь Нав'є-Стокса лежить в основі геофізичної гідродинаміки, в тому числі, застосовується для опису течій в мантії Землі.

Також варіації рівняння Нав'є-Стокса використовуються в динамічній метеорології для опису руху повітряних мас атмосфери, зокрема при формуванні прогнозу погоди. Для опису реальних течій у різних технічних пристроях прийнятну точність чисельного рішення можна отримати лише за такої розрахункової сітці, осередки якої менше самого дрібного вихору. Це вимагає дуже великих витрат розрахункового часу на сучасних комп'ютерах. Тому були створені різні моделі турбулентності, що спрощують розрахунок реальних потоків.

2.3. Гідродинаміка згладжених часток

Гідродинаміка згладжених часток(англ. Smoothed Particle Hydrodynamics, SPH) є широко поширеним дискретним методом вирішення рівнянь Нав'є-Стокса.

Основна маса традиційних і широко відомих алгоритмів SPH в дійсності працюють зі слабо стиснутими рідинами. Такий підхід вимагає дуже невеликого часового кроку, обмеженого числом Куранта, пов'язаним з числом Маха. У ході роботи можливі невеликі помилки розрахунків щільності, які можуть викликати суттєві флуктуації тиску, що може привести до нестійкості чисельного рішення. Уникнути даних проблем можна при використанні абсолютно нестискуваних рідин. Це дозволить збільшити допустиму величину кроку моделювання, і при правильно підібраному розмірі часток, а також ядрі згладжування SPH, описувати в режимі реального часу динаміку рідини на досить великих акваторіях.

Основні труднощі розрахунку потоків в'язкої нестискуваної ​​рідини частково пов'язані з широким діапазоном зміни масштабу турбулентності. Прямий розрахунок повних рівнянь Нав'є-Стокса для тривимірного турбулентного потоку вимагає значних обчислювальних ресурсів. У цьому зв'язку, важливу роль відіграє турбулентна модель, що дозволяє врахувати вплив турбулентності в розрахунках.

Друга складність в розрахунку вузького потоку пов'язана з необхідністю

використання надзвичайно дрібних сіток при розрахунку течії в турбулентному пограничному шарі. Оскільки обчислювальна стійкість існуючих схем рішення безпосередньо пов'язана з розміром мінімальної комірки, то, якщо не приймати досить малий крок за часом, виникають проблеми стійкості розрахунку. В результаті і збільшення роздільної здатності, і зменшення кроку за часом при обчисленнях тягнуть за собою різке збільшення необхідних обчислювальних ресурсів.

Тому для вирішення задач гідродинаміки застосовуються різні підходи, основною метою яких є зменшення обчислювальної вартості методів розв'язання рівнянь Нав'є-Стокса при мінімально можливій втрати точності.  Тому пропонується використовувати метод з використанням осереднених по Рейнольдсу рівнянь Нав'є-Стокса.

У турбулентній течії локальні тиск і складові вектора швидкості змінюються в часі випадковим чином. Основна ідея осереднення полягає в тому, щоб розділити в потоці стаціонарні і випадкові частини.

Згідно підходу Рейнольдса, будь-які миттєві значення гідродинамічних параметрів потоку представляються у вигляді суми осереднених за часом величини та її пульсаційної складової. Фактично це означає, що гідродинамічна величина є випадковою, осереднення якої в часі дає математичне сподівання, а пульсаційна складова – дисперсію випадкової величини.

Слід зазначити, що середнє значення, незважаючи на інтегрування по часу, може змінюватися в часі. Це означає, що період інтегрування повинен бути малим порівняно з характерним часом нестаціонарної зміни величини.

Для опису динаміки рідин більшістю методів використовується модель слабостиснутої рідини, рух якої описується рівняннями Нав'є-Стокса. Система рівнянь Нав'є-Стокса у формі Рейнольдса записується наступним чином:

(1)

(2)

де – ефективна в’язкість.

Величина , де – кінематична в’язкість, – турбулентна в’язкість.

Основним завданням являється визначення коефіцієнта турбулентної в'язкості . На відміну від коефіцієнта молекулярної кінематичної в'язкості , коефіцієнт визначається станом турбулентності і не пов'язаний з властивостями рідини. Він може сильно змінюватися від точки до точки простору залежно від типу течії.

На твердих границях задаються умови «непротікання» і «прилипання» . Початкові умови ставляться в задачах нестаціонарного руху і являють

собою задані в деякий початковий момент часу поля швидкостей і тисків.

Система, складена з рівнянь (1) і (2), замикається на співвідношення між і , які можна отримати з відповідного рівняння стану у формі Тета

де – швидкість звуку в рідкому середовищі,

– щільність середовища в нормальних умовах, для води рівна 1000 кг/м3,

.

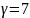Швидкість звуку в рідкому середовищі зазвичай вибирається у багато разів вищою ніж максимальна швидкість потоку рідини, щоб знизити флуктуацію щільності до величини в . Через коефіцієнт ступеня , невеликі флуктуації щільності призводять до великих флуктуацій тиску, але це в загальному випадку не порушує тенденції в русі потоку. Це співвідношення дозволяє зберігати відстані між частинками постійними, за рахунок збільшення сили відштовхування між парами частинок, коли вони наближаються дуже близько один до одного.

Використовуючи явну схему першого порядку, традиційні алгоритми SPH засновані на наступних рівняннях. Швидкість обчислюється як

де – попередній крок ітерації,

– поточний крок ітерації,

Δ – часовий крок.

Позиція і щільність на кожній наступній ітерації обчислюються як

(3)

(4)

 

Якщо вважати рідину абсолютно нестискуваною​​, то використовується окремий випадок рівнянь для стискуваної ​​рідини. Щільність є константою і рівняння (2) виражається:

(5)

Рівняння (1) і (5) утворюють змішану еліптично-параболічну систему щодо невідомих 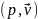. Опис вихрових течій на основі чисельного рішення рівнянь Нав'є-Стокса для нестискуваної ​​рідини супроводжується рядом труднощів. Рівняння нерозривності для нестискуваної ​​рідини містить лише складові швидкості, у зв'язку з чим немає прямого зв'язку з тиском, яка для стискуваних течій визначається через щільність. Внаслідок цього, однією з головних проблем є накладання умови нестискуваності і можливе виникнення нестійкості рішення при накладанні цієї умови.

Іншою проблемою при вирішенні системи рівнянь Нав'є-Стокса є нелінійність, пов'язана з конвективними доданками в рівняннях руху, яка може призводити до появи осциляцій рішення в областях з великими градієнтами.

Для вирішення проблеми використовується метод проекції заснований на принципі розщеплення невідомих. Метод розщеплення по фізичним факторам передбачає поділ системи рівнянь Нав'є-Стокса на послідовність більш простих рівнянь, таких як рівняння дифузії, перенесення і рівняння Пуассона. Розробка чисельних методів для цих рівнянь виявляється значно простішою, ніж безпосередньо для рівнянь Нав'є-Стокса.

Розрахунок поля швидкостей здійснюється в два етапи. На першому етапі обчислюється проміжне поле швидкостей без урахування рівняння нерозривності. На другому етапі здійснюється корекція поля швидкостей, щоб забезпечити виконання рівняння нерозривності. Тим самим здійснюється проекція поля швидкостей на простір векторів з нульовою дивергенцією.

Нехай в момент часу відомі поле швидкостей і поле тиску . Тоді для розрахунку невідомих функцій в момент часу  використовується схема розщеплення, що складається з трьох етапів, а дискретну форму рівняння (1) необхідно розділити на 2 частини.

На першому етапі реалізується попередній крок, де перенесення кількості руху здійснюється тільки за рахунок конвекції і дифузії

(6)

де – проміжне поле швидкості.

Проміжне поле швидкості  не задовольняє рівняння нерозривності, але воно має фізичний зміст, оскільки зберігає вихрові характеристики

На попередньому кроці рівняння (6) може бути переписано як

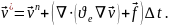
На другому етапі по знайденому проміжному полю швидкості , з урахуванням умови нестискуваності на розраховується поле тиску

(7)

Так як щільність розглядається як постійна величина, рівність (7) може бути переписана як

На третьому етапі реалізується крок корекції, де вважається, що перенесення кількості руху здійснюється тільки за рахунок градієнта тиску

(8)

Проміжне поле швидкості спроектовано без урахування дивергенції, а рівняння Пуассона виводиться за допомогою взяття дивергенції від обох частин рівності (8) і виражається наступним чином

Частки переміщаються тільки з виправленою швидкістю на позиції

визначені виразом (3).