Розділ 2 представлення та методи моделювання течій

2.1. Види потоків рідини і способи їх представлення

Потоки рідини можна класифікувати за двома ознаками: геометричною і часовою. За першою ознакою течії розділяються на наступні типи: просторові чи тривимірні (наприклад, обтікання корпусу судна); плоскі або двовимірні (зокрема, навколо профіля крила); вісесиметричні (наприклад, при русі торпеди); одномірні (зазвичай в трубах).

За часовою ознакою потоки діляться на усталені (стаціонарні – зазвичай при руху течії з постійною швидкістю) і несталі (нестаціонарні – при русі з прискоренням).

Для опису суцільного середовища можливі два підходи: один з них називається лагранжевим, інший - ейлеровим.

Лагранжевий підхід полягає в наступному: у деякий початковий момент часу кожна з рідких частинок «маркується» шляхом присвоєння їй значень координат. Надалі простежується рух кожної частинки індивідуально – шляхом визначення їх траєкторій, тобто координат 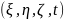щодо початкових значень. Такі координати називають координатами (змінними) Лагранжа.

Вектор положення кожної частинки рідини визначається у вигляді

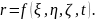
Швидкість і прискорення частинок виражаються через похідні радіус-вектора

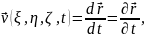
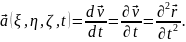
Координати кожної окремої частки в фіксований момент часу є постійними, тому операції диференціювання 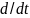і 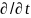тотожні.

Метод Лагранжа зручний при вивченні руху систем, у яких окремі частинки пов'язані одна з одною (тобто відстань між ними не змінюється або змінюється по простих залежностях). У цьому випадку достатньо розглянути рух малої кількості частинок. Застосовується такий підхід при розгляді рухів частинок рідини на границях, наприклад, при вивченні хвильових рухів вільної поверхні.

Усередині області рідини зазвичай рухається велика безліч слабко пов'язаних частинок, простежити траєкторії яких дуже складно. У цих випадках замість методу Лагранжа застосовується метод Ейлера.

Метод Ейлера заснований на вивченні параметрів руху суцільний середовища в кожній фіксованій точці простору з координатами , , 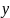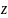в різні моменти часу 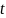. Увага спостерігача фіксується не на самих частинках середовища, а на точках простору, через які вони проходять. Таким чином, до системи координат прив'язані не матеріальні точки (частинки), а характеристики течії середовища (швидкості, прискорення, тиску та ін.). Розподіл будь-якої характеристики в області, яку займає рідина, називають полем.

Поле швидкостей рідини є функцією чотирьох координат Ейлера , , , :

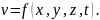
Прискорення визначається у вигляді

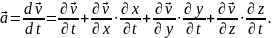
де – локальне (місцеве) прискорення,

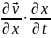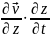, , – конвективное (переносне) прискорення.

Враховуючи, що похідні від координат за часом представляють собою проекції швидкості, конвективное прискорення дорівнює

Якщо місцеве прискорення дорівнює нулю, то залежність швидкості від часу стає неявною, а рух рідини називається сталим (стаціонарним). При цьому конвективное, а значить і повне прискорення в нуль не перетворюється. Цим відрізняється рух легко деформованого рідкого середовища від руху твердого тіла. Якщо конвективное прискорення дорівнює нулю, то поле швидкостей називається однорідним.

При використанні методу Лагранжа визначаються траєкторії – просторові сліди рухомих рідких частинок. В основі методу Ейлера лежать інші характеристики, найважливішими з яких є лінії току.

Лінією току називається крива, до кожної точки якої в даний момент часу дотичний вектор швидкості. При сталому русі лінія току збігається з траєкторією, а при несталому – зазвичай від неї відрізняється.

Наприклад, в біжучої біля поверхні води хвилі частки рідини рухаються по кругових орбітах, радіус яких зменшується у міру віддалення від поверхні (рис. 2.1). Лінії току у хвилі в фіксований момент часу показані на рис. 2.2. На рис. 2.3-2.4 показані фотознімки хвиль на мілкій воді з витримкою, що дорівнює їх періоду. У результаті видно траєкторії руху підфарбованих частинок. У біжучої хвилі траєкторії часток кругові, причому в міру наближення до дна вони стають приплюснутими (рис. 2.3). У стоячій хвилі траєкторії фактично збігаються з лініями току (рис. 2.4).

Для виведення рівнянь ліній току розглянемо частину лінії току нескінченно малої довжини 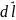, що проходить через початок координат системи . Нехай 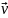– вектор швидкості в центрі цього елемента (за визначенням лінії току він до неї дотичний). Запишемо проекції елемента і вектора швидкості  на осі координат:

 

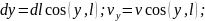
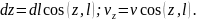
Звідси можна отримати:

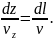
Отже,

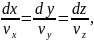
або

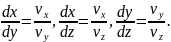(1)

Рівняння (1) і є рівнянням ліній току в диференціальній формі. 

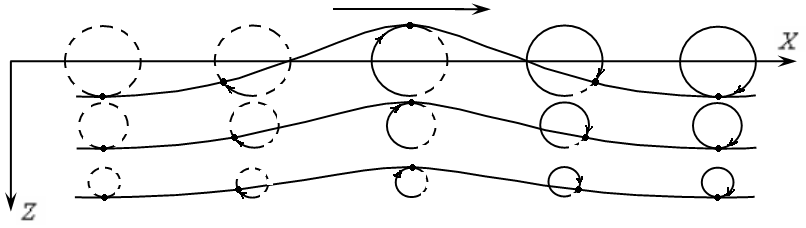
Рис. 2.1 Траєкторія часток рідини під поверхнею хвиль

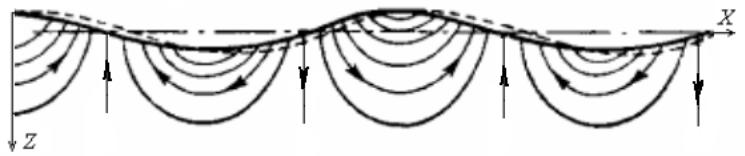
Рис. 2.2 Траєкторія ліній току під поверхнею хвиль

Рис. 2.3 Фотознімок траєкторій частинок біжучої хвилях на мілкій воді

 

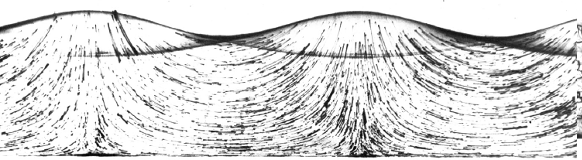
 Рис. 2.4 Фотознімок траєкторій частинок стоячої хвилі на мілкій воді

 

Візьмемо в рідині довільну замкнуту криву, яка не являється лінією току. Через кожну її точку проведемо лінію току. Отримана поверхня називається трубкою току (рис. 2.5). З визначення лінії току випливає властивість трубки току, що полягає у рівності нулю нормальних швидкостей на всій її поверхні. Це означає, що рідина не витікає і не виливається через поверхню трубки. Рідина усередині трубки струму називається рідким струменем. Якщо по будь-якому поперечному перерізі рідкого струменю швидкість не змінюється, то вона називається елементарною.

Через кожну точку рідкого простору можна провести тільки одну лінію току. Проте в деяких точках рідкого простору швидкість може виявитися рівною нулю. У цьому випадку ліві частини в рівняннях (1) стають невизначеними. Отже, через точку з нульовою швидкістю можна провести скільки завгодно ліній струму. Така точка називається особливою (критичною).

 

 

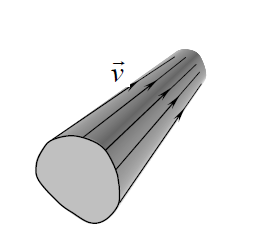
Рис. 2.5 Трубка тока

Рис. 2.6 Лінії току при обтіканні прямокутного виступу

 

Можна подумки уявити також точку, в якій швидкість дорівнює нескінченності. Така точка також є особливою. У ній також повинно спостерігатися сходження нескінченного числа ліній струму. Найпростішим прикладом таких течій є чисто радіальні збіжні і незбіжні течії. Ці течії називаються потоками типу джерело – стік (рис. 2.7).

Рис. 2.7 Стік і джерело

Витратою рідини через задану поверхню 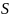називається кількість рідини, що протікає через неї в одиницю часу:

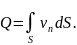
Розмірність об'ємної витрати – .

Крім об'ємної, використовується також поняття вагової витрати рідини, яка являє собою ,

де γ – питома вага.