Аристотелева силлогистика и методы рассуждений

Наиболее часто употребляемые приемы логических рассуждений были впервые охарактеризованы еще аристотелевой логикой и получили название аристотелевых силлогизмов. Создатели известной методической концепции укрупнения дидактических единиц в обучении математике П.М.Эрдниев и Б.П.Эрдниев так характеризуют роль аристотелевской силлогистики в школьном математическом образовании: "В настоящее время образцом логической строгости в школе выступает аристотелева силлогистика: незыблемым считается порядок, когда из двух посылок (большой и малой) выводится одно заключение".

Итак, расклассифицировав описанным в предыдущей лекции образом простые высказывания на типы , Аристотель приступает к анализу умозаключений, которые можно осуществить на их основе. Он выделяет важнейший вид дедуктивных Умозаключений — так называемые силлогистические умозаключения, или силлогизмы. Аристотелев силлогизм представляет собой схему логического вывода (умозаключения), состоящую из трех простых высказываний одного из четырех указанных видов : два первых высказывания — посылки, третье — заключение.

Более точно, умозаключения аристотелевой силлогистики имеют следующее строение. В них рассматриваются три свойства (Аристотель называет их терминами): . Первая посылка (называемая большая) представляет собой простое высказывание, связывающее и ; вторая посылка (называемая малая) связывает и ; следствие связывает и , причем в следствии всегда выступает в качестве субъекта, а — в качестве предиката. Фактически аристотелевский силлогизм есть установление соотношения между двумя свойствами и посредством "связующего" свойства . В зависимости от расположения "связующего" свойства может быть четыре вида силлогизмов (по Аристотелю — четыре фигуры модусов силлогизмов), которые схематически представляются следующим образом (запись в столбец означает, что суждение, записанное под чертой, является следствием суждений, записанных над чертой):

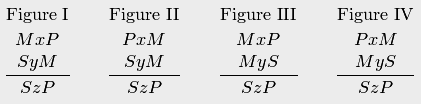
Здесь и запись (как и и и т. п.) обозначает в зависимости от значения одно из четырех суждений видов , включающих соответствующие предикаты и . Поскольку каждое из трех суждений фигуры независимо одно от другого может иметь один из четырех видов, то каждая фигура доставляет следующее количество силлогизмов (схем): . Поскольку фигур 4, то получаем силлогизмов. (Выпишите самостоятельно все силлогизмы каждой из четырех фигур.)

Задача аристотелевой силлогистики, блестяще решенная самим Аристотелем, состоит в том, чтобы обнаружить все те силлогизмы (схемы умозаключений), которые справедливы, т.е. представляют собой логические следования. Таких силлогизмов, как установил Аристотель, имеется ровно 19, остальные — неверны. При этом 4 из 19 правильных силлогизмов оказываются условно правильными.

Для облегчения запоминания всех правильных силлогизмов (или модусов, как их называют) в XIII в. было составлено особое мнемоническое латинское стихотворение. При этом название силлогизма само по себе непереводимо, но дано так, чтобы из гласных букв в него входили лишь те три буквы из , которые указывают на характер посылок и следствия данного силлогизма. Выпишем все верные модусы с их латинскими названиями:

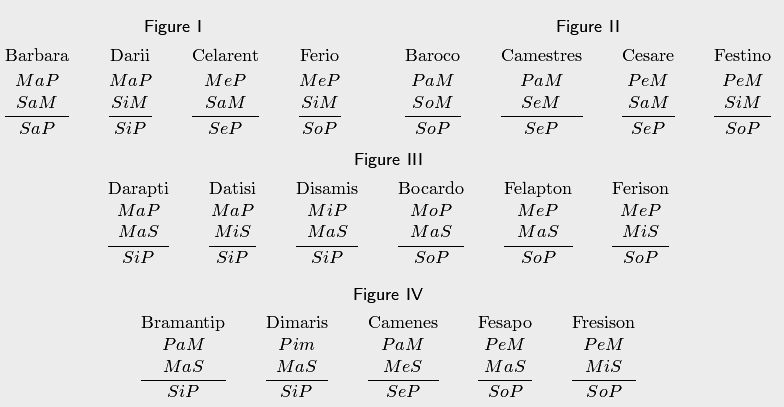
В предыдущем пункте было показано, как на языке логики предикатов каждое из категорических суждений может быть представлено формулой логики предикатов (см. записи (1), (2), (3), (4)). Тогда каждый из 19 правильных аристотелевых силлогизмов также может быть представлен некоторой формулой логики предикатов. Рассмотрим примеры некоторых силлогизмов и дадим их обоснование методами логики предикатов.

Пример 24.6. Самый распространенный и простой силлогизм Barbara: