Частноутвердительное суждение

"Некоторые суть ". Примерами математических утверждений с такими строениями служат следующие: "Некоторые гомотетии суть движения", "Некоторые функции — периодические", "Некоторые параллелограммы могут быть вписаны в окружность", "Некоторые простые числа четны". Приведем примеры нематематических суждений, имеющих такое строение: "Некоторые люди взошли на Эверест", "Некоторые змеи ядовиты" и т.д.

Частноутвердительному суждению придается следующий смысл: существует такой объект , обладающий свойством , который также обладает и свойством . Тогда ему соответствует следующая формула логики предикатов:

(Напомним, что это утверждение представляет собой развернутую запись ограниченного квантора существования.)

Снова, используя технику логики предикатов, можем представить данное суждение в несколько ином виде с использованием квантора общности:

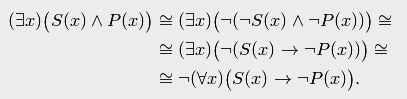
Сравнив теперь общеотрицательное суждение и частноутвердительное суждение , видим, что каждое из них является отрицанием другого.

Частноутвердительное суждение можно выразить на теоретико-множественном языке следующим образом: , где и — множества таких объектов , которые удовлетворяют предикатам и соответственно.

Отметим, что в повседневной речи слово "некоторые" в частноутвердительных суждениях порой опускают, так что, например, фраза "Люди взошли на Эверест" обозначает "Некоторые люди взошли на Эверест".

Частноотрицательное суждение

"Некоторые не суть ". Укажем примеры математических утверждений такого вида: "Некоторые треугольники — неравнобедренные", "Некоторые функции — непериодические", "Некоторые преобразования подобия не являются движениями", "Некоторые ромбы нельзя вписать в окружность", "Некоторые группы не абелевы". Вот примеры нематематических суждений, имеющих частноотрицательный характер: "Некоторые грибы не съедобны", "Некоторые реки не впадают в моря" и т.д.

Частноотрицательное суждение "Некоторые не суть " понимается так: существует такой объект , который обладает свойством ( истинно) и не обладает свойством ( ложно, т.е. истинно ). На языке логики предикатов это записывается следующим образом:

Выражение можно записать в виде ограниченного квантора существования .

Преобразовав его равносильным образом, получаем

Эта равносильность показывает, что общеутвердительное суждение и частноотрицательное суждение являются взаимными отрицаниями.

Частноотрицательное суждение следующим образом выражается на теоретико-множественном языке: , где — множество объектов , удовлетворяющих предикату (свойству) , a — дополнение множества , состоящего из всех объектов , удовлетворяющих предикату .

В заключение отметим, что общеотрицательное суждение и частноутвердительное суждение допускают обращение. Такой вывод можно сделать, если вспомнить выражения для этих суждений на языке логики предикатов с использованием квантора общности и закона коммутативности конъюнкции:

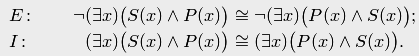
Это означает, что "Никакое не есть " тогда и только тогда, когда "Никакое не есть "" и соответственно "Некоторые суть " истинно тогда и только тогда, когда истинно суждение "Некоторые суть ". Соответствующая запись с кванторами существования для суждений и показывает, что в них буквы и переставить нельзя, эти суждения обращения не допускают.