Общеутвердительное суждение

"Все суть ". Примерами математических теорем, имеющих такое строение, являются следующие: "Все прямоугольники — параллелограммы", "Все гомотетии суть преобразования подобия", "Все дифференцируемые функции непрерывны", "Все поля суть кольца", "Все сферы — тела вращения". Можно указать немало суждений нематематического характера, имеющих такое строение: "Все люди смертны", "Все змеи — пресмыкающиеся", "Все планеты — спутники Солнца".

Суждение "Все суть " в терминах логики предикатов понимается так: каков бы ни был объект , если он обладает свойством (т.е. истинно), то он обладает также свойством (т.е. истинно). Это утверждение на языке логики предикатов выглядит следующим образом:

Логика предикатов дает возможность представить суждение в несколько ином виде с использованием квантора существования. Для этого преобразуем формулу (1) равносильным образом, используя равносильности (получающиеся на основе тавтологий):

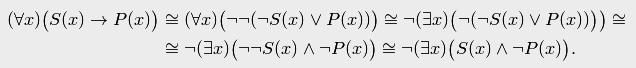
В этом виде суждение можно сформулировать так: "Неверно, что некоторые не суть ".

Отметим, что, как правило, не говорят: "Все суть ", если известно, что объектов, удовлетворяющих свойству , не существует. Обычно под этим суждением мы понимаем следующее: "Существует объект, удовлетворяющий , и все суть ", или в переводе на язык логики предикатов оно выглядит так:

При этом возможно и иное понимание исходного суждения, а именно: "Если существует объект, удовлетворяющий свойству , то все суть , переводимое на язык логики предикатов следующим образом:

Всем этим вариантам предпочтем первый по той главной причине, что данный перевод, во-первых, проще, чем двух других, а во-вторых, при теоретико-множественном толковании суждения "Все суть " он позволяет заключить, что множество всех объектов , удовлетворяющих свойству , является подмножеством множества объектов, удовлетворяющих свойству , то есть .

Отметим также, что в повседневной речи слово "все" в общеутвердительных суждениях порой опускают, так что, например, эквивалентом фразы "Все люди смертны" является вариант "Люди смертны".

Общеотрицательное суждение

"Никакое не есть ". Вот примеры математических теорем, имеющих такое строение: "Никакой эллипс не есть алгебраическая линия первого порядка", "Никакая осевая симметрия на плоскости не есть движение первого рода", "Никакой треугольник не является окружностью", "Никакой числовой ряд, у которого предел общего члена не равен нулю, не сходится". Вот примеры нематематических суждений такого типа: "Никакие змеи не есть птицы", "Никакие камни не разговаривают".

Смысл общеотрицательного суждения: каков бы ни был объект , если он обладает свойством (т.е. истинно), он не обладает свойством (т.е. ложно). На языке логики предикатов это выражается так:

Другими словами, общеотрицательное утверждение читается: "Все суть не ". Можно записать выражение (2) и в виде ограниченного квантора общности: .

Логика предикатов дает возможность представить суждение в несколько ином виде, с использованием квантора существования. Для этого формулу необходимо преобразовать равносильным образом, используя те же равносильности, что и в случае преобразования общеутвердительного суждения:

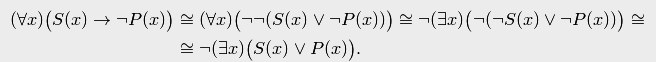
В этом виде суждение формулируется так: "Неверно, что некоторые суть ".

Отметим, что при теоретико-множественном толковании общеотрицательного суждения "Все суть не " запись (2) позволяет заключить, что множество всех объектов , удовлетворяющих свойству , включается в множество всех объектов, не удовлетворяющих свойству , являющееся дополнением множества , то есть .