— "Для любого влечет ".

Пример В.15. Даны высказывания:

= "треугольник является прямоугольным";

= "сумма квадратов двух сторон треугольника равна квадрату третьей стороны";

= "на небе есть тучи";

= "идет дождь".

Методы доказательств теорем

Доказательство математического утверждения, как правило, представляет собой цепочку правильных рассуждений, использующих аксиомы и теоремы, справедливость которых установлена ранее. Рассуждение называется правильным, если из истинности всех посылок следует истинность заключения. Пусть высказывания — посылки, а высказывание — заключение. Рассуждение проводится по схеме , т.е. из предположений следует заключение . Это рассуждение является правильным, если формула тождественно-истинная, т.е. истинна для любых истинностных значений входящих в нее высказываний .

Правильным рассуждениям соответствуют, например, схемы:

— правило вывода (modus ponens);

— правило силлогизма;

— правило контрапозиции.

Во многих задачах нужно доказать справедливость некоторого утверждения (формулы) для любого натурального числа . Непосредственная проверка таких утверждений для каждого значения п невозможна, поскольку множество натуральных чисел бесконечно. Для доказательства таких утверждений (формул) применяется метод математической индукции, суть которого заключается в следующем. Пусть требуется доказать истинность высказывания для всех . Для этого достаточно доказать два утверждения:

1) высказывание истинно для . Эта часть доказательства называется базой индукции;

2) для любого натурального из того, что высказывание истинно для (индукционное предположение) следует, что оно истинно и для следующего числа , т.е. . Эта часть доказательства называется индукционным шагом.

Если пункты 1, 2 доказаны, можно сделать вывод об истинности высказывания для любого натурального .

В самом деле, если высказывание истинно (см. пункт 1), то высказывание тоже истинно (см. пункт 2 при ). Поскольку истинно, то тоже истинно (см. пункт 2 при ) и т.д. Таким образом можно дойти до любого натурального числа , убеждаясь в справедливости .

Замечание В.6. В ряде случаев бывает необходимо доказать справедливость некоторого утверждения не для всех натуральных , а лишь для , т.е. начиная с некоторого фиксированного числа . Тогда метод математической индукции модифицируется следующим образом:

1) база индукции: доказать истинность ;

2) индукционный шаг: доказать для любого фиксированного .

Из пунктов 1, 2 следует, что утверждение верно для всех натуральных .

Пример В.16. Доказать справедливость равенства для любого натурального числа .

Решение. Обозначим сумму первых нечетных чисел через . Требуется доказать утверждение "равенство верно для любого ". Доказательство проведем по индукции.

1) Поскольку , то при равенство верное, т.е. высказывание истинно. База индукции доказана.

2) Пусть — любое натуральное число. Выполним индукционный шаг . Предположив, что утверждение истинно при , т.е. , докажем, что утверждение истинно для следующего натурального числа , то есть . Действительно,

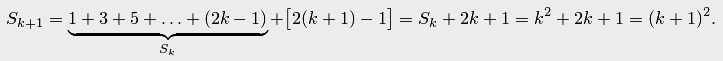
Поэтому и на основании метода математической индукции заключаем, что высказывание истинно для любого натурального , то есть формула верна для любого .

Удаление квантора общности и введение квантора существования

Следующие формулы логики предикатов являются тавтологиями:

а) ; б) .

Закон коммутативности для кванторов

.

Строение математических теорем

Остановимся на формах теорем четырех видов, выделенных еще в аристотелевской логике, основоположником которой был один из наиболее разносторонних мыслителей Древней Греции Аристотель (384–322 гг. до н.э.), и названных категорическими суждениями. Многие математические теоремы имеют именно такой вид. Логика предикатов позволит проанализировать их строение, сравнить между собой, и этот анализ будет более тонким, нежели анализ строения теорем, проведенный в алгебре высказываний. (Впрочем можно заметить, что в алгебре высказываний этот анализ проходил несколько в ином аспекте, и оба анализа скорее дополняют друг друга.)

По Аристотелю, все простые высказывания делятся на следующие шесть типов: единичноутвердительные, единичноотрицательные, общеутвердительные, общеотрицательные, частноутвердительные, частноотрицательные. Первые два типа высказываний есть высказывания о конкретных предметах, последние четыре — о классах предметов.

По традиции, также восходящей к Аристотелю, типы простых высказываний, относящихся к классам предметов, обозначаются гласными буквами латинского алфавита: — общеутвердительные, — общеотрицательные, — частноутвердительные, — частноотрицательные. (Эти буквы соответствуют латинским словам: affirmo — "утверждаю", nego — "отрицаю".) Далее класс предметов обозначается буквой , свойство — буквой . При этом называется субъектом, а — предикатом.

Таким образом, указанные выше четыре типа простых высказываний, относящихся к классам предметов, имеют следующую общелогическую форму:

(общеутвердительное суждение): "Все предметы класса обладают свойством ". ("Все суть ".) Символически: ;

(общеотрицательное суждение): "Ни один предмет класса не обладает свойством ". ("Ни один не есть ".) Символически: ;

(частноутвердительное суждение): "Некоторые предметы класса обладают свойством ". ("Некоторые суть ".) Символически: ;

(частноотрицательное суждение): "Некоторые предметы класса не обладают свойством ". ("Некоторые не суть ".) Символически: .

Исходя из описанного подхода к простым высказываниям анализ их строения состоит в выявлении их субъектно-предикатной структуры, т.е. в выявлении в высказывании субъекта и предиката и фиксировании способа связи между ними (по типу ).

Рассмотрим более подробно эти виды суждений.