О других методах логических рассуждений
Аристотелевская силлогистика охватывает далеко не все типы умозаключений так называемой логики свойств, к которой эту силлогистику принято относить. Полная формализация таких умозаключений осуществляется в логике (одноместных) предикатов. Рассмотрим еще ряд некоторых типов умозаключений.
Пример 24.17. Вот один такой широко распространенный способ рассуждений. Приведем сначала примеры таких рассуждений. "Все люди смертны. Сократ — человек. Следовательно, Сократ смертен". "Всякое нечетное натуральное число является разностью двух квадратов. 7 есть нечетное натуральное число. Следовательно, 7 является разностью двух квадратов". Приведенные рассуждения основаны на следующей схеме:
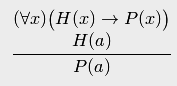
означающей,
что третья формула является логическим
следствием первых двух. Проверим, что
это действительно так. Пусть первые две
формулы превратились в истинные
высказывания
и
при
подстановке вместо предикатных переменных
и
некоторых
конкретных предикатов
и
соответственно,
определенных на некотором множестве
.
Истинность высказывания
означает
тождественную истинность предиката
,
откуда, в частности, вытекает истинность
высказывания
.
Наконец, из истинности высказываний
и
следует
истинность высказывания
,
полученного из заключительной формулы
в
результате подстановки конкретного
предиката
на
место предикатной переменной
.
Тем самым справедливость приведенной
схемы рассуждений доказана.
И аристотелевские силлогизмы, и приведенная схема рассуждений обосновываются с привлечением лишь одноместных предикатов. Приведем пример рассуждения, для обоснования которого уже нельзя обойтись только одноместными предикатами.
Логика предикатов и алгебра множеств
Ранее была показана связь алгебры высказываний с теорией множеств. Логика предикатов усиливает эти связи, так как позволяет дать четкое толкование и обоснование известным теоретико-множественным понятиям и концепциям, а также ввести ряд новых. Например, понятие равенства двух множеств (принцип равнообъемности) на языке логики предикатов выражается так:
а понятие включения множеств следующим образом:
Тогда законы логики предикатов позволяют строго обосновать утверждение.
Пример
24.25.
.
Действительно, доказательство представляет собой цепочку равносильностей:
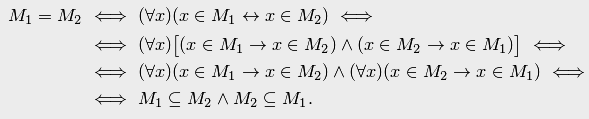
Далее,
тавтологии логики высказываний позволяют
обосновывать свойства теоретико-множественных
операций: дополнения, пересечения,
объединения множеств. При этом каждое
множество
мыслится
как множество истинности одноместного
предиката "
".